FLD1_005 הידרוסטטיקה

→ קודם: FLD1_004הבא: FLD1_006 ←

משוואות וגבול ההידרוסטטיקה

הגבול ההידרוסטטי

נביט במשוואות נאוויה-סטוקס המנורמלות:

נאמר שאנו נמצאים תחת הגבול ההידרוסטטי כאשר:

1. מהירות הזורם קטנה מספיק כך שהאינרציה זניחה:
2. וגם שתהיה קטנה מהשפעות אי-צמיגות:

דוגמה:

מהו סדר גודל מהירות הנוזל המקסימלית עבורה נוכל להניח הידרוסטטיות?
נתון:

פתרון:
צריכים להתקיים שני התנאים. עבור אינרציית הזורם:

הצמיגות:

נסיק שכדי שני התנאים יתקיימו, נצטרך ש:

משוואות ההידרוסטטיקה

תחת הגבול ההידרוסטטי, אנו יכולים להניח שהנוזל נמצא במנוחה. במצב זה, כוחות הגוף, כמו גרביטציה, מאוזנים עם גרדיאנט הלחץ.

משפט:

משוואות ההידרוסטטיקה קובעות כי עבור נוזל תחת הגבול ההידרוסטטי מתקיים:

כאשר הוא גרדיאנט הלחץ; הוא צפיפות הנוזל; הוא התאוצה כתוצאה מכוחות גוף על הנוזל.

פיתוח:
כאשר מתקיימים התנאים להידרוסטטיקה, המשוואה המנורמלת הופכת להיות מהצורה הפשוטה:

מהשוואת מקדמים (הביטוי הימני בכל צד הוא וקטור מנורמל, אז המקדמים חייבים להיות שווים):

עבור השוואת הוקטורים המנורמלים:

לכן, הלא מנורמלים:

חישוב שדה הלחץ ההידרוסטטי תחת כבידה

נוסחה:

כאשר אנו במצב מאמצים הידרוסטטי, וכוח הגוף היחיד שפועל הוא כוח הכבידה, נקבל כי הלחץ נתון ע”י:

כאשר הוא קבוע שניתן למצוא מתנאי שפה.

פיתוח:
כאשר אנו תחת הגבול ההידרוסטטי הידרוסטטי, אנו יודעים שמתקיים:

או, במערכת צירים קרטזית:

זוהי מערכת מד”ח. במקרה שבו הכוח גוף היחיד שפועל הוא כוח הכבידה, אנו יכולים לומר ש:

כאשר הוא תאוצת הכבידה, ובחרנו את כך שהוא פונה כלפי מעלה.
במקרה זה, המערכת מד”ח די פשוטה:

כדי שכל שלושת המשוואות יתקיימו, נשים לב ש:

כלומר, יכל להיות תלוי רק ב-. לפיכך, הוא פשוט קבוע. נסמנו , ונקבל ש:

דוגמה: מיכל מים מעל בריכה

נתון מיכל מים הנמצא מעל פני שטח בריכה (כן, זה אפשרי). נרצה למצוא את הלחץ המינימלי והמקסימלי במיכל, כאשר נתון כי בפני שטח הבריכה, הלחץ הוא לחץ אטמוספרי, גובה המיכל הוא , וצפיפות הנוזל היא .
לפי הנוסחה שמצאנו, נתון ע”י:

נבחר כפני הבריכה. לכן:

לכן:

נסיק שהלחץ יורד ככל שאנו עולים בגובה, ולכן:

משטחים טבולים

נתון משטח טבול מהצורה (עבור דו-ממד). נרצה לחשב את הכוח ההידרוסטטי שפועל על המשטח כתוצאה מלחץ הנוזל, ולפרקו לרכיבים.

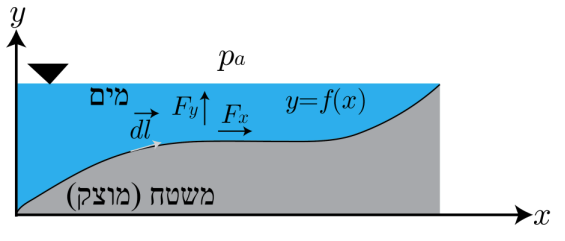
משטח טבול

נסמן ב- את העומק (האורך החוצה מהדף, בכיוון ).
ניתן לרשום:

נבצע את המכפלה הוקטורית עבור :

הכוח ההידרוסטטי הוא סך הלחץ שפועל על המשטח, בכיוון השלילי לנורמל למשטח:

אם אכן העומק אחיד ( אחיד):

אם נפרק לכוח אופקי ואנכי:

נשים לב שבכוח האופקי האינטגרציה מתבצעת לאורך . אפשר לחשוב על זה כך:

פרופיל המשטח

בכיוון האופקי, אנו מעוניינים רק בלחץ האופקי, אבל שנסכם לאורך ציר . באותו אופן עבור הכיוון האנכי.

נוכל להכליל למקרה לאוריינטציה יותר כללית של המשטח:

כאשר את הסימן נקבע לפי הכיוון השלילי לנורמל.

במקרה הכי הכי כללי:

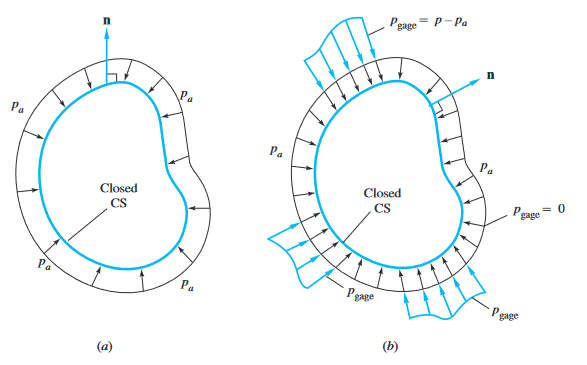
חישוב כוח הלחץ. (a) לחץ אחיד; (b) לחץ לא אחיד.

כלים שלובים

מערכת כלים שלובים היא מערכת בה שניים או יותר כלים מחוברים ע”י צינורות, ומאפשרים לנוזל לזרום בחופשיות ביניהם. בשיווי משקל, סף הנוזל זהה בכל המכלים, בהנחה שהנוזל בלתי דחיס, ואין התנגדות לזרימה.

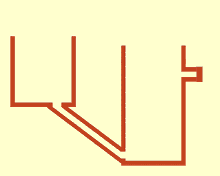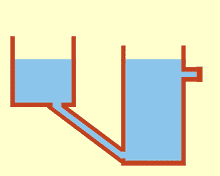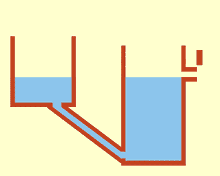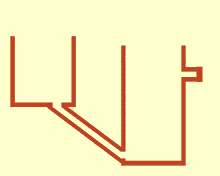
חוק הכלים השלובים.

כאשר המכלים המתקשרים מחוברים מלמעלה, נהוג לקרוא למערכת סיפון (siphon), בהם, למרות כוח הכבידה, המים עולים למעלה דרך הצינור כדי להגיע למצב שיווי משקל.

מיכלים מתקשרים, המחוברים מלמעלה.

נשים לב שבסיפון המוצג באיור, הגבהים של שני המכלים לא שווים - כלומר אנו עדיין לא בשיווי משקל. למעשה, אם נציב את תנאי השפה בפילוג הלחצים של כל מיכל, נקבל לפי חישוב שדה הלחץ ההידרוסטטי תחת כבידה שני קבועי שונים:

נסיק שכאשר הגבהים שונים, לא נוכל באמת להשתמש במשוואות הידרוסטטיקה כדי לחשב את פילוג הלחצים. עוד דרך להסתכל על זה, היא שרק כאשר , אנו תחת ההגבול ההידרוסטטי.

עיקרון ארכימדס

עיקרון ארכימדס קובע שכל גוף, בין אם שקוע כולו או באופן חלקי בנוזל, מרגיש כוח ציפה (buoyant force) השווה למשקל הנוזל שנפחו כנפח הגוף.

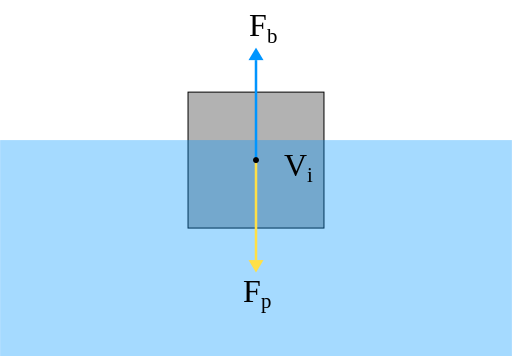
גוף שפועל עליו כוח הכבידה וכוח הציפה .

כוח הציפה פועל על שפת הגוף, והוא למעשה סכימה של הלחצים המופעלים עליו:

כאשר הוא הנורמל החוצה מפני שטח הגוף. לפי משפט גאוס:

לפי חישוב שדה הלחץ ההידרוסטטי תחת כבידה:

נשים לב שאם לא כל הגוף נמצא בתוך הנוזל, ה- הוא למעשה רק נפח הגוף שנמצא ששקע בנוזל. בנוסף, כאן הוא צפיפות הנוזל.
על הגוף כמובן פועל גם כוח הכבידה, שנוכל לרשום כ- . כדי להבדיל בין שני סוגי הנפח, נסמן עבור כל הנפח ו- עבור הנפח ששקוע בנוזל. באותו אופן, כאן הוא צפיפות הגוף, ולכן נבדיל בסימון ע”י עבור הנוזל ו- עבור המוצק.
הגוף צף כאשר יש מאזן בין כוח הכבידה לכוח הציפה:

כעת, בהינתן צפיפות הגוף, הנוזל, ונפח הגוף, אנו יכולים למצוא כמה מהגוף ישקע בתוך הנוזל.

אם יוצא לנו ש- (כמובן שמבחינה פיזית זה לא אפשרי), נסיק שהגוף פשוט שוקע בנוזל. למעשה, נוכל להסיק מכך שכדי לבדוק אם גוף ישקע בנוזל, מספיק לבדוק את ו-:

דוגמה: כדור פורח

נתון כדור פורח במשקל (ללא שום אוויר בתוכו). רוצים לדעת באיזה רדיוס לבנות את הכדור כדי שהכדור “יעוף” (תאכלס, הוא צף מעל האוויר). צפיפות האוויר החם איתו יימלאו את הכדור נתונה כ- , ואילו צפיפות האוויר נתונה כ- .
ניתן להניח שהכדור באמת בצורה כדורית (עם נפח ).
פתרון:
מספיק לבדוק את הקשר בין ו-. ברור ש- לא אחיד, אבל מספיק לחשב את הממוצע שלו:

נבדוק מתי הוא יותר נמוך מ-:

הידרוסטטיקה לא אינרציאלית

לפי משוואות ההידרוסטטיקה:

לפעמים הנוזל שנעבוד איתו לא יהיה במערכת אינרציאלית - כמו למשל משאית מאיצה, או מכל מסתובב. במקרים אלו, עלינו להתייחס במקרים אלו גם לתאוצת המערכת צירים כחלק מהכוחות גוף (אבל בסימן הפוך):

בעצם אנחנו מתייחסים לתאוצת המערכת כ”כוח מדומה”.

למה הסימן הפוך?

בגדול אנחנו די מבצעים פה חטא כשאנחנו במערכת לא אינרציאלית, אבל זה הולך ככה - מתחילים מחוק שני של ניוטון:

ועושים מהלך מתמטי מסובך:

ועכשיו הוא כאילו אחד מהכוחות שלנו, ו- היא התאוצה הנגרמת ממנו.

דוגמה: מערכת מאיצה קווית (משאית)

משאית המכילה נוזל מאיצה בכיוון החיובי של ציר ה-.

משאית מאיצה ימינה

נתייחס גם ל- ככוח גוף, רק בסימן שלילי, ונשתמש במשוואות ההידרוסטטיקה:

כלומר, גרדיאנט הלחץ כרגע פונה בזווית, לעומת מקודם בו הוא פשוט פנה למעלה. נסיק שעכשיו הלחץ ישתנה לא רק בגובה, אלא גם בכיוון . נוכל לרשום את המשוואה כמערכת מד”ח:

באותו אופן כמו בחישוב שדה הלחץ ההידרוסטטי תחת כבידה, נקבל שמכל הקבועים, נקבל רק קבוע שלא תלוי באף קואורדינטה, כך ש:

את נוכל למצוא משיקולי שימור מסה. למשל, נוכל להשוות בין המסה כאשר המערכת במנוחה, וכאשר המערכת מאיצה. פרופיל הנוזל במערכת המואצת יהיה בזווית, לעומת המערכת במנוחה בה הוא פשוט קו אופקי. בכל זאת, המסה בשני המצבים תהיה שווה, ולכן נצטרך רק למצוא את הפרופיל הזה.
אנו יודעים שבשפת הנוזל מתקיים לחץ אטמוספרי . נציב אותו במשוואה:

נקבל משוואת ישר:

ישר זה הוא אוסף כל הנקודות בהן יש לחץ אטמוספרי - המעבר בין הנוזל לאוויר. כעת, מפרופיל זה נוכל לחשב את הנפח של הנוזל, ממנו למצוא את מסת הנוזל, להשוות למסה של המערכת במנוחה, ולחלץ את .

דוגמה: מערכת מאיצה סיבובית

מיכל דק דופן מסתובב בקצב קבוע סביב ציר ה-. המכל מכיל נוזל.

מיכל דק דופן סובב

מתנועה מעגלית קבועה, תאוצת הנוזל כתוצאה מסיבוב המערכת היא . לכן, לפי משוואות הידרוסטטיקה, בקואורדינטות פולאריות :

נשים לב שבפעולת הגרדיאנט יש חשיבות לקואורדינטות בהן אנו עובדים - נושא שאנו לא מרחיבים עליו:

ניתן לחשוב על כך שגרדיאנט הוא מן פעולה הפוכה לאינטגרציה, ולכן לוקחים את ההפוך ליעקוביאן, אבל זה הסבר מאוד לוקה.
נציב במשוואות הידרוסטטיקה ונקבל את המערכת מד”ח:

נקבל ש:

כדי למצוא את פרופיל הנוזל, אנו יכולים למצוא את העקומה (מקודם זה היה ישר, עכשיו זה עקומה) המפרידה בין הנוזל והאוויר ע”י הצבת הלחץ האטמוספרי:

נקבל את הפרבולה:

וכעת נוכל למצוא את משימור מסה (כמו בדוגמת המשאית).

תרגילים

שאלה 1

נתון בול עץ ברדיוס ובאורך אינסופי לתוך הדף. בול העץ נוגע בסכר ושקוע בנוזל בעל צפיפות , כאשר בסביבה שורר לחץ אטמוספרי .

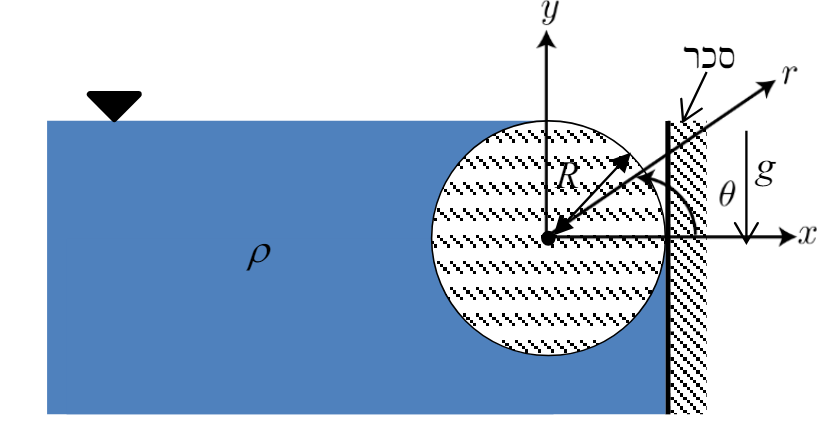
סכימת בול העץ והסכר

סעיף א’

מצאו את פילוג הלחץ שפועל על בול העץ בקואורדינטות פולריות.
פתרון:
נחשב ראשית את שדה הלחץ שלנו (בקואורדינטות קרטזיות). לפי חישוב שדה הלחץ ההידרוסטטי תחת כבידה:

את נוכל למצוא מתנאי השפה ש- . לכן:

נרצה את פילוג הלחץ בקואורדינטות פולריות. לכן:

על בול העץ:

סעיף ב’

מצאו את הכוח ההידרוסטטי האנכי והאופקי שפועל על בול העץ (ליחידת אורך).
פתרון:
הכוח ההידרוסטטי הוא פשוט סך הלחץ. לכן:

כאשר מוגדר בכיוון החוצה מפני המשטח. במקרה שלנו, נצטרך לפרק את האינטגרל לשניים:

כדי לפרק לקואורדינטות קרטזיות (אנכי ואופקי), נשים לב ש:

לכן, בכיוון האופקי:

בכיוון האנכי:

לסיכום:

טיפ:

נשים לב ש- לא מופיע כאן בפתרון. זה לרוב מה שנקבל כאשר אנו מבצעים אינטגרציה על גוף סגור - אז למשל עבור קיר כן היינו מקבלים ביטוי עם .

שאלה 2

גוף בעל צורה פרבולית מוכנס לנוזל, בעל צפיפות , עד לגובה :

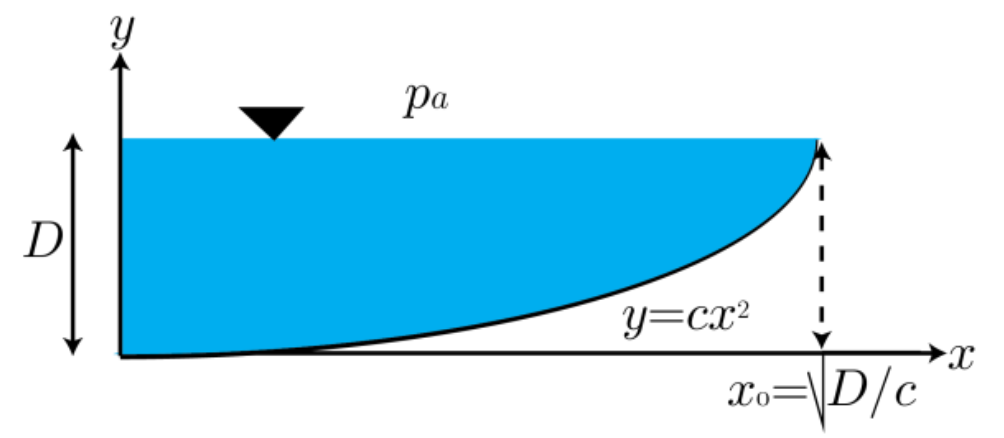
סכימת הגוף

סעיף א’

מצאו את פילוג הלחץ.
פתרון:
לפי חישוב שדה הלחץ ההידרוסטטי תחת כבידה:

בשפת המיכל , ולכן:

סעיף ב’

מצאו את הכוח האופקי והאנכי שנוזל מפעיל על הגוף.
פתרון:
לפי משטחים טבולים:

נציב את הלחץ שלנו:

לכן:

שאלה 3

נתון מיכל מים (בעלי צפיפות ) בעל סימטריה סיבובית, כפי שמוצג בציור. במיכל ממוקמת דלת צירית, בעלת אורך כולל . ציר הדלת נמצא ברדיוס ובעומק ביחס לגובה המים ההתחלתי. ניתן להניח כי רדיוס המיכל גדול ולכן הדלת בקירוב שטוחה. המיכל כולו מסתובב במהירות זוויתית קבועה סביב צירו. לנוחות החישוב, מומלץ להגדיר את מערכת הצירים על ציר הסימטריה, ובגובה פני המים, כמתואר בציור. הניחו שהנוזל נמצא במשטר הידרוסטטי.

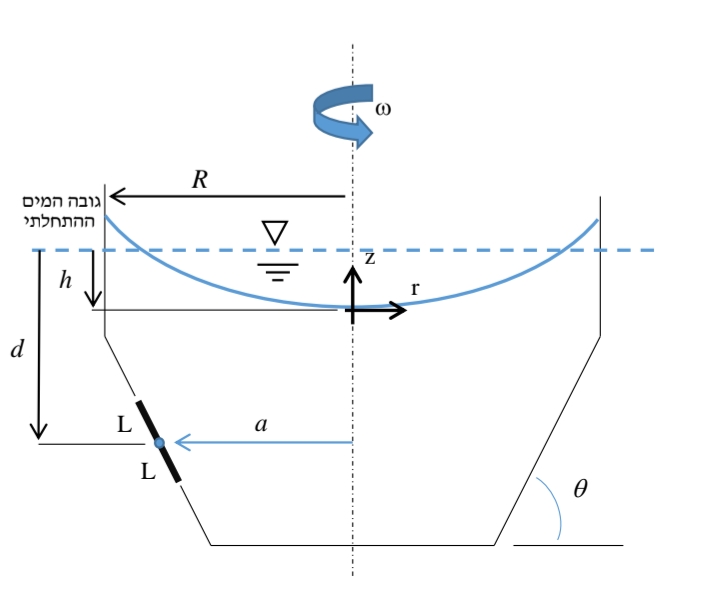
סכימת המיכל המים

סעיף א’

מצאו את פילוג הלחץ במיכל.

פתרון:
לפי הידרוסטטיקה לא אינרציאלית, במקרה של גוף סובב:

נגדיר את מערכת הצירים הפולארית על ציר הסימטריה, ובגובה פני המים (כשהגוף כבר מסתובב!). לכן, , כך שנוכל להפוך את הקבוע שלנו לצורה :

סעיף ב’

אנו יודעים שהלחץ על השפה הוא לחץ אטמוספרי. נמצא את העקומה של השפה - כלומר נמצא מתי :

כלומר, קיבלנו שלשפה יש צורה פרבולית. אנו גם יודעים שזה לא משנה אם המערכת מסתובבת או נחה, ככה או ככה המסה נשמרת:

נתמקד רק במסה שמעל מערכת הצירים שלנו, כי קל לראות שצורת הנוזל מתחת למערכת הצירים לא משתנה. כלומר, נתעסק רק בחלק הגלילי הישר של מכל.
נסמן ב- את גובה המים במנוחה. את קל לחשב - פשוט נפח גלילי:

עבור , נצטרך לבצע אינטגרציה:

נשווה בין שתי המסות ונקבל כי:

סעיף ג’

מה צריכה להיות מהירות הסיבוב כך שלא יפעל מומנט סיבוב על הדלת?

פתרון:
מבחינה אינטואיטיבית, אם הנוזל לא היה מסתובב, הלחץ על החלק התחתון של הדלת היה יותר גדול מהלחץ בחלק העליון של הדלת, ואז היא הייתה נפתחת. סיבוב המיכל יכל לשנות את פילוג הלחצים על הדלת, כך שסך הלחצים על החלק העליון של הדלת יהיה שווה לסך הלחצים על חלקו התחתון של הדלת (בהתחשבות המרחק והציר, ומומנטים וכו’).

אנו רוצים שהמומנט שהכוח ההידרוסטטי מפעיל יתאפס:

כל הכוח באותו הכיוון - הנורמל למשטח קבוע, כך שהאילוץ הופך להיות:

את גודל הכוח נוכל לחשב ע”י האינטגרציה של הלחץ לאורך הדלת :

נשים לב שמפרופיל מיכל המים (שימו לב שוב לאיפה הגדרנו את מערכת הצירים):

נציב, נפתור את האינטגרל, ונשווה לאפס כדי לקבל:

→ קודם: FLD1_004הבא: FLD1_006 ←