CAL2_014 אינטגרלים משטחיים

→ קודם: CAL2_013

משטח

כבר פגשנו משטחים בעבר:
באופן מפורש:

באופן סתום:

באופן פרמטרי:

כאשר נשים לב כי באופן הפרמטרי, זוהי העתקה מ- ל-.

דוגמה:

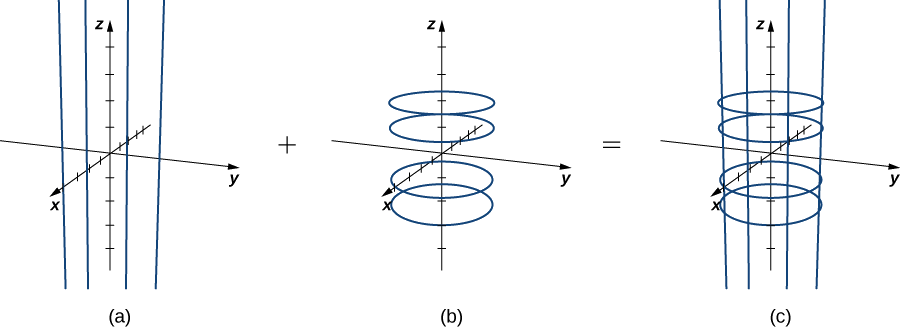
פגשנו כבר קואורדינטות גליליות:

עבור :

כלומר, מצאנו דרך להציג גליל במרחב ע”י שני פרמטרים: ו-.
לכן, המשטח המוגדר ע”י:

כאשר:

מתאר גליל:

דוגמה:

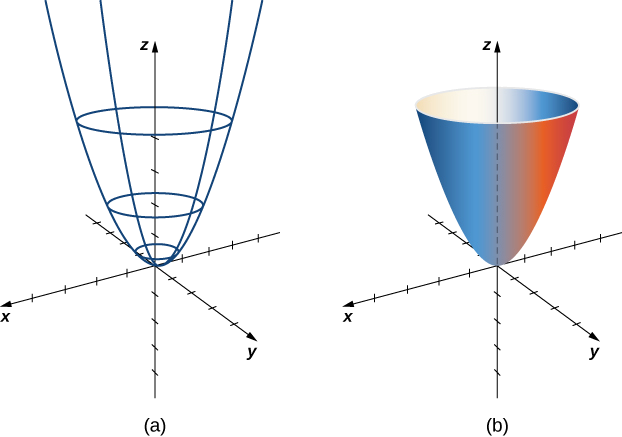
תארו את המשטח הנתון ע”י הפרמטריזציה:

פתרון:
נשים לב כי אם נשאיר את קבוע, אז נקבל עקומה שהיא למעשה מעגל ברדיוס במישור . לכן, ככל ש- גדל, כך גם רדיוס המעגל גדל. אם נשאר קבוע, אז נקבל עקומה שהיא פרבולה אנכית. לכן, נצפה שהמשטח הוא פרבלואיד אליפטי. כדי לוודא זאת, נשים לב כי:

דוגמה:

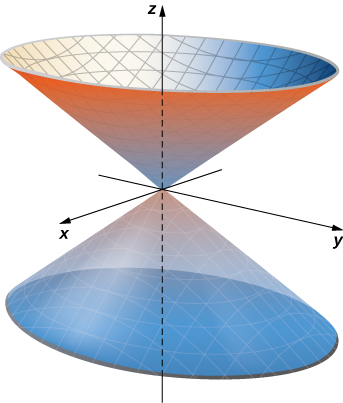
תנו פרמטריזציה לחרוט:

מעל למישור ל-.
פתרון:
החתך האופקי לחרוט בגובה הוא מעגל . לכן, בנקודה על החרוט בגובה יש את הקאורדינטות:

עבור זווית . לכן, הפרמטריזציה היא:

מאחר ולא אכפת לנו משאר החרוט, אלא רק החלק מעל למישור , אז ניתן את הגבולות:

שטח פנים של משטח

יהי משטח בעל פרמטריזציה:

מעל תחום . נניח שהמשטח גזיר ברציפות, כלומר, שכל רכיביו (שהם הפונקציות ) בעל נגזורת חלקיות רציפות. נניח בנוסף ש- הוא מלבן, כאשר בהמשך נוכל להכליל למקרה יותר כללי.

נחלק את לתת-מלבנים בעלי אורכים ו- ו-. נבחר נקודה בפינת כל מלבן. אם נחשוב על כהתאמה בין המישור ל-, אז אפשר לחשוב על הרשת המורכבת מקווים ישרים וניצבים במישור , כמקור לרשת המורכבת מעקומות במרחב .

המשיקים לעקומות הרשת בנקודה הם למעשה נגזרות העקומות בנקודות , כאשר עבור משיק אחד אנו מקבעים את וגוזרים לפי , ובמשיק השני אנו מקבעים את וגוזרים לפי :

באיור הבא הם נתונים ע”י ו-:

עבור מלבנים קטנים מאוד, התמונה של כל מלבן במישור היא מקבילית במרחב , שכיוון צלעותיה נתונות ע”י הוקטורים ו-. מאחר והמלבן המקורי בעל אורכים ו-, המקבילית נפרשת ע”י ו-.
במילים אחרות, אנו מגדילים את וקטורי המשיקים בקבועים ו-, כדי להתאים את הקנה מידה של החילוק לתת-מלבנים המקורי במישור .

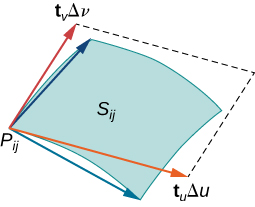
לכן, השטח של המקבילית הוא בערך:

מאחר וגודל המכפלה וקטורית נותנת לנו שטח מקבילית.

הגדרה:

תהי פרמטריזציה חלקה (גזירה ברציפות) וחח”ע של משטח . אזי, שטח הפנים של הוא:

הערות:

1. כדי להקל בהמשך, נעבור לסימון הבא של וקטורים:
   במקום:

נרשום:

דוגמה:

נתון המשטח הבא:

בתחום:

נחשב את שטח הפנים שלו.
נשים לב כי:

המכפלה הוקטורית:

הגודל:

לסיכום:

הערות:

1. אם המשטח הוא מישור אופקי, אז ניתן לתת לו פרמטריזציה:

זו בעצם החלפת משתנים (מוסוות). אנו נקבל כי:

שזהו בעצם היעקוביאן של החלפת משתנים זו:

2. אם נתון ע”י , אז ניתן לבצע את הפרמטריזציה הבאה:

כאשר תחום ההגדרה של . במקרה זה:

גודלו:

ולכן שטח הפנים של הפונקציה הוא:

3. אם נתון ע”י אז לפי משפט הפונקציות הסתומות יש ומתקיים:

ולכן:

ואז שטח הפנים של הוא:

אינגטגרל משטח סקלרי

יהי משטח חלק למקוטעין בעל הפרמטריזציה:

והתחום , ותהי פונקציה סקלרית המוגדרת בתחום שמכיל את . נישאר כעת עם תחום מלבני כאשר לאחר מכן נוכל להכליל לתחומים כלליים.

כמו באינטגרל קווי סקלרי נחלק את התחום שלנו לתת תחומים - תת-מלבנים. נבחר נקודה בכל תת -תחום ונגיע לאותה מסקנה של בניית סכום רימן הבא:

עבור אינטגרל משטחי סקלרי\ אנו נותנים לשטח כל תת-מלבן לשאוף ל-:

אינטגרל משטחי סקלרי

הגדרה:

האינטגרל המשטחי הסקלרי של פונקציה סקלרית מעל תחום חלק למקוטעין מוגדר כ:

חישוב אינטגרל משטחי סקלרי

ההיגיון מאחורי השיטה לחישוב אינטגרל משטחי סקלרי מאוד דומה ל-חישוב אינטגרל קווי סקלרי, ו-שטח פנים של משטח:

משפט:

יהי משטח מעל התחום החלק למקוטעין , בעל הפרמטריזציה:

והפונקציה הרציפה המכילה את התחום . אזי, האינטגרל המשטחי הסקלרי של מעל הוא:

הערות:

1. נשים לב לדמיון הרב לחישוב אינטגרל קווי סקלרי:

דוגמה:

ישנם מספר שימושים פרקטיים לאינטגרלים משטחיים סקלריים. בעזרתם אנו יכולים לחשב את המסה של משטח מסוים בהינתן הפונקציית צפיפות שלו:

ניקח לדוגמה חתיכת מתכת בעלת הצורה של המשטח , מעל המלבן ו-. אם הצפיפות של החתיכת מתכת נתונה ע”י , מהי מסת החתיכה?
פתרון:
יהי המשטח המתאר את הפיסת מתכת. אז המסה שלה נתונה ע”י:

עבור המשטח , נבצע את הפרמטריזציה:

הוקטורים המשיקים:

לכן:

וכעת נוכל לחשב את המסה:

תרגילים:

1. חשבו שטח פני הגוף הכלוא ע”י המשטחים: פתרון:
   אלו הם שני חרוטים הפוכים. עבור החרוט התחתון: חרוט עליון: כאשר שמנו לב שבחיתוך של שני החרוטים: נחשב את של המשטח התחתון: משטח עליון: כעת נוכל לחשב את שטח הפנים של החרוט התחתון: של החרוט העליון: ורק נותר לחבר בינהם.
2. חשבו את השטח פנים של המשטח : פתרון:
   נבודד את : נשים לב כי: ולכן: כעת נוכל לחשב את האינטגרל המשטחי: שזהו כבר אינטגרל כפול שאנו יודעים לפתור ע”י הצבות פולאריות:

אינטגרל משטחי וקטורי

מוטיבציה פיזיקלית: בהינתן שדה וקטורי ומשטח , מהו השטף של דרך משטח ?
למשל, בהינתן שדה מהירויות נוזל, ומשטח , כמה מים עוברים בשנייה דרך המשטח הזה?

כמו באינגטגרל משטח סקלרי, נחלק את לתת תחומים, כך שעבור חילוק גדול מספיק, נקבל מקיביליות קטנות בעלות שטח :

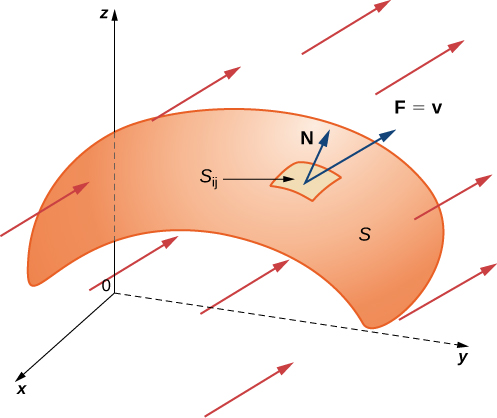
כפי שמצאנו, שטחה הוא:

כאשר הוא הנורמל למשטח בנקודה על המקבילית. ככל שהחילוק יותר גדול, ערך זה נעשה יותר מדויק.

נשים לב כי רק רכיב בכיוון הנורמל למשטח תורם לשטף. לכן, השטף דרך המקבילית הקטנה הוא:

אם נסכום את כל שטפים אילו, בעזרת סכומי רימן ודברים יפים אחרים, נקבל כי השטף דרך הוא:

הגדרה:

האינטגרל המשטחי הוקטורי של השדה הוקטורי מעל תחום חלק למקוטעין מוגדר כ:

כאשר הוא כיוון וקטור הנורמל למשטח. נהוג לקצר ולרשום:

חישוב אינטגרל משטח וקטורי

עבור שדה וקטורי והמשטח בעל הפרמטריזציה:

נשים לב כי המכפלה הסקלרית באינטגרנד נותן לנו פונקציה סקלרית, שעבורה אנו כבר יודעים לחשב אינטגרל משטחי סקלרי:

ולכן, כמו בחישוב אינטגרל קווי וקטורי:

משפט:

יהי שדה וקטורי רציף המכיל את המשטח החלק למקוטעין:

אזי:

הערות:

1. לא תלוי בפרמטריזציה, אבל כן תלוי בכיוון הנורמל:

מבחינה אינטואיבית, כן משנה לנו באיזה כיוון אנו מודדים את שטף המים דרך המשטח. באינטגרל קווי וקטורי, קראנו לכיוון זה [[CAL2_012 אינטגרלים קוויים ומשפט גרין#|מגמת עקומה]]. באינטגרלים קוויים וקטורים קוראים לזה גם מגמה, או אפילו יותר מקובל לקרוא לזה כבר בשם הלועזי למגמה - אוריינטאציה.
2. הרבה פעמים מחשבים את , ורק אז מציבים ב-.

תרגילים:

1. נתונה המקבילית שקודקודיה בנקודות: וכך שוקטור הנורמל ל- יוצר זווית קהה עם ציר החיובי. חשבו את שטף השדה דרך .
   פתרון:
   נמצא פשוט את ע”י מציאת הנורמל למישור. נבדוק אם הנורמל יוצר זווית קהה עם ציר ה- החיובי: לכן הנורמל שמצאנו יוצר זווית חדה. נהפוך אותו כדי לקבל זווית קהה: וכעת נוכל לחשב: כאשר הוא שטח המקבילית.
2. חשבו שטף דרך הצד החיצוני של החרוט הסגור: של השדה: פתרון:
   פרמטריזציה של חרוט: נחשב את : זהו בעל כיוון לא מתאים, מאחר והכיוון החוצה של החרוט הוא בכיוון שלילי של ציר ה-, וקיבלנו כי הכיוון חיובי. לכן נבחר את: לכן (כאן אנחנו לא חייבים לנרמל!): ואת זה לא נחשב כי לרבקה נמאס.
   נותר לנו גם לחשב את המכסה! זהו מעגל, שנבחר עבורו את הפרמטריזציה: לכן, מאחר והנורמל שלו ברור: כאשר הוא שטח המעגל.

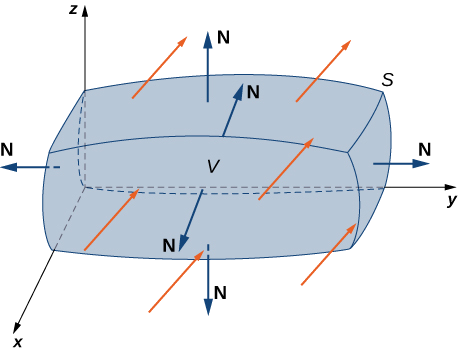
משפט גאוס

לפני שנעסוק במשפט עצמו, נגדיר קודם את הדיבגרנץ.

דיבגרנץ היא פעולה על שדה וקטורי שנותנת לנו סקלר המתאר כיצד השדה מתנהג ככל שמתקרבים או מתרחקים מנקודה.

מקומית, הדיבגרנץ של שדה וקטורי ב- או בנקודה מסוימת נותן לנו מדד ל”כמות ההתפרצות/התכנסות” של שדה וקטורי בנקודה זו.
אם מתאר מהירות של נוזל כלשהו (למשל, נהר), אז הדיבגנץ נותן לנו את הנטייה של הנוזל בנקודה מסוימת “להישפך החוצה”. אם כמות הנוזל שזורמת לתוך שווה לכמות הנוזל שזורמת החוצה ממנה, אז הדיבגרנץ ב- הוא אפס.

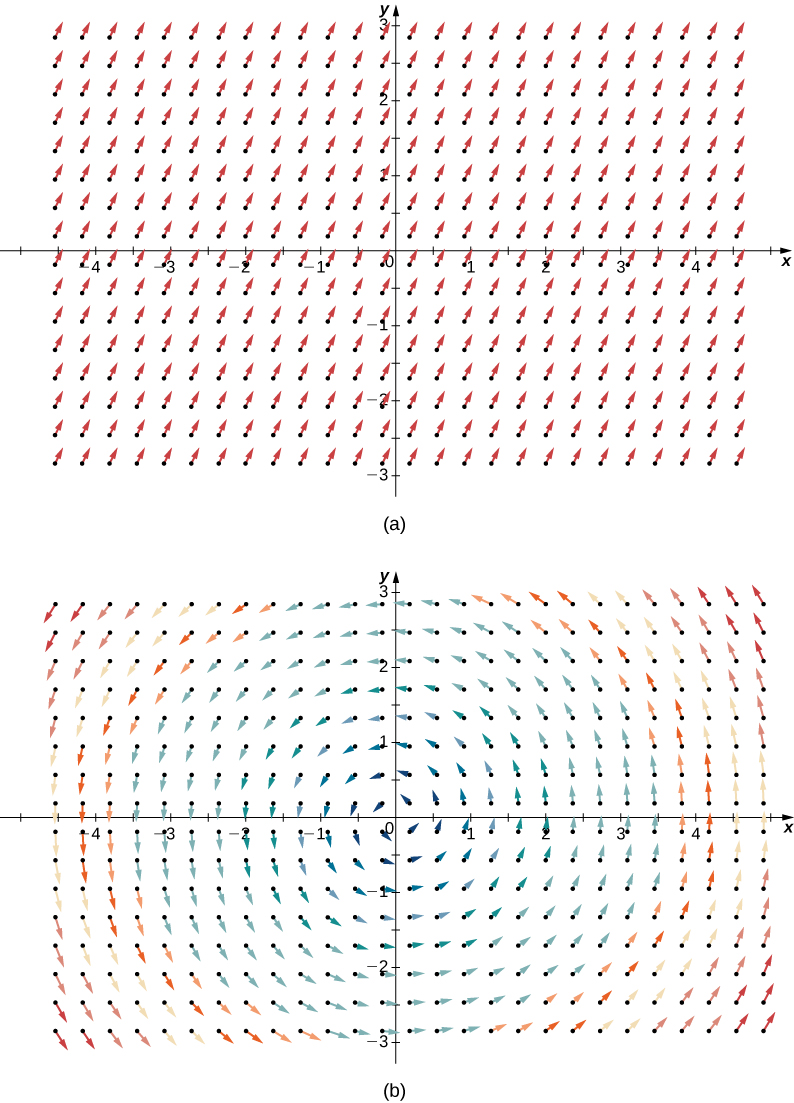
שני שדות בעלות דיבגרנץ אפסי.

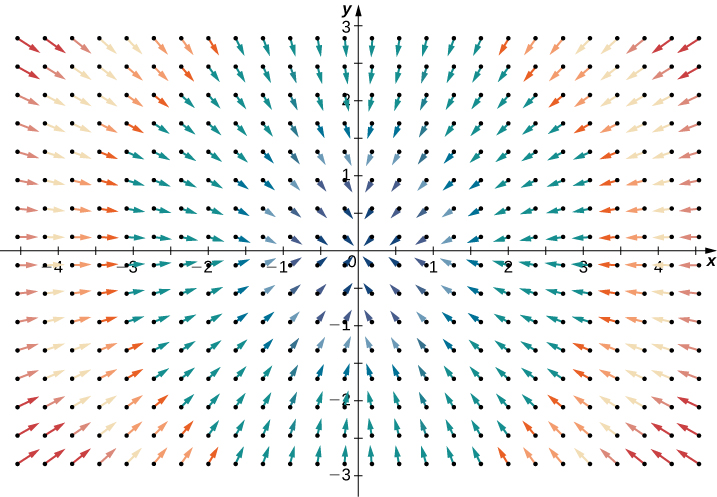
שדה בעל דיבגרנץ שלילי.

דיבגרנץ

הגדרה:

יהי שדה וקטורי ב-, כאשר הנגזרות החלקיות קיימות. אז הדיבגרנץ של מוגדר באופן הבא:

הערות:

1. הדיבגרנץ של שדה וקטורי הוא פונקציה סקלרית.
2. נוכל לרשום את הדיבגרנץ כמכפלה סקלרית של פעולת הגרדיאנט:

והשדה:

זהו פשוט סימון נוח, מאחר והמכפלה הוקטורית של פעולת הגרדיאנט בוקטור לא מוגדרת באמת.
עבור :

3. ישנה הגדרה יותר כללית לדיבגרנץ - אחת שתקפה גם כאשר השדה לא גזיר בנקודה מסוימת. עבור שדה וקטורי , בנקודה , הדיבגרנץ מוגדר כהגבול של היחס בין השטף של דרך משטח סגור בעל נפח הסוגר את , ככל שהנפח שואף לאפס.

כאשר הוא הנפח של ו- הוא שפת .

כמו הגדרת הנגזרת, לרוב לא נשתמש בהגדרה זו של הדיבגרנץ, אלא אם כן מדובר בנקודה לא גזירה.

כדי להמחיש את ההגדרה, נביט בשני שדות וקטורים שהומחשו כבר למעלה:

עבור השדה הוקטורי :

מתקיים:

עבור השדה הוקטורי :

מתקיים:

לעומת זאת, נביט בשדה הוקטורי:

מתקיים:

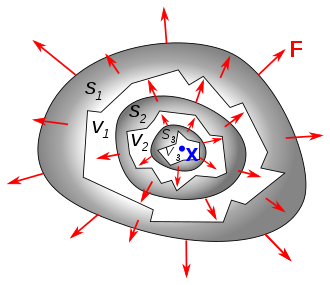
משפט גאוס

משפט:

יהי משטח חלק למקוטעין וסגור (עם נורמל כלפי חוץ) התוחם גוף , ויהי כך ש- בתחום שמכיל את . אזי:

הוכחה?

הערות:

1. למשפט גרין ישנו נוסח נוסף שלא עסקנו בו, שנקרא משפט גרין בנוסח שטף (לעומת נוסח סירקולציה שעבדנו איתו). משפט זה טוען כי:

משפט גאוס הוא למעשה הרחבה של משפט גרין לאינטגרליים משטחיים וקטוריים ואינטגרלים משולשים.
2. משפט זה נקרא גם משפט הדיבגרנץ.

דוגמה:

חשבו את האינטגרל המשטחי:

כאשר הוא הגליל , כולל החלק המעגלי התחתון והעליון, והשדה הוקטורי הוא:

פתרון:
אנו יכולים לחשב את אינטגרל זה בלי משפט גאוס, אבל אז נצטרך לפרק את המשטח לשלושה: הגליל, החלק העליון, החלק התחתון. בנוסף, כל אחד מהם יצטרך פרמטריזציה.
לעומת זאת, בעזרת משפט גאוס, נוכל פשוט לבצע את החישוב הבא:

תרגילים:

1. חשבו שטף של השדה: דרך המשטח הסגור כלפי חוץ: פתרון:
   נפתור ראשית באופן ישיר. שטף דרך גליל: לכן: הוא בכיוון הנכון, מספיק להציב כלשהו ואכן לראות שהוא פונה החוצה מהגליל.
   נחשב: שטף דרך מכסים:
   עוד חישובים שמהם נסיק כי: לעומת זאת, אם נשתמש בגאוס:

משפט סטוקס

הפעולה השנייה שנגדיר על שדות וקטוריים היא פעולת הרוטור, שמודדת את רמת הסיבוב של שדה מסביב לנקודה. נניח כי מתאר את שדה המהירויות של נוזל. אז הרוטור של בנקודה הוא וקטור שמודד את נטיית החלקיקים ליד להסתוב סביב הציר שפונה בכיוון הוקטור.
גודל הוקטור ב- מודד כמה מהר החלקיקים נעים מסביב לציר זה.

במילים אחרות, הרוטור בנקודה הוא מדד ל”סיבוב” של שדה וקטורי בנקודה.

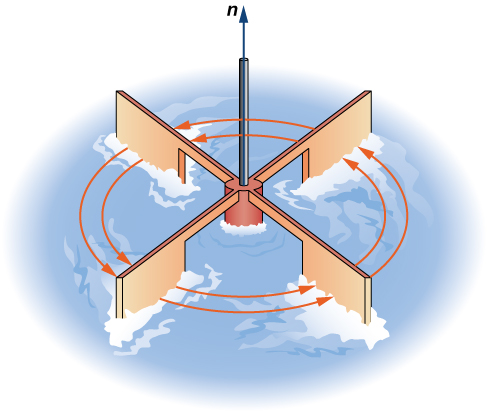
רוטור

הגדרה:

יהי שדה וקטורי בעל נגזרות חלקיות. אז הרוטור ב- מוגדר כ:

הערות:

1. הרוטור נקרא גם קרל (curl).
2. הרוטור נותן שדה וקטורי, לעומת הדיבגרנץ שנותן פונקציה סקלרית.
3. ניתן לזכור את הגדרת הרוטור בעזרת הסימון:

שכמובן זהו לא שימוש לא סטנדרטי בפעולת הגרדיאנט, אבל קל לזכור אותו. מהמכפלה הוקטורית נראה כי:

4. הרוטור של שדה וקטורי :

5. ניתן לרשום את משפט גרין בצורה הבאה:

דוגמה:

מצאו את הרוטור של .
פתרון:
נשים לב ששדה וקטורי זה בנוי מוקטורים שכולם מקבילים. למעשה, כל וקטור בשדה זה מקביל לציר ה-. עובדה זו יכולה להוביל אותנו למסקנה שהרוטור הוא אפס. נחשב:

קיבלנו כי לשדה הוקטורי כן יש סיבוב. כדי להבין מדוע, נדמיין משוטה (הגלגל הזה באיור הקודם) בכל נקודה בשדה.

גדלי הוקטורים בחלקו העליון של הגלגל גדולים יותר מאשר בחלקו התחתון, מה שגורם לו להסתובב. בנוסף, הוא מסתובב עם כיוון השעון - כיוון שלילי, ולכן סימן הרוטור גם כן שלילי.

דיבגרנץ של רוטור מתאפס

משפט:

יהי שדה וקטורי ב-, בעל נגזרות רציפות מסדר שני (כלומר, ). אזי:

מבחן הנגזרות המוצלבות לשדה משמר במרחב

משפט:

יהי שדה וקטורי במרחב על תחום פשוט קשר. אזי אמ”ם שדה משמר.

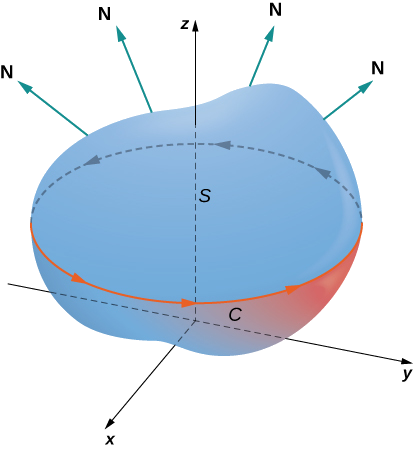
משפט סטוקס

משפט סטוקס אומר כי אנו יכולים לחשב את השטף של רוטור של על משטח , על בסיס אינפורמציה רק על ערכי לאורך הגבול של .
במילים אחרות, אנו יכולים לחשב את האינטגרל הקווי הוקטורי של לאורך גבול משטח , ע”י חישוב אינטגרל משטחי וקטורי של רוטור של מעל .

פרט אחד חשוב: בהנחה וגבול המשטח הוא עקומה פשוטה וסגורה , האוריינטציה (מגמה) של משפיעה על המגמה החיובית של אם, כאשר הולכים על הכיוון החיובי מסביב ל- עם ראשנו בכיוון הנורמל למשטח, , אז המשטח משמאלנו.
דרך יותר פשוטה ניעזרת בכלל יד ימין. כאשר האגודל בכיוון הנורמל, אם עקומת הגבול מסתובבת לפי עיקול האצבעות שלנו, אז נאמר כי חיובית.

משפט:

יהי משטח חלק למקוטעין בעל אוריינטציה, וגבול סגור ופשוט בעל מגמה חיובית. אם הוא שדה וקטורי גזיר ברציפות מסדר ראשון () בתחום פתוח הכולל את , אזי:

הערות:

1. אם הוא משטח אופקי במישור עם נורמל בכיוון החיובי של ציר , אז האינטגרל המשטחי:

הוא למעשה האינטגרל הכפול:

קיבלנו את משפט גאוס:

כלומר, משפט גאוס הוא מקרה פרטי של משפט סטוקס, למשטחים אופקיים.

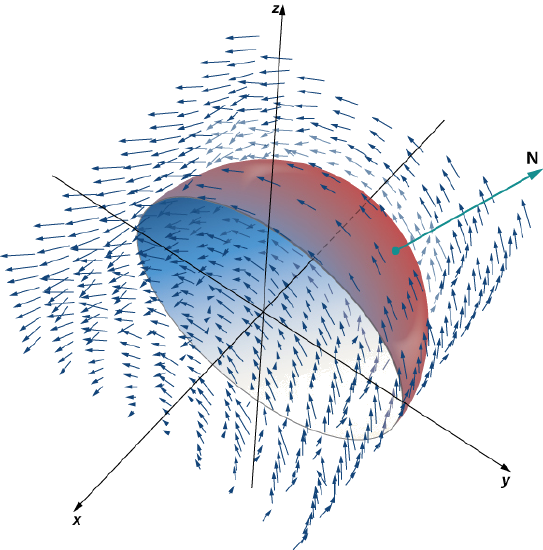
דוגמה:

וודאו שאכן משפט סטוקס עובד עבור שדה וקטורי ומשטח , כאשר הוא חצי כדור בעל אוריינטציה כלפי חוץ, עם הפרמטריזציה .

פתרון:
תהי עקומת הגבול . נשים לב כי הוא פשוט מעגל בעל רדיוס , כאשר מרכזו בראשית, והוא על המישור . למעגל פרמטריזציה . הנוסחה לאינטגרל משטחי:

לפי סטוקס:

→ קודם: CAL2_013