ICT1_012 בקר PID

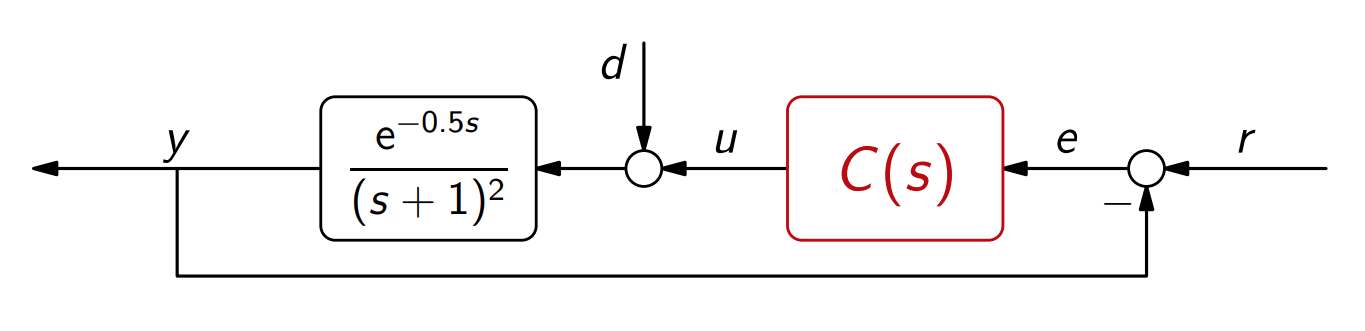
מבוא

ראינו כבר שבקר PI הוא מהצורה:

לפעמים גם רושמים אותו:

כאשר נקרא זמן אתחול.

לעומת זאת, PID הוא בקר מהצורה:

או, באופן יותר כללי (המאפשר גם אפסים מרוכבים):

נוכל כעת לפרט אינטואיטיבית מה כל חלק עושה בבקר PID:

• החלק הפרופורציוני P מתחשב בהווה.
• החלק האינטגרלי I משתמש במידע בעבר.
• החלקי הגוזר D “מנסה” לחזות את העתיד.

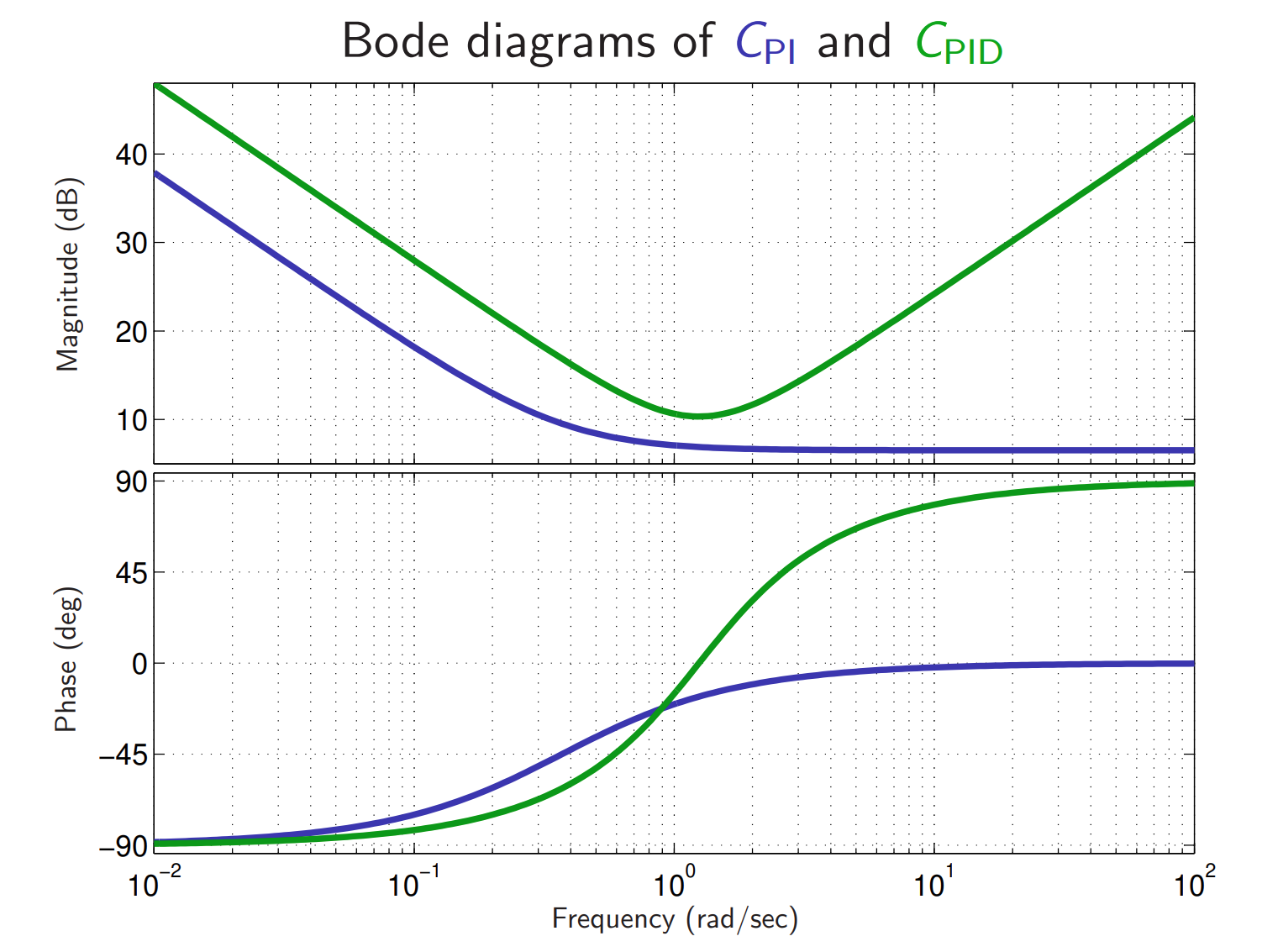
נביט כעת בתגובת התדירות של הבקרים השונים.
עבור בקר PI:

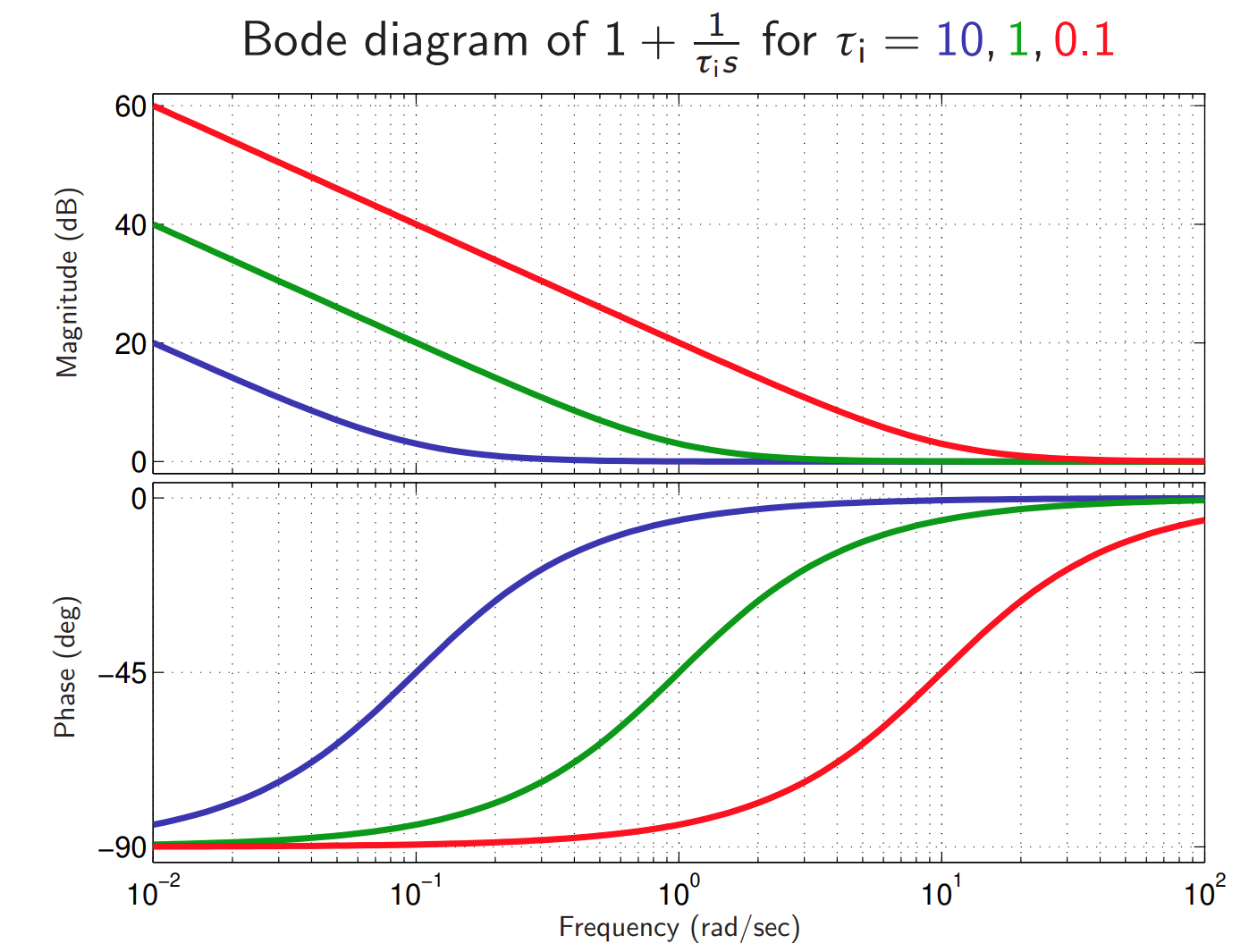
נשים לב שהבקר PI מוסיף פיגור פאזה ולכן מקטין את העודף פאזה. כדי להקטין זאת, נבחר כך ש- .

עבור בקר PD:

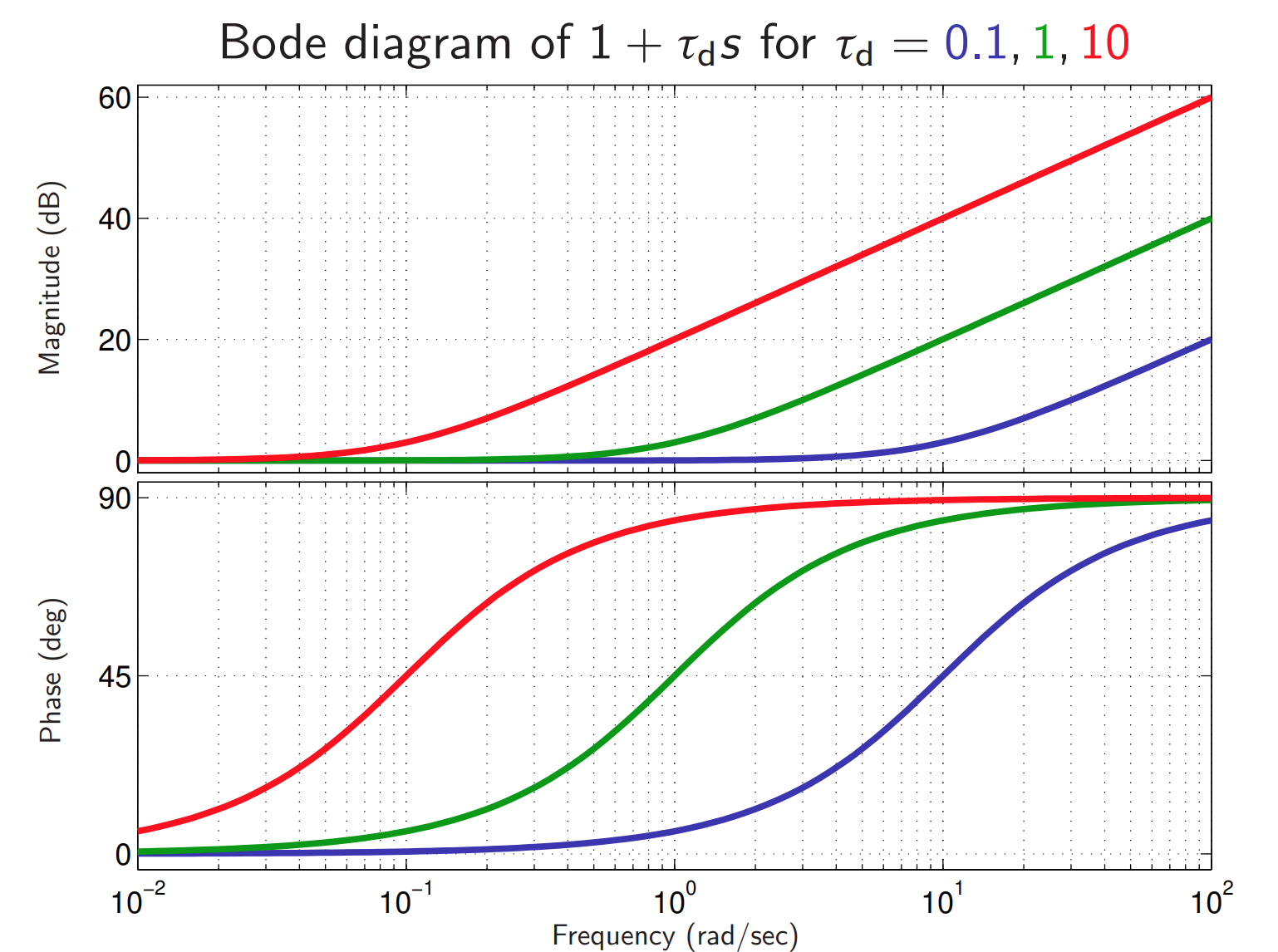
נשים לב שבקר PD מוסיף קידום פאזה ולכן מגדיל את העודף פאזה. כדי לנצל זאת, נבחר כך ש- .

מסקר שנערך ביותר מ-100 תחנות כוח בפרובינציית גוואנג-דונג בסין מצאו ש- מכל הבקרים היו PI, היו PID, ו- השתמשו בבקרה מתקדמת (לא יודע מה זה, נשמע כמו משהו מסובך). הסיבה שפעולת הגזירה בשימוש רק ב- מכל הבקרים היא שהיתרונות של “חזיית” העתיד משמעותיות בעיקר לתהליכים שמאפשרים הגברים גבוהים בבקרים. עבור הרבה מהמערכות, פעולת הגזירה, “חזיית” העתיד, שמתבצעת ע”י אקסטרפולציה לינארית, עלולה ליצור אותות בקרה גדולים ולפיכך לא רצויים בגלל הגברת רעש המדידה. בקרת טמפרטורה היא דוגמה טיפוסית למקרה בו פעולת הגזירה יכולה לעזור: לחיישנים יש רעשי מדידה נמוכים כך שנוכל לתכנן לבקרים הגבר גבוה.

כוונון PID

בתכנון בקר PID אחד מהאתגרים שעומדים לפנינו הוא כוונון הפרמטרים של הבקר. פותחו המון שיטות שונות לאופן כוונון נכון וטוב.

כוונון זיגלר-ניקולס

שיטת הכוונון הראשונה פותחה ע”י זיגלר וניקולס בשנות ה-40 (Ziegler & Nichols, 1942). הרעיון שלהם היה לבצע ניסוי פשוט על התהליך וממנו לחלץ מאפיינים של דינמיקת התהליך במישור הזמן והתדר.
בשיטת מישור התדר, הבקר מחובר לתהליך, מגדירים את הגבר האינטגרטור והגוזר לאפס, ומשחקים עם ההגבר הפרופורציונאלי עד שהמערכת מתחילה לתנוד.

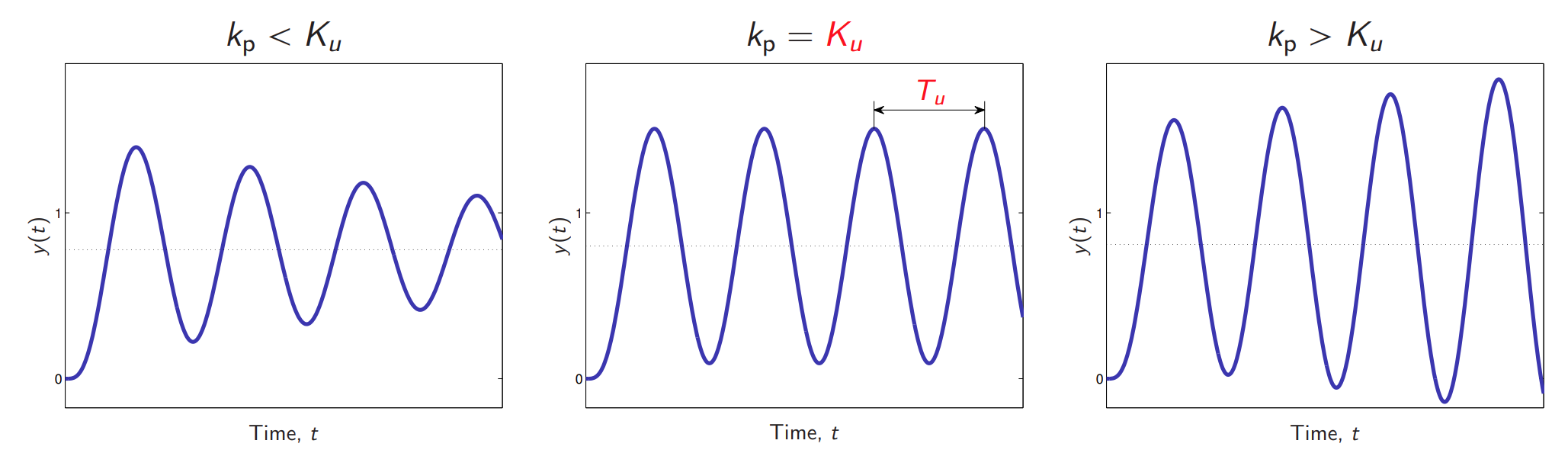
תגובת המערכת לערכי הגבר פרופורציוניים שונים. (Leonid Mirkin’s Homepage, n.d.).

הערך הקריטי של ההגבר הפרופורציוני נמצא ביחד עם זמן המחזור .

הערה:

למען האמת, ו- (כאשר הוא תדר מעבר הפאזה).

בעזרת ערכים אלו, זיגלר וניקולס מציעים את הערכים:

ערכים אלו מוצעים רק כנקודות התחלה. לרוב, נצטרך לשחק עוד עם הפרמטרים כדי לקבל את התוצאה הרצויה.

דוגמה:

עבור החוג הסגור:

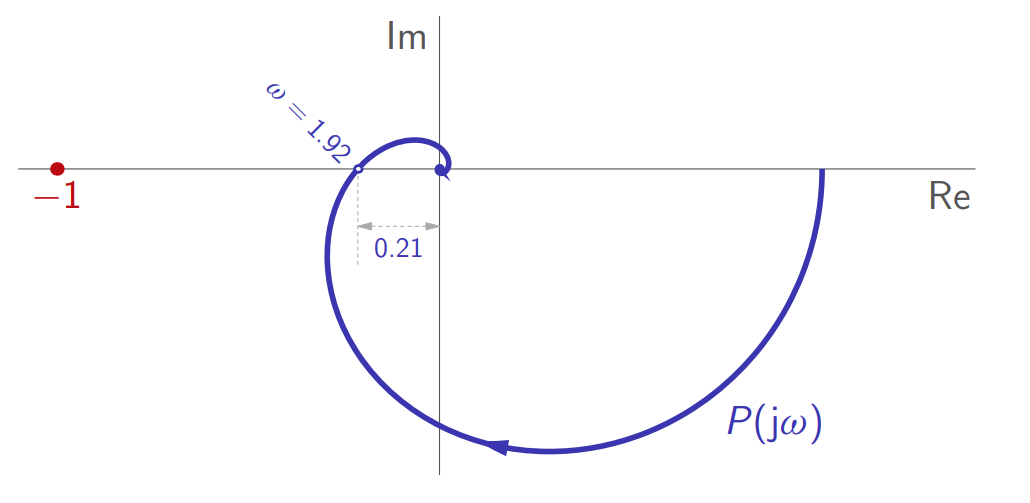
העקום הפולארי של התהליך:

נקבל:

לכן לפי זיגלר-ניקולס נקבל את הבקר PI או הבקר PID:

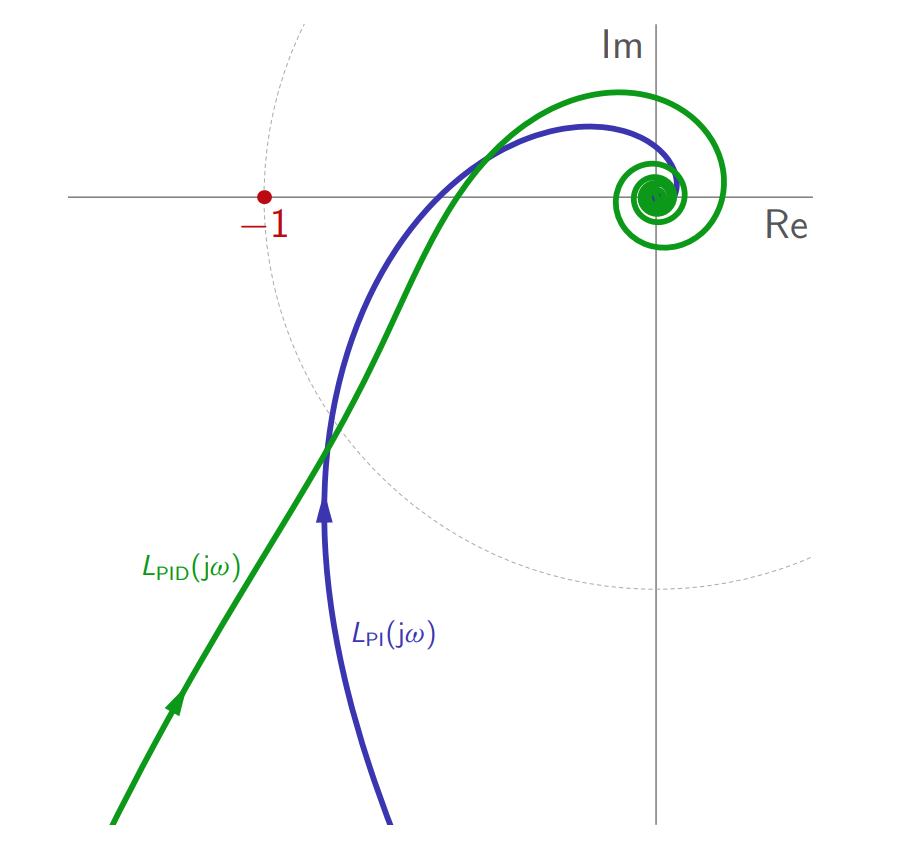
מבחינת הגרף הפולארי:

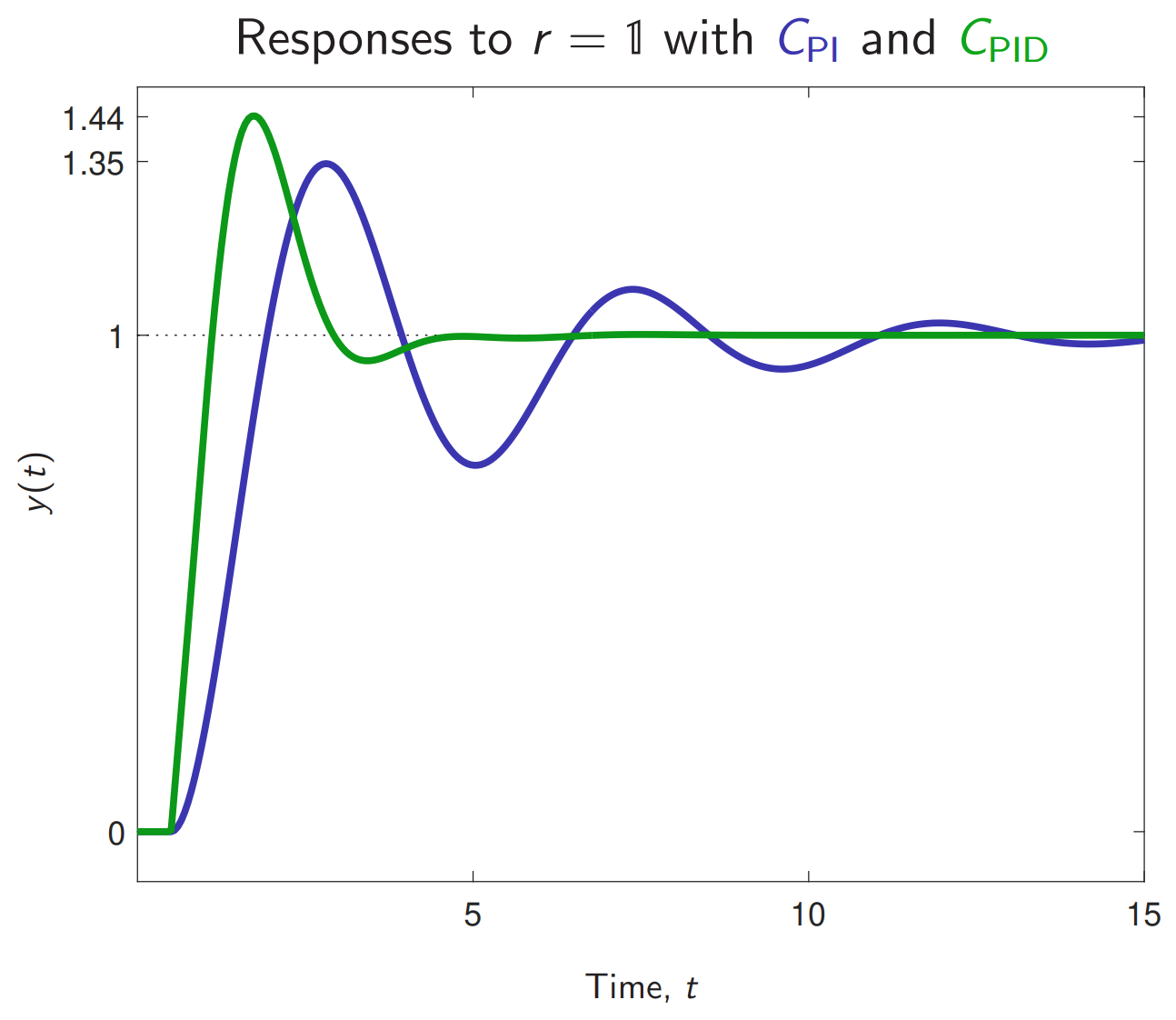
תדר המעבר ועודפי ההגברים והפאזות המתקבלים:

מבחינת התגובות מדרגה:

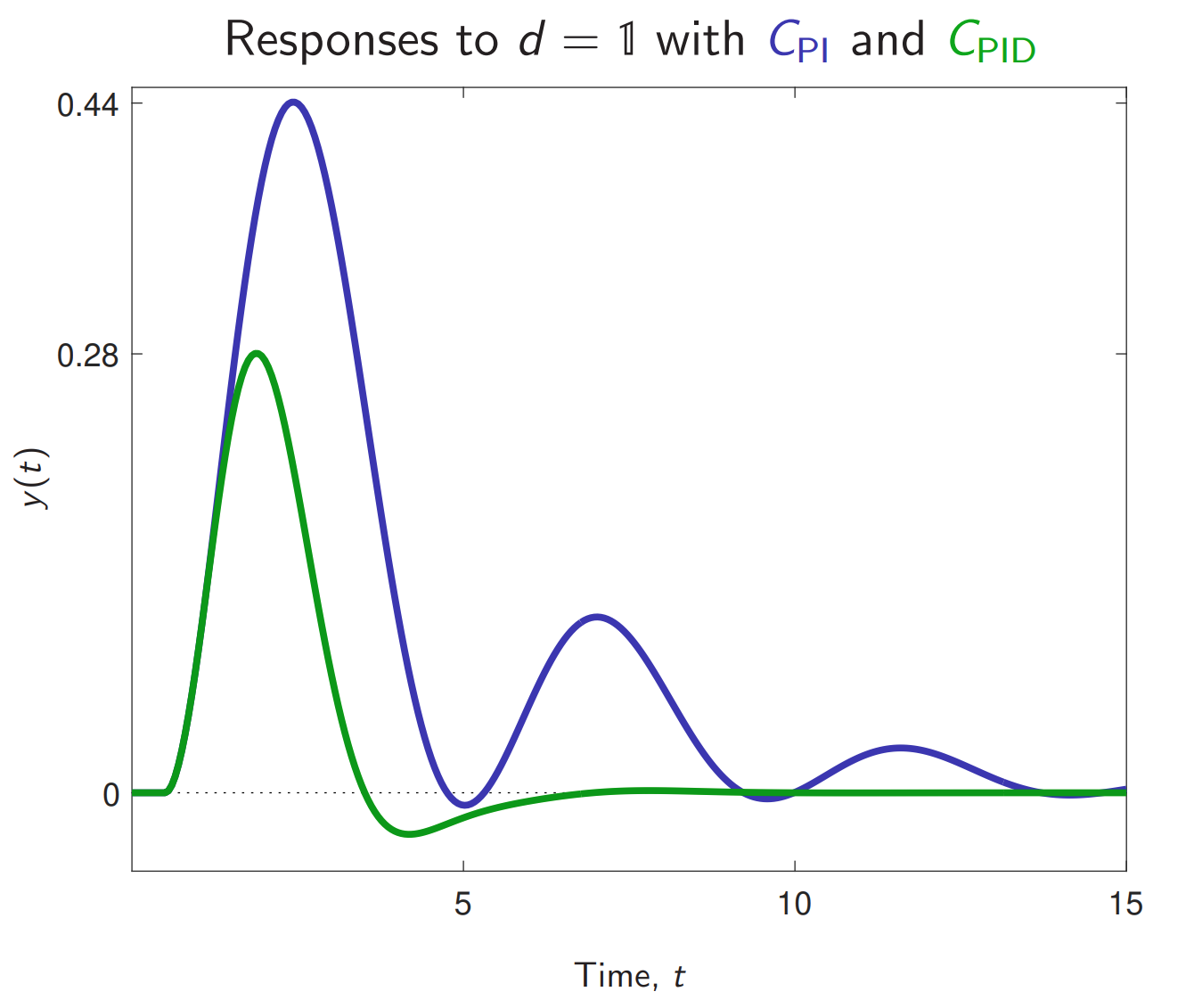
מבחינת התגובות להפרעת מדרגה.

ארכיטקטורות PID

עד כה עסקנו במשוב מסוג משוב יחידה:

אות הבקרה במישור הזמן:

הפונקציית תמסורת של הבקר:

נשים לב שיש לו אפסים. אם נביט בפונקציית תמסורת של המערכת:

נשים לב שהאפסים של הבקר הם גם האפסים של , ואנחנו לא אוהבים אפסים, כי אם הם דומיננטיים מספיק, הם יכולים לגרום לתגובת-יתר () גדולה מדי.

דרך אחת לטפל בבעיה זו היא לשנות את הארכיטקטורה של החוג הסגור:

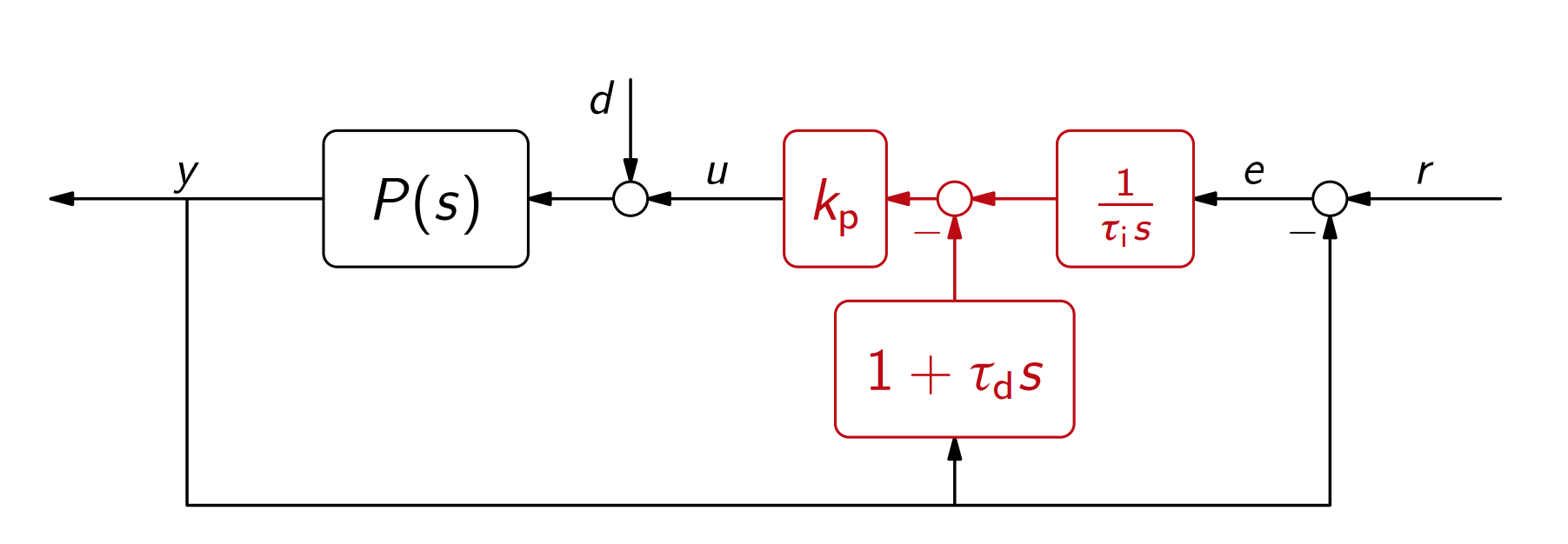
כעת:

כלומר, אנחנו מפעילים את הגזירה, D, רק על היציאה , ולא על כל השגיאה . לפיכך, הגזירה לא תגדיל לנו שינויים משמעותיים בשגיאה, בעוד האינטגרטור, שמטרתו לאפס את השגיאה, עדיין פועל כרגיל על .

פונקציית המערכת היא:

לפונקציית תמסורת זו יש רק את האפסים של התהליך , כך שבאמת כנראה נקבל תגובות מעבר יותר חלקות. באותו הזמן, תגובת ההפרעה לא מושפעת משינוי ארכיטקטורה זה, שזה אחלה.

דוגמה:

בהינתן אותה המערכת מהדוגמה הקודמת:

אז ל-

יש אפס ב- , בעוד-

הוא פונקציית תמסורת מסדר שני ללא אפסים.
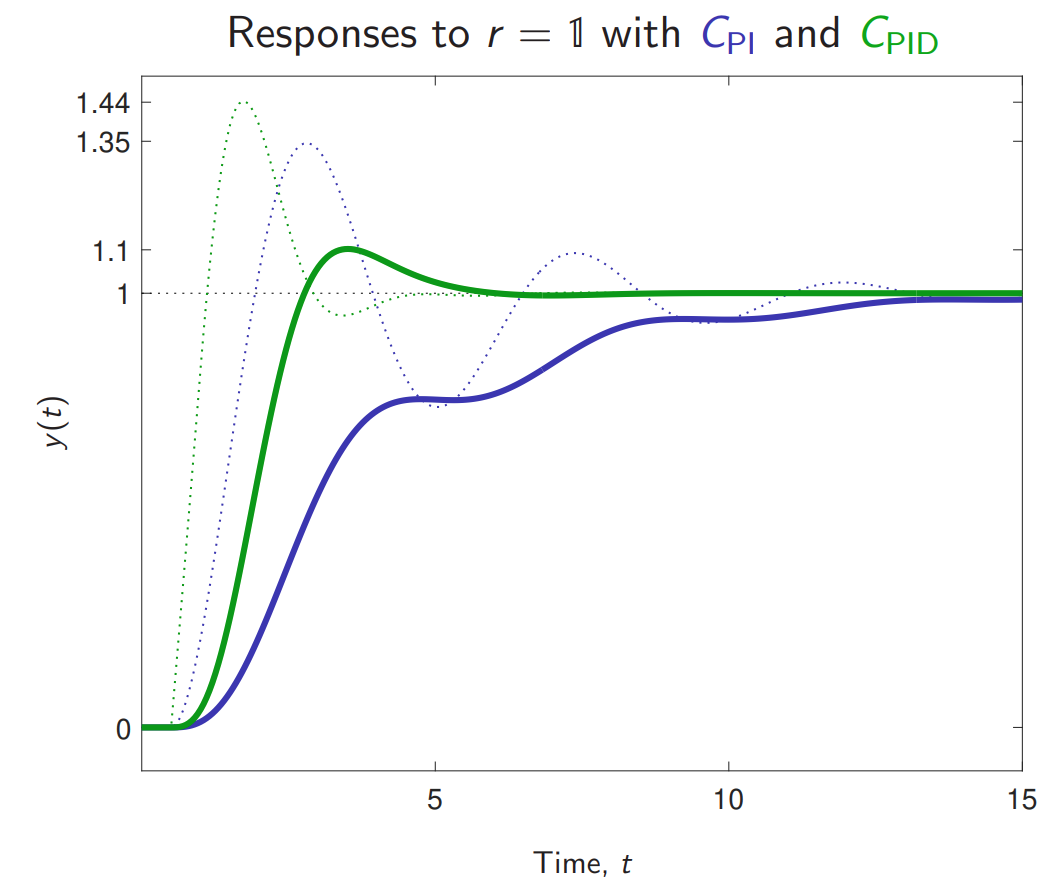
עם אותו הכוונון, אבל בארכיטקטורות שונות, תגובות המדרגה:

בקרה בשתי דרגות חופש

בקרה בשתי דרגות חופש (2DOF controllers) היא סוג של שילוב בין בקרה בחוג פתוח לבקרה בחוג סגור. הרעיון הוא להתעלם מהבקר אם המערכת מתנהגת כרצוי.

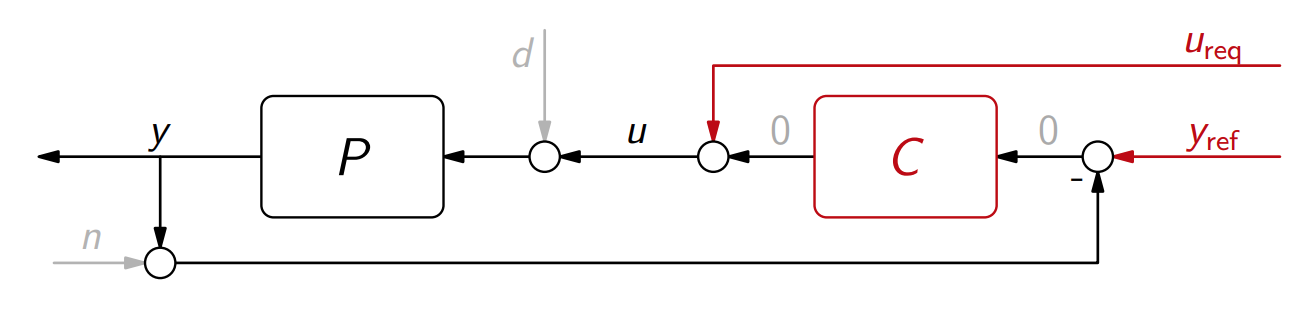
כדי לבטא את ההתנהגות הרצויה, אנו דורשים מהאותות החדשים ש:

1. האותות ו- חסומים (להבטחת יציבות).
2. מתקיים (להבטחת עקביות).

אם , אז ניתן לראות מהדיאגרמה:

נשים לב שיש לנו כבר שמות למקדמים של ו-:

מאחר ו-(לפי משוב יחידה) וגם :

קיבלנו ש- , כך שעם איך שהגדרנו את , נקבל:

כך ש- , בלי תלות ב- (כל עוד מייצב).

אם נבחר וגם עבור , אז:

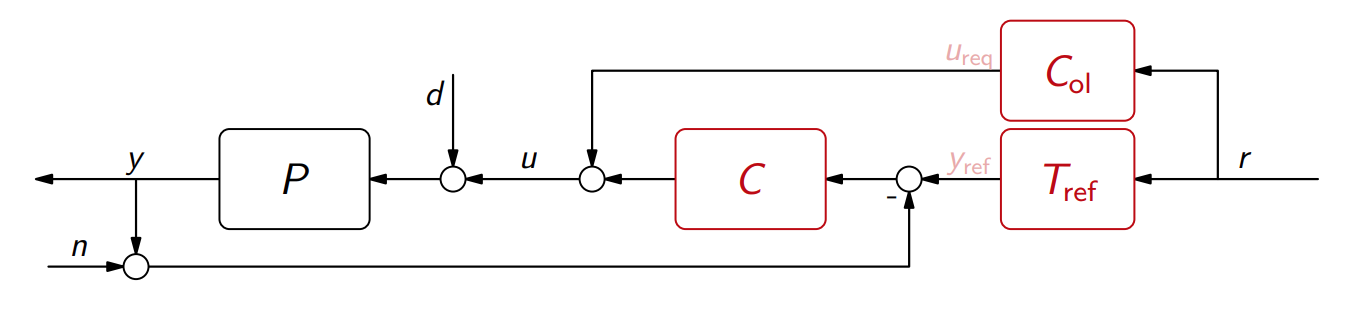
אנו מעוניינים באותות:

בקר זה משלב בקר בחוג סגור ובקר בחוג פתוח עם הפרדה מוחלטת בין התגובה הנומינלית של המערכת (שמאופיין ע”י ) וייצוב וטיפול באי-וודאויות של המערכת (שמאופיין ע”י ).

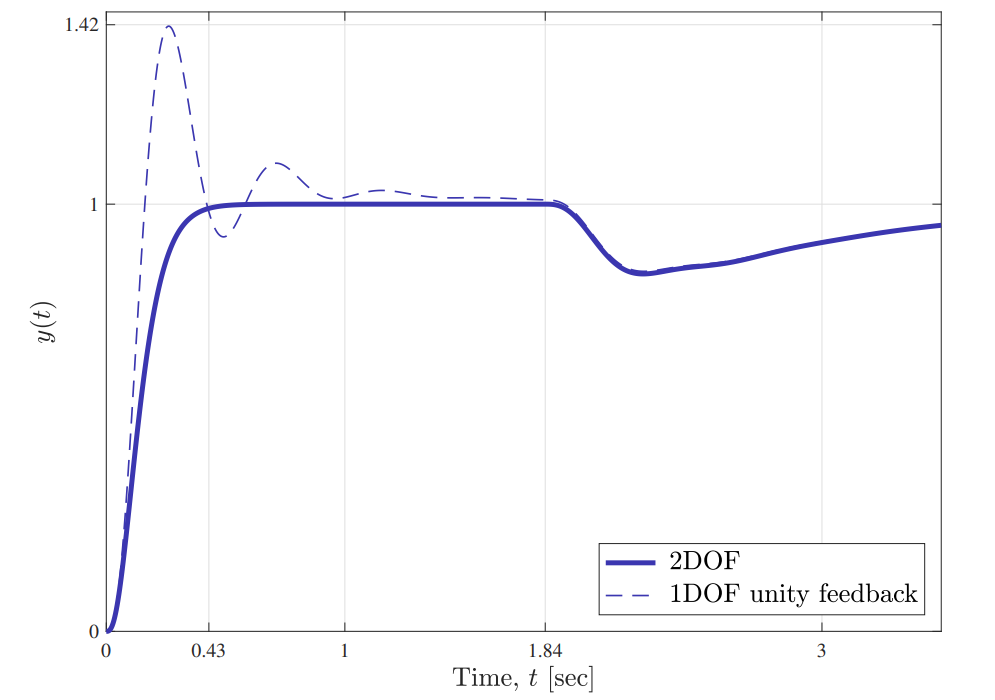
השוואה בתגובת מדרגה בין משוב יחידה בחוג סגור ובין מערכת בשתי דרגות חופש. ב- הוכנסה הפרעה למערכת.