מבוא
מ-(Lynch & Park, 2017):
רובוטיקה הוא תחום די צעיר עם מספר מטרות, כאשר המרכזי ביניהן הוא יצירת מכונות המסוגלות להתנהג ולחשוב כמו בני אדם. הניסיון הזה ליצור מכונות אינטליגנטיות מוביל אותנו באופן טבעי לבחון את עצמנו - לשאול, למשל, מדוע הגוף שלנו מעוצב כפי שהוא, איך הגפיים שלנו מתואמות אחת עם השנייה, ואיך אנו לומדים ומבצעים משימות מורכבות.
בקורס נתמקד על המכניקה, התכנון, והשליטה למנגנונים רובוטים. זרועות רובוטים הם דוגמה מוכרת לאחד. בעיקרון, מנגנון בנוי מחיבור גופים קשיחים, הנקראים חוליות (links), ע”י מפרקים (joints). הנעה/הפעלה (actuation) של המפרקים, לרוב ע”י מנועים חשמליים, גורמת לרובוט לנוע ולהפעיל כוחות בדרכים הרצויות.
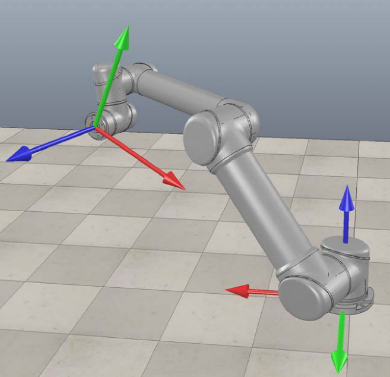
הדגמה של זרוע רובוטית תעשייתית. (Lynch & Park, 2017).
מרחב קונפיגורציה
השאלה הכי בסיסית שאנו יכולים לשאול לגבי הרובוט היא, איפה הוא? התשובה ניתנת ע”י הקונפיגורציה של הרובוט - פירוט המיקומים של כל הנקודות של הרובוט. מאחר והחוליות של הרובוט קשיחים (ובהנחה אנו יודעים את צורתם), מספיק לנו לדעת רק חלק מאוד קטן מהמיקומים של הנקודות - דרגות חופש ברטט.

דרגות חופש של גופים שונים. (Lynch & Park, 2017).
דרגות חופש של רובוט
נביט במקרה הפשוט ב-(a) באיור לעיל, הכולל גוף קשיח יחיד המחובר לקיר ע”י מפרק צירי. למערכת זו רק דרגת חופש אחת, הזווית
מפרקים רובוטיים
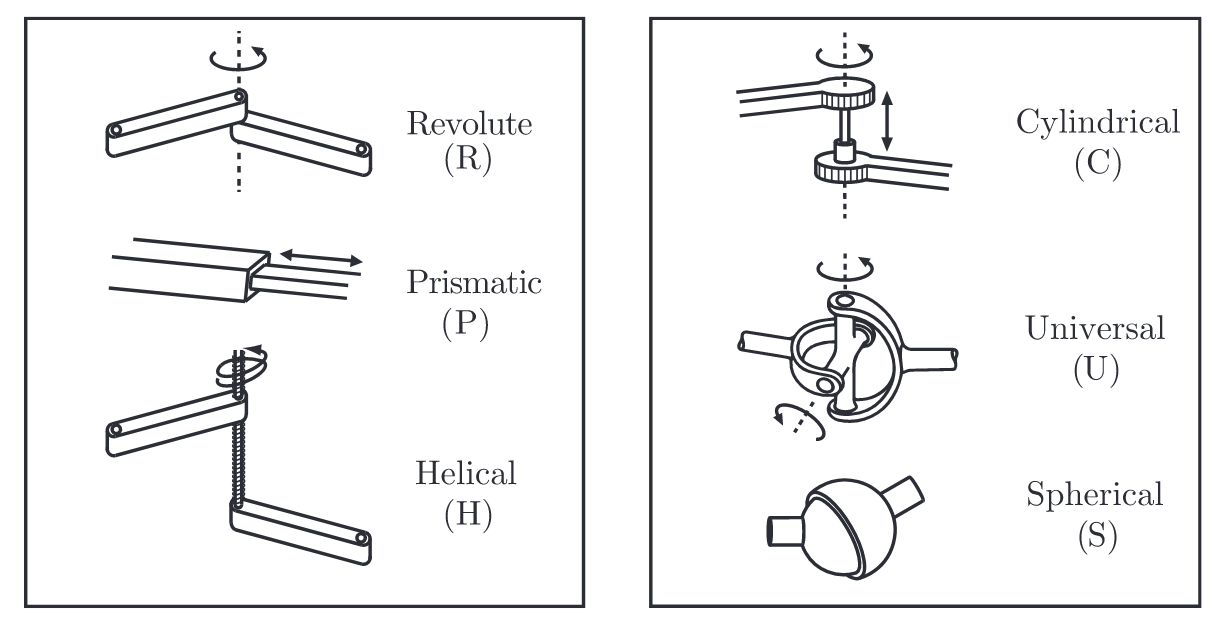
מפרקים רובוטיים טיפוסיים. (Lynch & Park, 2017).
באיור לעיל מתוארים המפרקים הבסיסיים ברובוטים טיפוסיים. כל מפרק מחבר בדיוק שתי חוליות; מפרקים שמחברים שלושה או יותר מפרקים אסורים.
ניתן לחשוב על מפרק כמנגנון שמאפשר לגוף קשיח אחד לנוע ביחס לגוף קשיח אחר. ניתן לחשוב עליו גם כאילוץ על התנועות האפשרויות של שני הגופים הקשיחים שהוא מחבר. האילוצים שכל סוג מפרק מספק נתון בטבלה הבאה:
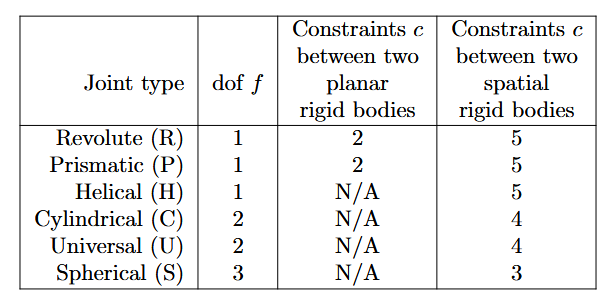
מספר דרגות החופש
ואילוצים המסופקים ע”י מפרקים טיפוסיים. (Lynch & Park, 2017).
נוסחת גרובלר
טוב יש איזה מישהו שקוראים לו גרובלר (Grübler) ויש לו נוסחה:
נוסחה:
נביט במנגנון הכולל
חוליות, כאשר האדמה גם כן נחשבת לחוליה. יהי מספר המפרקים, מספר דרגות החופש של גוף קשיח ( למנגנונים מישוריים ו- למנגנונים מרחביים), הוא מספר דרגות החופש ממפרק , ו- הוא מספר האילוצים ממפרק , כאשר לכל . אז נוסחת גרובלר למספר דרגות החופש של הרובוט היא:
הערה:
נוסחה זו היא סבבה והכל אבל היא לא נכונה תחת תנאים מסוימים, למשל כאשר האילוצים מהמפרקים לא בלתי תלויים אחד בשני.
סיבוב גוף קשיח
טוב צריך טיפה להיזכר בטרנספורמציות סיבוב. נדבר קצת יותר במפורש על מטריצות סיבוב. נרצה גם לנסח במפורש צורת דיבור המאפשרת לנו להבדיל בין נקודות מבט שונות, ולעבור מאחת לשנייה, מה שמאוד יעזור לנו כאשר ננתח כל אחד מהמפרקים של הרובוט.
מערכת ייחוס (reference frame) ניתנת למיקום בכל המרחב, וכל מערכת ייחוס מובילה לייצוג תקין של המערכת והגופים הרלוונטיים בה. תמיד נניח שיש מערכת קבועה (fixed frame), או מערכת מרחב (space frame) שנסמן
את המיקום של הגוף במערכת הקבועה נסמן:
וגם את הצירים של המערכת גוף נוכל לבטא כ:
נוכל להגדיר
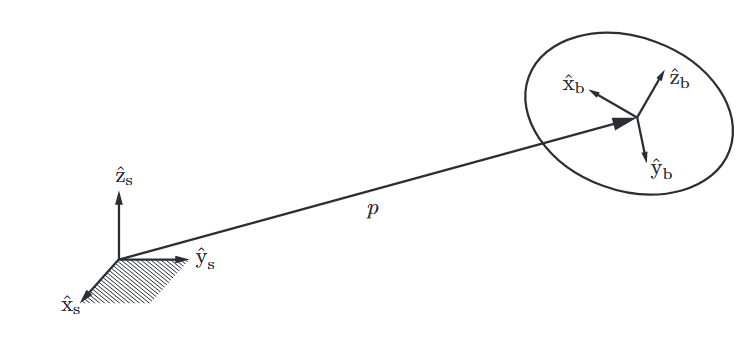
תיאור מתמטי של מיקום ואוריינטציה.
מטריצות סיבוב
כאשר אנו רוצים לתאר סיבוב של גוף קשיח כלשהו ע”י מטריצה, יש לנו תשעה איברים במטריצה שנוכל לעבוד איתם. אבל, מאחר ויש לאוריינטציה של הגוף רק שלושה דרגות חופש, רק שלושה מתוך התשעה יכולים להיבחר באופן בלתי תלוי. נתחיל מלבטא את ששת האילוצים על הערכים של
- כל שלושת הוקטורים
- תנאי האורתוגונליות -
שימושים של מטריצות סיבוב
ישנם שלושה שימושים עיקריים למטריצות סיבוב
- לתאר אוריינטציה.
- לשנות את מערכת הייחוס בו וקטור או מערכת כלשהו מיוצגת.
- לסובב וקטור או מערכת.
כדי לייצג זאת, נביט באיור הבא:
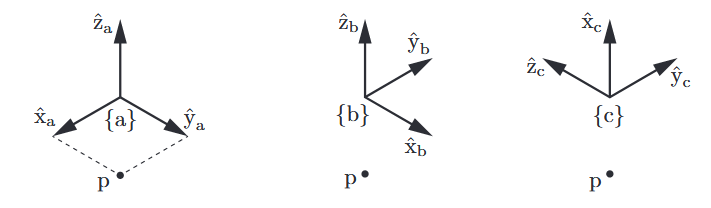
אותה המערכת ואותה הנקודה מיוצגת בשלושה מערכות שונות עם אוריינטציה שונה. המערכת הקבועה,
, מיושרת עם .
האוריינטציה של שלושת מערכות אלו יחסית ל-
והמיקום של נקודה
נשים לב ש-
הערה:
למען האמת, המערכות בקורס לרוב מסומנות במספרים
במקום אותיות . את הסיבוב ממערכת ייחוס למערכת ייחוס אנו מסמנים ב- . את המערכת הקבועה אנו מסמנים ב- .
כאשר אנו רוצים לתאר סיבוב קצת יותר מסובך, למשל סיבוב בזווית מסוימת סביב אחד מהצירים הראשיים, ניזכר כי זה מתבטא בצורה:
נגיד ו-
- כאשר נרצה לסובב מערכת ביחס למערכת קבועה, נכפול משמאל.
- כאשר נרצה לסובב מערכת ביחס למערכת סובבת, נכפול מימין.
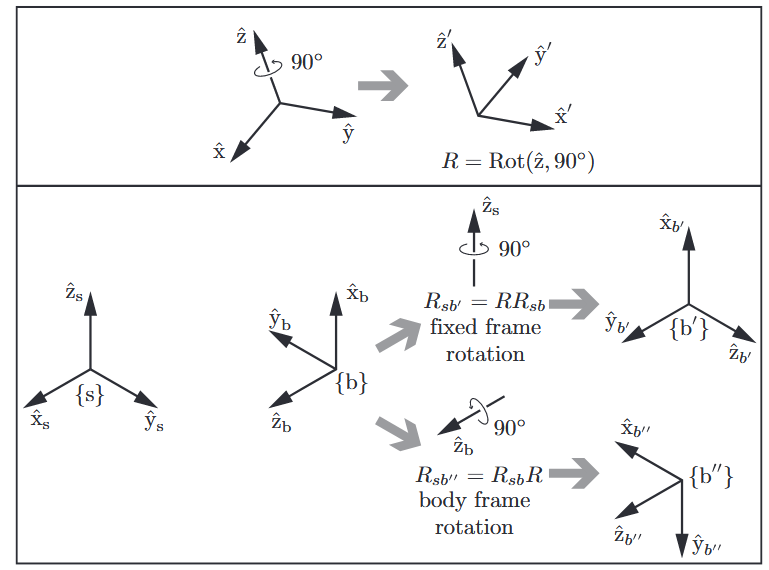
אופרטור הסיבוב
מסובב את המערכת באופן שונה אם הוא מוכפל משמאל או מוכפל מימין. הסימונים בספר קצת שונים, אבל העיקרון אותו עיקרון.
חילוץ ציר סיבוב וזווית סיבוב ממטריצת סיבוב
בהינתן מטריצת סיבוב
זווית הסיבוב
כאשר פעולת ה-
ציר הסיבוב
תנועת גוף קשיח
כאשר אנו רוצים לתאר גם סיבוב וגם טרנסלציה (translation), נוח לנו להשתמש במטריצה
כל טרנספורמציה מהסוג לעיל היא טרנספורמציה מ-הקבוצה האוקלידית המיוחדת
הערות:
- בקורס משתמשים ב-
לסימון מטריצת הטרנספורמציה, במקום . - בהמשך לא נרשום יותר את קווי ההפרדה בתוך המטריצה.
אופן השימוש במטריצות טרנספורמציה אנלוגי לחלוטין לאופן השימוש במטריצות סיבוב. למשל, כאשר אנו רוצים לבצע טרנספורמציה למערכת מסוימת ביחס למערכת קבועה, אנו נכפיל אותה משמאל.
תרגילים
תרגיל 1
נתון הגוף הבא:
איור 1.1: סכמת הגוף.
סעיף א’
נדרש לחשב את מטריצות הטרנספורמציה ההומוגניות הבאות:
פתרון:
כדי לעבור מ-
לכן מטריצת הסיבוב מ-
לכן:
באותו אופן עבור שאר המעברים:
נוכל כעת לבצע אלגברה מגעילה:
נקבל:
וגם:
ונקבל:
סעיף ב’
חשבו את זווית הסיבוב וציר הסיבוב ממערכת
פתרון:
בתרגיל הקודם חישבנו את מטריצת הסיבוב בין שתי מערכות הצירים:
לפי חילוץ ציר סיבוב וזווית סיבוב ממטריצת סיבוב:
ועבור הכיוון:
נשאר רק לתרגם למערכת הקבועה:
