פנגייה

MCS1_007 רזונטורים

• זמן קריאה: 9 דק'

רזונטור לינארי חד-ממדי

נביט במערכת מסה-קפיץ-מרסון הבאה:

איור 7.1: רזונטור לינארי חד-ממדי.

משוואת התנועה של מערכת זו נתונה ע”י:

ניתן לרשום אותה באופן אל-ממדי (ראו רטט):

כאשר:

הערה:

הקשר בין ו- הוא , כאשר הוא יחס הריסון.

הפתרון של (7.2) הוא סכום של הפתרון ההומוגני ופתרון פרטי.

פתרון הומוגני:
נביט במשוואה (7.2) בצורתה ההומוגנית, . נניח פתרון מהצורה . נציב לתוך המשוואה ונקבל:

הפתרונות של משוואה זו הם:

  • אם : יש שני פתרונות ממשיים עבור , ו:

    נשים לב שהארגומנטים בשני האקספוננטים הם שליליים.
    אם אין מהירות התחלתית:

    וגם:

    אם לעומת זאת, אין תזוזה התחלתית, אז , ואז נקבל:

  • אם , אז יש רק פתרון אחד עבור ו-:

  • אם , אז ישנם שני פתרונות מרוכבים עבור , ו-:

    נוכל לסמן , ואז נוכל לרשום זאת כ:

    מאחר וכל קומבינציה לינארית של שני פתרונות אלו יכולים להיות פתרונות למשוואה ההומוגנית הכללית, נוכל לבחור לכפול כל אחת מהם פי ולקחת את הסכום, או לכפול כל אחד מהם פי , ולקחת את ההפרש. במקרה זה, הפתרון יהיה פשוט:

פתרון פרטי:
נניח פתרון מהצורה . כאן, ההוספה של לקבוע לא משפיע על כלליות הפתרון, אבל הוא במכוון נבחר שם כי זה נותן משמעות פיזיקלית לפתרון, כפי שנסביר בהמשך. הקינמטיקה היא לפיכך:

נציב בחזרה ב-(7.2) ונקבל:

נסיק ש- הוא מספר מרוכב:

האמפליטודה של היא:

והפאזה היא:

כך ש:

נוכל להגיע ל-(7.12) גם בלי מספרים מרוכבים. נכתוב את (7.2) כ:

נציע פתרון מהצורה:

נציב ב-(7.15):

נוציא גורם משותף:

לאחר העברת אגפים:

כדי שמשוואה זו תתקיים בכל זמן נתון, הרכיב בכל אחד מהסוגריים המרובעים חייב להיעלם. זאת משום ש- ו- הן פונקציות בלתי תלויות לינארית, ולכן אם סכום כפולותיהן שווה לאפס לכל , אז מקדמיהן חייבים להתאפס.

נסיק מהסוגריים המרובעים ש:

ולכן:

נציב בסוגריים המרובעים השניים ב-(7.19) ונקבל:

נפתור עבור ונקבל את (7.12):

תהודה ברזונטור חד-ממדי

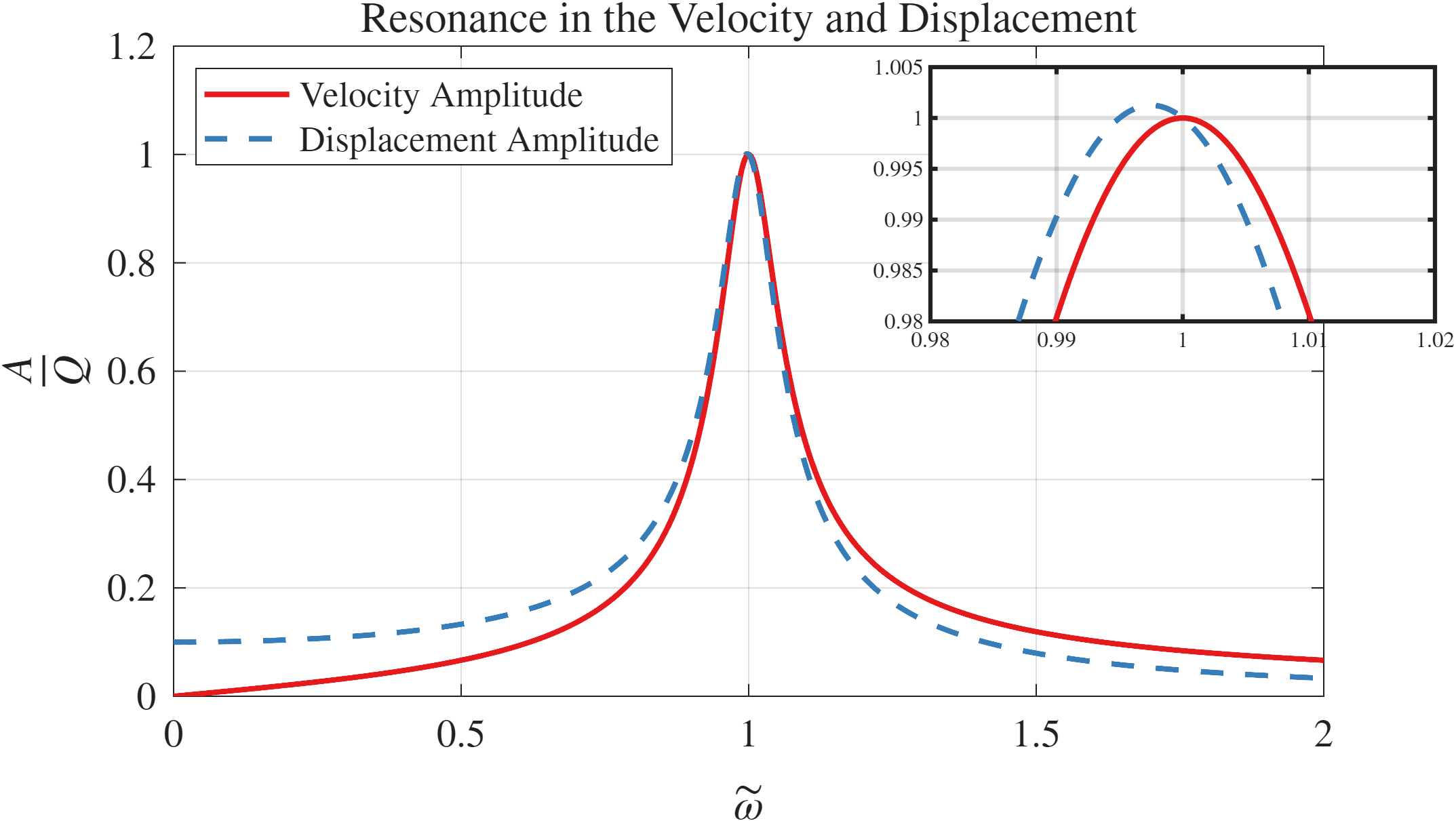
bookhue

איור 7.2: משוואה (7.12) עבור . בנוסף לכך, משורטט האמפליטודה של המהירות, שגודלה הוא כפי שמופיע ב-(7.14b).

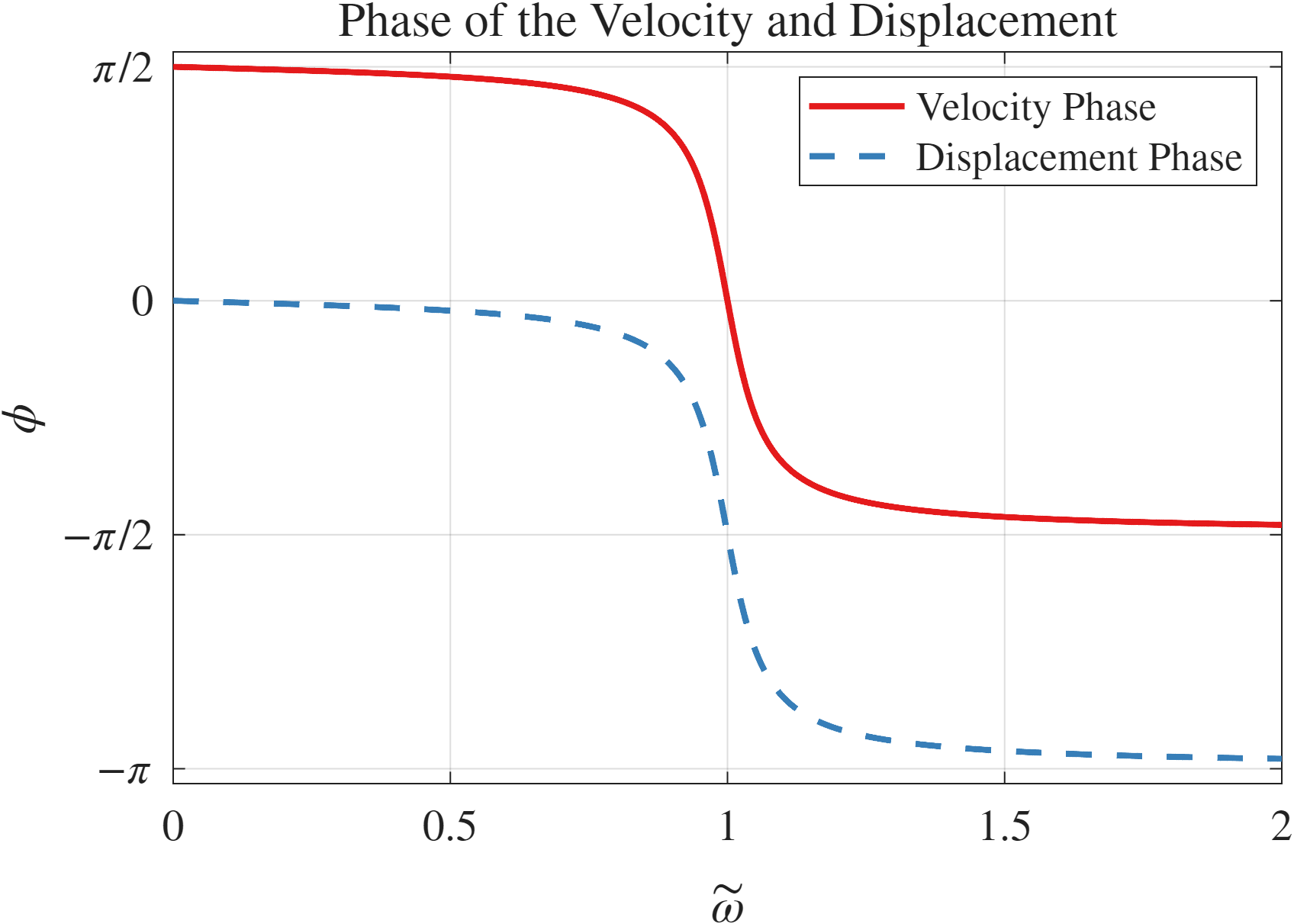
bookhue

איור 7.3: פאזה של המיקום לפי (7.13) עבור . ב-(7.14b) ניתן לראות שהפאזה של המהירות נמצאת ב- מוקדם יותר.

הפאזה כאשר , שואפת ל-. המשמעות של זה היא שהמהירות המקסימלית מקדימה את הכוח המקסימלי ב-.
ניתן לראות שבאזור הפסגות של המיקום והמהירות, הפאזה מתחילה להיעלם. מבט קרוב יותר מראה ש:

  • המהירות מגיעה למקסימום כאשר , וההזזה מגיעה למקסימום בתדירות נמוכה יותר.
  • נדמה כי גם ההזזה המנורמלת וגם המהירות המנורמלת שווים ל-, בתדירות בהם המהירות מגיעה למקסימום.

נבחן כעת את תוצאות אלו ע”י ניתוח אנליטי.

שיא ההזזה מתקבל כאשר :

נשים לב שהמהירות הזוויתית הזאת היא:

  • טיפה יותר קטנה מ- (כלומר, מ-)
  • טיפה יותר גבוה מ-.

שיא ה-מהירות מתקבל כאשר :

ע”י הצבה של (7.24) לתוך (7.13) אנו מוצאים שבתהודה זו:

זה אומר שבתהודה (התהודה במהירות) הפאזה של המהירות יחסית לכוח היא . אם הכוח והמהירות באותה הפאזה, אז ההספק לתוך המערכת במחזור הוא מקסימלי, ולכן התגובה מגיעה לשיא.

ע”י הצבת (7.24) לתוך (7.12) נמצא כי בתהודה (התהודה במהירות) ההזזה והמהירות הם:

אם נחשב את שיא ההזזה ב- , נמצא שהשיא בהזזה הוא:

שיא זה אמנם יותר גדול מ-, אבל עובדה זו לא נושאת איתה הרבה משמעות. מדוע?

  1. עבור מערכות עם גבוה, ההפרש זניח: .
  2. התהודה במהירות () היא בעלת משמעות פיזיקלית ברורה יותר: שם הפאזה בין הכוח למהירות היא אפס, ולכן ההספק המועבר למערכת () מקסימלי.

במונחים של גדלים ממדיים, נקבל:

מה שאומר שגם ההזזה וגם המהירות בתהודה פרופורציונליים לאמפליטודת הכוח ההרמוני, והם פרופורציונליים באופן הפוך למקדם הריסון.
בתהודה, גם הכוח המניע וגם המהירות, הם הרמוניים יחידים, והם בפאזה. אז לאורך כל מחזור, כוח הריסון שווה לכוח המניע:

נציב לתוך (7.2) ונקבל:

במונים ממדיים:

כלומר, נשארנו עם מערכת פשוטה של מסה-קפיץ בעירור חופשי, שבאופן טבעי רוטטת ב- .

חדות התהודה

נביט כעת ברוחב פס, בו האנרגיה במערכת היא חצי מהשיא הערך שלה בתהודה. בתהודה, האנרגיה הקינטית המנורמלת היא פרופורציונלית לריבוע אמפליטודת המהירות: . גבולות התדירות הזוויתית הם כאשר האנרגיה הקינטית יורדת לחצי מערך השיא, כלומר :

פתרון:

לכן, רוחב-הפס של התדירות הזוויתית היא:

את חדות התהודה אנו מגדירים:

הערה:

הערכים ו- הם לא אותו הדבר (אין להם את אותה המשמעות)! יצא לנו מקרה פרטי של רזונטור לינארי חד-ממדי.

מהצבה של (7.38) לתוך (7.13) נקבל את הפאזות:

כלומר, רוחב-הפס הוא בין ו- .

מקדם איכות

בחלק מהספרות, מגדירים את מקדם האיכות כיחס בין האנרגיה השמורה והאנרגיה המתפזרת במערכת - בתדר התהודה:

במקרה של רזונטור לינארי חד-ממדי, האנרגיה המקסימלית במחזור אחד היא או , או . האנרגיה המתפזרת במחזור היא:

נסיק ש:

אבל ההגדרה הזאת של לא תמיד תואמת ל-. בואו נביט כעת במערכת המתוארת באיור הבא:

איור 7.4: רזונטור לינארי חד-ממדי סימטרי, עם pre-stress.

מערכת זו שקולה בכל הפרמטרים שלה למערכת באיור 7.1. אבל, למערכת באיור 7.2 ניתן לבצע pre-stress ע”י הזזה של העוגנים הרחק אחד מן השני. פעולה זו לא תשפיע על הקשיחות, מסה, או ריסון, אבל כן ישפיע על האנרגיה המקסימלית האגורה במערכת.

ניתן להראות שאם המערכת לא לינארית, או אפילו מסדר שני, אז השקילות הזאת בין ל- ובין החדות ל-, נשברת לחלוטין.

רזונטור אלקטרוסטטי מקבילי

נביט כעת במערכת אלקטרוסטטית ונבחן את התגובה הדינמית שלה:

איור 7.5: רזונטור אלקטרוסטטי מקבילי.

כבר בחנו את ההתנהגות של מערכת זו בשיווי משקל במשוואה (1.18) וראינו כי:

איור 7.6: עקומת equilibrium curve של המערכת.

בהזנחת שדות שוליים, משוואת התנועה של מערכת זו היא:

ניתן לרשום את משוואת תנועה זו במונחים אל-ממדיים:

כאשר:

בעבר בחנו לעומק את התגובה הסטטית של המשפעל האלקטרוסטטי. עבור ו- ההזזה האל-ממדית הסטטית היא (ראו משוואה (1.16)):

המצב הסטטי יציב בטווח אם המתח DC מוגבל ע”י . בהנחה ו- נמוך מספיק כדי שהתגובה הדינמית היא רטט נמוך סביב נקודת שיווי המשקל, נוכל לבטא את ההזזה כסכום של הזזה הסטטית ורכיבים דינמיים:

נציב לתוך (7.45), עם פיתוח טיילור לשני משתנים ו-, ולאחר הזנחת איברים ממעלה שנייה ומעלה, נוכל לרשום את משוואות התנועה באופן הלינארי:

התדירות הטבעית המנורמלת האלקטרומכנית היא:

כך שהיא מוגבלת ב-.

התגובה במצב מתמיד של המשפעל נתונה ע”י:

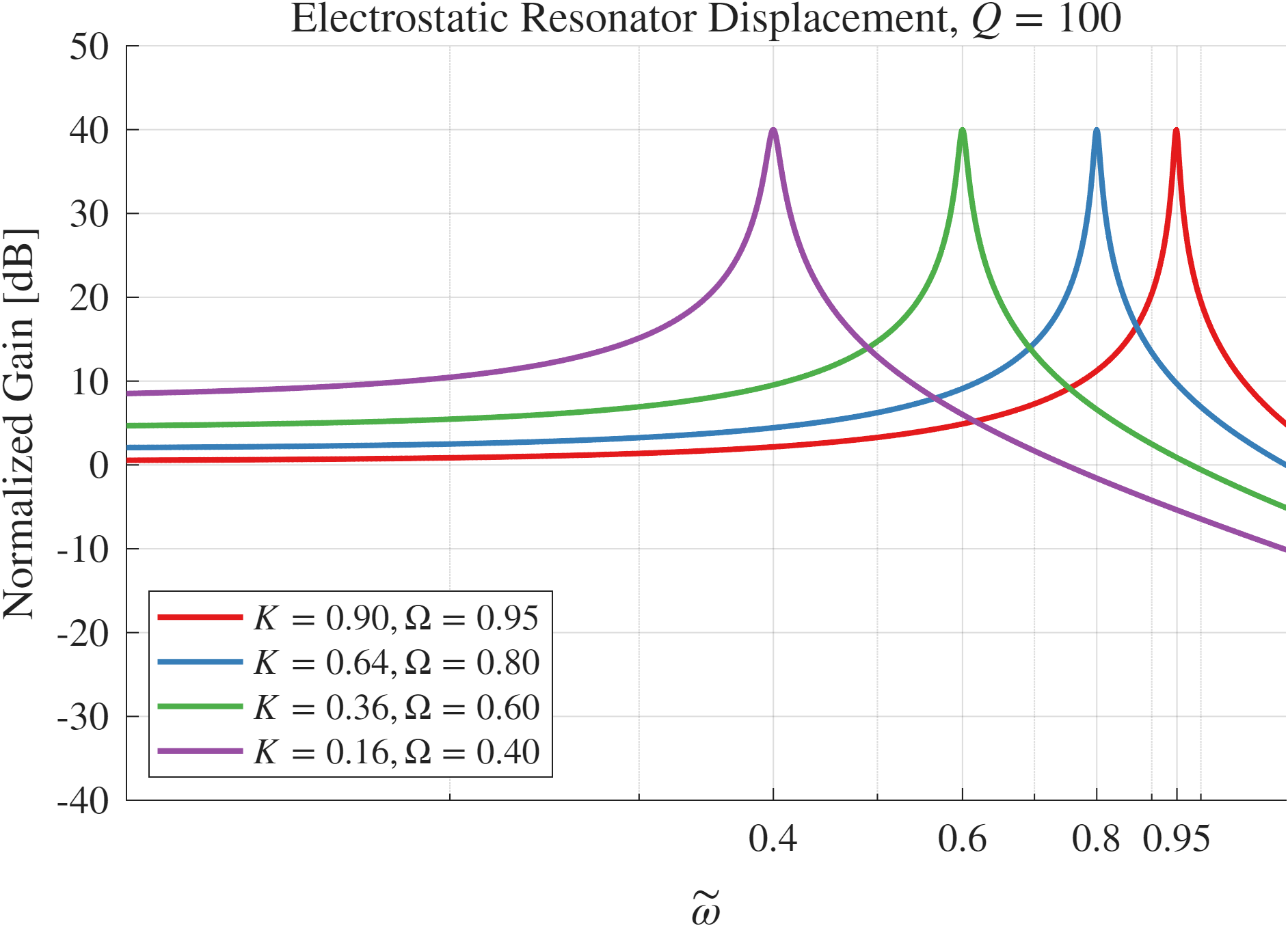
bookhue

איור 7.7: אמפליטודת ההזזה במצב מתמיד של רזונטור אלקטרומכני עם ועומסי DC שונים . ההגברה המנורמלת היא .

הערה:

שיא ההגברה הוא כי ההגברה המנורמלת מגיעה לשיא של בתהודה. בתהודה (), ההגברה היא:

בדציבלים: . כפל ב- בנורמליזציה משווה את כל השיאים ל-, ללא תלות ב-.

Feedthrough

מה אם נוסיף מד-מתח על הפלטה התחתונה?

רזונטור אלקטרוסטטי מקבילי עם מד-מתח.

מגזירה של האנרגיה במערכת, הכוח האלקטרוסטטי הוא:

לרוב, מניעים את המערכת עם , כך שנישאר רק עם:

לכן, כתוצאה מהכוח הממוצע, , התהודה מתרחשת ב:

אם הרכיב המחזורי של הכוח הוא

נסיק כי התהודה מתרחשת ב- , בה התנועה תהיה:

הקיבול יהיה גם מהצורה הזאת:

לפי , המטען על האלקטרודה יהיה:

לכן הזרם יהיה:

כאשר הכוונה לרכיבים מסדר גבוה (high order terms).

לרכיבים ב-(7.60) יש שמות!

  • הרכיב נקרא זרם תנועתי (motional current).
  • הרכיב נקרא feedthrough, ולרוב נרצה להיפטר ממנו.

הזרם התנועתי נובע מהתנועה המכנית של הרזונטור: כאשר המסה תונדת, המרווח משתנה, הקיבול משתנה (), ונוצר זרם. זרם זה נושא מידע על התכונות המכניות של המערכת - תדר התהודה, מקדם האיכות, וכו’. לכן, זהו האות שאנו רוצים למדוד.

ה-feedthrough הוא זרם פרזיטי הזורם דרך הקיבול הסטטי () בעקבות המתח ה-AC המופעל. זרם זה קיים גם ללא תנועה מכנית כלשהי, והוא מסווה את הזרם התנועתי - במיוחד הרחק מהתהודה. בתהודה עצמה, הזרם התנועתי שולט, אבל בתדרים אחרים ה-feedthrough יכול להיות בסדר גודל דומה או אף גדול יותר.

למעשה, נוכל להבחין בתופעת ה-אנטי-תהודה (anti-resonance) באיור 7.7 הנובעת מביטול חלקי בין הזרם התנועתי (בפאזה הפוכה) לבין ה-feedthrough.
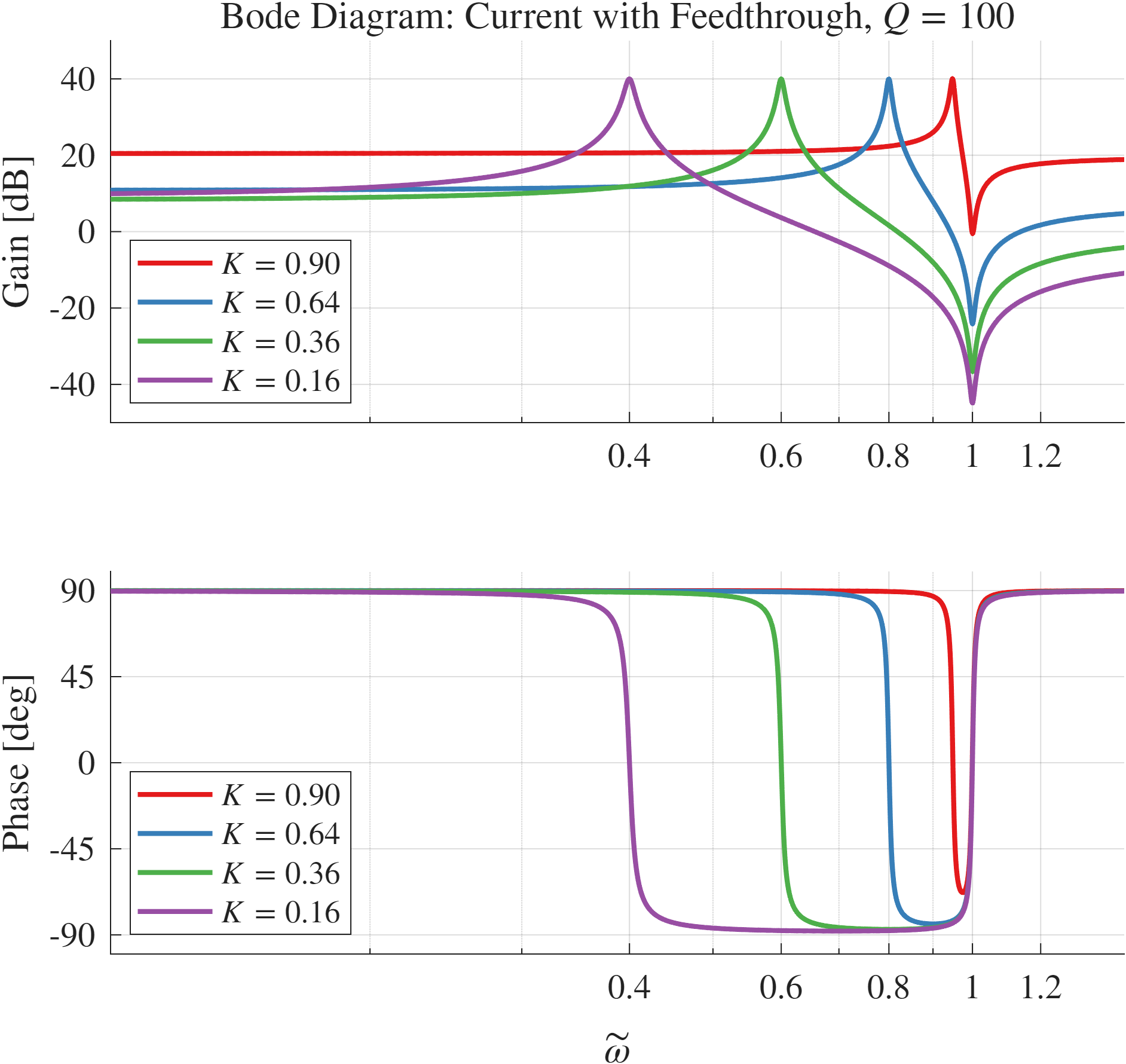
bookhue

דיאגרמת בודה של מגבר ופאזה של הזרם הכולל עבור רזונטור א-סימטרי, . תדר התהודה יורד עם , בעוד תדר האנטי-תהודה קבוע ב-.

עמודים המציינים את העמוד הזה