MCS1_001 מבוא

→ קודם: MCS1_000הבא: MCS1_002 ←

מבוא

היסטוריה של MEMS

סיליקון חד-גבישי (single-crystal silicon) אינו רק חומר אלקטרוני מצוין, אלא הוא גם מפגין תכונות מכניות מעולות. תכונות אלו הביאו להולדתו של תחום המערכות המיקרו-אלקטרו-מכניות (MEMS - Microelectromechanical Systems) בעקבות תעשיית המעגלים המשולבים (IC). במקור, MEMS כללו בעיקר התקנים מכניים המבוססים על סיליקון חד-גבישי, כאשר לפחות אחד או יותר מממדיהם היה בטווח המיקרומטרים.

פיתוח MEMS מכניים מסיליקון חד-גבישי כרוך בייצור חלקים מיקרו-מכניים, כגון ממברנה דקה במקרה של חיישן לחץ או קורה שלוחה (cantilever beam) עבור מד תאוצה. חלקים מיקרו-מכניים אלו מיוצרים על ידי selective etching של אזורים במצע סיליקון כדי להשאיר מאחור את הגיאומטריות הרצויות. המונחים MEMS ומיקרומכניקה נכנסו לשימוש ב-1982 לתיאור תהליכי ייצור אלו. בערך באותו זמן הופיעו גם התייחסויות לטכניקות כמו “bulk micromachining”. הרצאתו של ריצ’רד פיינמן ב-26 בדצמבר 1959 בשם “There’s Plenty of Room at the Bottom” נחשבת על ידי רבים כנקודת הפתיחה של MEMS, אך במובן המעשי, ההמצאה של הטרנזיסטור והתהליכים שפותחו לייצור טרנזיסטורים, שש שנים קודם לכן, היא שאפשרה את MEMS.

איור 1.1: מיניאטוריזיצה (פורסם 1961) כלל את הרצאתו של פיינמן כפרקון האחרון.

איור 1.2: ריצ’רד פיינמן מנגן על תופי בונגו 🙃.

הדחף הראשון לשימוש בסיליקון חד-גבישי כאלמנט מיקרו-מכני ב-MEMS ניתן לייחס לגילוי ה-piezo resistance הגדול שלו. Piezo resistance הוא השינוי בהתנגדות החשמלית של חומרים מסוימים כתוצאה ממאמץ מכני המופעל עליהם. צ’רלס סמית’ מ-Case Institute of Technology, במהלך שבתון ב-Bell Labs ב-1953, חקר את ה-piezo resistivity של מוליכים למחצה ופרסם ב-1954 את המאמר הראשון על האפקט הפיזואלקטרי ב- ו-. מקדמי ה-piezo resistance שסמית’ מדד הוכיחו שה-gauge factor של מדי מאמץ (strain gauges) מסיליקון וגרמניום היה גדול פי עד ממדי מאמץ מסרט מתכתי, ולכן מדי המאמץ ממוליכים למחצה היו צפויים להיות הרבה יותר רגישים.

בעקבות תוצאות אלו, חברות כמו Kulite ו-Honeywell החלו לפתח באופן מסחרי מדי מאמץ מסיליקון החל מ-1958. Pfann ועמיתיו, ב-1961, הציעו טכניקת דיפוזיה של מזהמים (dopant diffusion) לייצור חיישנים פיזואלקטריים מסיליקון למדידת מתח, מאמץ ולחץ. בהתבסס על רעיון זה, Kulite שילבה מדי מאמץ מסיליקון על מצע סיליקון דק עם נגדים מפוזרים ב-1961. כבר ב-1962, Tufte ועמיתיו ב-Honeywell, תוך שימוש בשילוב של selective etching רטובה, selective etching יבשה (באמצעות פלזמה במקום תמיסה) וחמצון, יצרו את הדיאפרגמות הפיזואלקטריות הדקות הראשונות מסיליקון עבור חיישני לחץ. selective etching של סיליקון פותחה קודם לכן לייצור טרנזיסטורים.

איור 1.3: אלמנט מד המאמץ מסיליקון חד-גבישי נראה כפס אנכי ממורכז בין שני רפידות ההלחמה. מד המאמץ מסיליקון חד-גבישי מציע רגישות גבוהה פי 20-50 ממדי מאמץ מנייר מתכתי. (BF Goodrich Advanced Micro Machines.)

לאורך השנים, יישומי MEMS הרבים הובילו לשפע של ראשי תיבות MEMS, חלקם אולי נוצרו על ידי פרופסורים עוזרים המנסים לקבל קביעות מהר יותר.

• BioMEMS = MEMS המיושם בתחום הרפואה והביוטכנולוגיה
• Optical MEMS = עצמים מכניים + מקורות/גלאים אופטיים
• Power-MEMS
• C-MEMS (carbon MEMS עבור המחבר אך ceramic MEMS עבור אחרים)
• HI-MEMS = hybrid insect-microelectromechanical systems
• RF-MEMS = radiofrequency MEMS
• Cif-MEMS = CMOS IC Foundry MEMS
• COTS MEMS = commercial off-the-shelf MEMS
• MOEMS = microoptical electromechanical systems
• P-MEMS = polymer MEMS
• CEMS = cellular engineering microsystems
• HARMEMS = high-aspect-ratio MEMS

חזרה על מכניקה ואלקטרוסטטיקה

עבודה ואנרגיה

בדינמיקה למדנו על עבודה והגדרנו אותה כ:

ועבודה זו נמדדת ביחידות של .
עבור מסה הנגררת במהירות קבועה על קרקע מחוספסת עם מקדם חיכוך , ומפעילים עליה כוח , העבודה שהכוח מבצע על המסה הוא , והעבודה שמתבצעת ע”י החיכוך היא .

ראינו כי עבור כוחות משמרים ניתן להגדיר פונקציית פוטנציאל:

כאשר הוא אופרטור הגרדיאנט, ו- היא פונקציית הפוטנציאל (הסקלרית).

במקרה של אלקטרוסטטיקה, אנו דנים במטענים שפועלים ביניהם כוחות מרכזי, שלמדנו שניתן להוכיח שהם כוחות משמרים. כוחות מרכזיים אלו ניתנים ע”י חוק קולון:

כאשר היחידות של משוואה זו הם:

את הסיבה לקשר , ואת היחידות של נמצא ונחשב בהמשך.

איך מדדו את מטענו של האלקטרון?

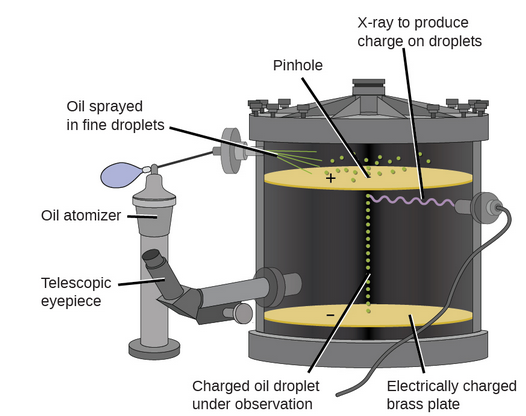
מטענו של האלקטרון נמדד לראשונה בניסוי מיליקן, הנקרא גם ניסוי טיפת השמן, הנערך ע”י רוברט מיליקן בשנת 1909.

מיליקן יצר טיפות שמן מיקרוסקופיות שניתן היה לטעון חשמלית באמצעות חיכוך במהלך היווצרותן או באמצעות קרני רנטגן. טיפות אלו נפלו בתחילה בשל כוח הכבידה, אך ניתן היה להאט או אפילו להפוך את תנועתן באמצעות שדה חשמלי. על ידי כיוון עוצמת השדה החשמלי וביצוע מדידות וחישובים מדויקים, מיליקן הצליח לקבוע את המטען על טיפות בודדות.

איור 1.4: ניסוי מיליקן מדד את המטען של טיפות שמן בודדות. (CC BY 4.0; OpenStax)

במבט על נתוני המטען שמיליקן אסף, ניתן לזהות כי המטען של טיפת שמן הוא תמיד כפולה של מטען ספציפי, . מיליקן הסיק שערך זה הוא מטען יסודי - המטען של אלקטרון בודד - כאשר המטענים שנמדדו נבעו מעודף של אלקטרון אחד (), שני אלקטרונים (), שלושה אלקטרונים (), וכן הלאה, על טיפת שמן נתונה.

נוכל להגדיר שדה כוחות עבור מטען בודד בצורה:

כאשר היחידות של משוואה זו הם:

כמו במכניקה, גם באלקטרוסטטיקה אנו מגדירים פונקציית פוטנציאל. למשל, עבור מטען יחידה שבאופן קוואזיסטטי נדחף ע”י כוח מאינסוף למרחק ממטען מקור , העבודה על החלקיק היא:

כאשר לגודל זה המידות הן .

העבודה שמתבצעת ע”י הכוח היא חיובית והיא מושקעת אל תוף האנרגיה הפוטנציאלית של מטען היחידה. לכן האנרגיה הפוטנציאלית היא:

כך ש:

נשים לב שהיחידות הן:

אנו יודעים שכאשר אנו מכפילים כוח בהזזה, נקבל אנרגיה . מה עם פוטנציאל חשמלי? במה נכפיל פוטנציאל אלקטרוסטטי כדי לקבל אנרגיה ביחידות של ? כמובן שנכפילו בקולון !
מבחינה פילוסופית, ניתן לחשוב על מתח ומטען כצמודים במרחב האלקטרוסטטי, כמו שכוח ותזוזה הם צמודים בעולם המכני.

כעת נוכל לפתח את המידות של :

לרוב נמדד ב-Farad () למטר - , אבל זוהי מידה שימושית יותר לעולם האלקטרוניקה, פחות ל-MEMS. כתוצאה מניסויים נמצא שגודלו הוא:

כעת, נגדיר את השטף האלקטרוסטטי שהוא הצמוד לשדה החשמלי:

שטף חשמלי? לא הגדרנו את זה אחרת ב פיזיקה 2?

כן, יש מלא חוסר החלטיות במונחים בין התחומים השונים - אלקטרוסטטיקה, מכניקה, זרימה, מגנטיות וכו’. We are human after all. כאן כשאנו אומרים שטף, למעשה אנו מתכוונים לצפיפות שטף חשמלי, אז אולי כדאי שמעכשיו נקרא לזה צפיפות שטף חשמלי.

לצפיפות השטף יש את היחידות והוא פונקציה לינארית של השדה. אם נבצע אינטגרציה של המכפלה של השדה וצפיפות השטף, בכל נקודה במרחב, כאשר השדה גדל מ- לגודל סופי , נקבל:

כלומר:

שזהו גודל סקלרי והיחידות שלו הם , והוא מתאר את האנרגיה ליחידת נפח. למידה זו יש את אותן היחידות כמו מאמץ מכני. במובן מסוים גודל זה מקביל לאנרגיה ליחידת נפח של שדה מאמצים

נקבל:

בחזרה לאלקטרוסטטיקה, צפיפות השטף החשמלי סביב מטען היא לפיכך:

צפיפות השטף החשמלי נקראת לפעמים תזוזה חשמלית.

בהינתן קבל לוחות מקביל עם ריק בין הפלטות, האם קיים מאמץ בריק?

מצד אחד, מאמץ לא יכול להתקיים בריק - אין מה שיחווה עיבור, אין מאמץ. אבל, מצד שני, יש שדה חשמלי בין הלוחות, ולפיכך יש אנרגיה ליחידת נפח בין הלוחות . נוכל לומר כי יש מאמץ חשמלי/אלקטרוסטטי בין הלוחות - הריק מחזיק את המאמץ החשמלי הזה.
ההבדל הוא הבדל עקרוני - עלינו להבין שאנו כעת לומדים נושא העוסק הן במכניקה והן באלקטרוסטטיקה. אנו חייבים ללמוד להיאבק בשני תחומים אלו בו זמנית.

חוק גאוס

חוק גאוס עבור שטף אלקטרומגנטי קבוע כי:

כאשר הוא הנורמל למשטח סגור ו- הוא צפיפות המטען (מטען ליחידת נפח) בנפח . חוק גאוס קובע כי כמות השטף העוזבת משטח סגור שווה לכמות המטען התחום במשטח סגור זה. לפי משפט הדיברגנץ:

נציב בחוק גאוס:

אם אחיד, נסיק כי:

שזוהי אחת מהצורות של חוק גאוס הדיפרנציאלי. משוואה (1.5) היא למעשה משוואת פואסון, ואם אז היא פשוט משוואת לפלס:

קבל אלקטרוסטטי

נביט בקבל לוחות אינסופיים מקביל עם מטענים הפוכים:

איור 1.5: גודל שדה חשמלי בשלושה אזורים שונים בקבל מקביל.

המרחק בין הלוחות הוא . ללוח השמאלי יש צפיפות מטען שטחית אחידה , ולימנית יש צפיפות מטען שטחית אחידה . ניתן לחשב שהשדה בין הפלטות הוא והמתח הוא .

אם נביט בשטח של קבל זה, הוא נושא מטען . לפיכך:

לכן נהוג להגדיר את הקיבול של הקבל כ:

כאשר המידות של הגדרה זו הם:

האנרגיה האלקטרוסטטית של הקבל היא:

נשים לב שבאזור בין הקבלים גודל השדה החשמלי הוא . באזורים מחוץ לקבלים הוא !
כמו במכניקה נוכל להגדיר כוח וקטור הטרחה , שנזכור שהוא תמיד מוגדר החוצה מהמשטח עליו הוא מוגדר. על כל פלטה, וקטור ההטרחה תלוי אך ורק במטען של הפלטה המקבילה - כי מטען חשמלי לא מפעיל שדה חשמלי על עצמו, רק החוצה (לכן יש בביטוי להלן):

נרצה כעת להגדיר קבל אידיאלי. בהזנחת קצוות הקבל (נהוג עבור קבל ארוך ודק) ונוכל לומר:

עבור קבל אלקטרוסטטי אנו יכולים לחשב את ה-מצב האלקטרוסטטי ע”י פתרון משוואת לפלס:

עם התנאי שפה המתאימים.

ברגע שאנו יודעים לחשב את התפלגות המתח, נוכל לחשב את השדה החשמלי מהגרדיאנט:

לאחר מכן אנו מחשבים את ההטרחה:

כעת נוכל לבצע אינטגרציה לאורך ההטרחה בשפה כדי לקבל את הכוח האלקטרוסטטי השקול.

משפעל מקביל

הפעלת מטען

המערכת הבאה כוללת קבל לוחות מקביל, כאשר הפלטה התחתונה מוארקת והפלטה העליונה היא מוחזקת ע”י קפיץ לינארי בעל קבוע . כאשר הקפיץ לא מתוח המרחק בין הפלטות הוא (עבור gap).

על המערכת אנו מפעילים מטען (על הפלטה העליונה).

איור 1.6: מערכת משפעל פלטה מקבילה מופעלת מטען.

הקיבול של המערכת היא:

כאשר הוא דרגת חופש שאנו רוצים לשלוט בה.
סך הפוטנציאל של המערכת הוא:

נציב (1.8) ונקבל:

נרצה כעת לחשב את הכוח הריאקטיבי - הכוח הדרוש כדי להביא את דרגת החופש למצב כלשהו. הכוח הריאקטיבי הוא הנגזרת הראשונה של סך האנרגיה הפוטנציאלית של המערכת, ביחס לדרגת חופש במערכת (במקרה שלנו ):

מה זה? מאיפה זה נובע?

מדובר בכוחות מוכללים. כעיקרון, ראינו שהעבודה המתבצעת ע”י כוח בתזוזה קטנה היא:

האנרגיה הפוטנציאלית מוגדרת כמינוס העבודה ע”י כוחות משמרים:

כלומר:

את אנו מגדירים הפוך - הכוח שהקפיץ או השדה החשמלי מפעילים כדי להביא את המערכת ל- מסוים:

נקבל:

נקבל שיווי משקל כאשר:

נוכל לשרטט עקומה עבור קשר זה בין המשתנה שאנו מפעילים () ל-, הנקראת equilibrium curve של המערכת:

איור 1.7: עקומת equilibrium curve של המערכת.

כלומר, עבור כמויות שונות , בין אם הוא חיובי או שלילי (הוא מועלה בריבוע), נקבל נקודת שיווי משקל המשתנה לינארית חיובית.

הקשיחות של המערכת היא הנגזרת הראשונה של כוח הריאקטיבי ביחס לדרגת החופש שלנו:

במקרה שלנו זה פשוט:

הפעלת מתח

נביט באותה המערכת, רק שהפעם אנו מפעילים מתח על הפלטה העליונה, ולא מטען . כלומר, המטען על הפלטה העליונה עלול להשתנות, והוא ישתנה בהתאם לתנאי המערכת.

אנרגיית הפוטנציאל של מקור המתח היא:

כאשר הוא המטען ש-נלקח מהסוללה.

סך הפוטנציאל במערכת הוא (לא לשכוח את אנרגיית מקור המתח!):

האנרגיה הפוטנציאלית של הסוללה היא:

כאשר הוא המתח של הסוללה, הוא המטען ההתחלתי על הסוללה ו- הוא המטען שיצא מהסוללה ועבר לפלטה (אלקטרודה) העליונה.

כפי שהראנו ב-(1.8), הקיבול תלוי בתזוזה :

אבל מנקודת המבט האלקטרוסטטית, היא לינארית מהמובן ש:

נסיק שסך האנרגיה הפוטנציאלית ניתנת לכתיבה באופן:

נקבל:

לכן כוח הריאקטיבי יהיה:

נשים לב שהביטוי לא מושפע מ-, ולכן לרוב נתעלם ממנו.

נמצא שיווי משקל:

הקשיחות של המערכת:

נוכל כעת למצוא את הקשיחות של המערכת בשיווי משקל:

ה- equilibrium curve של המערכת היא לפיכך:

איור 1.8: עקומת equilibrium curve של המערכת.

המערכת היא יציבה אם , לא-יציבה אם , ו-אדישה אם .
אבל, אם , ו-ללא שינוי העומס בקרבה לשיווי משקל, אז המערכת היא יציבה קריטית. הפרמטרים לנקודת ה-pull-in הם:

אם נציב את זה חזרה בתנאי ש”מ נקבל:

תצורה על ממדית

להכללת הבעיה הבעיה אנו נרצה לרוב להגיע לתצורה על ממדית של הביטויים שקיבלנו, לפי המחשבה ש-”פתרנו אחד, פתרנו את הכל”. אבל, עלינו לזכור שהרבה פעמים נצטרך לפתור גם את התצורה הממדית של הבעיה - הרי בסופו של יום מישהו צריך לבוא ולייצר את התכן שלנו.

נביט בפוטנציאל שחישבנו עבור פלטות מקבילות בהפעלת מטען:

ננרמל את עם :

נגדיר ונקבל:

נוכל גם לנרמל לפי :

נוכל לחשב את הכוח הריאקטיבי:

לכן התנאי לש”מ הוא:

הקשיחות היא פשוט:

עבור הפעלת מתח:

נגדיר:

נקבל:

נוכל להגדיר:

ולכן:

לכן הכוח הריאקטיבי:

נקבל ש”מ כאשר:

הקשיחות היא:

בש”מ:

מדוע שפעול אלקטרוסטטי יעיל אך ורק בקנה מידה מקרוסקופי?

במוט באורך עם שטח חתך ומודול יאנג הקשיחות שלו היא:

נביט שוב ב-(1.27) (נחזור טיפה אחורה בנרמול):

אם היינו משתמשים במוט במקום הקפיץ הלינארי, היינו מקבלים:

נשים לב שאם נקטין את כל הממדים (אורך, ולפיכך גם שטח) פי , הכוח המכני הריאקטיבי בצד שמאל של המשוואה קטן פי , בעוד הכוח האלקטרוסטטי בצד ימין לא משתנה כלל (כל עוד לא משתנה).

מדוע שפעול אלקטרוסטטי יעיל יותר משפעול אלקטרומגנטי?

כאשר מפעילים כוח אלקטרוסטטי על גוף נייח, לא נדרשת עבודה. לעומת זאת, בשפעול אלקטרומגנטי, כוח קבוע מופק על ידי זרם קבוע העובר דרך סליל, מה שדורש הספק כניסה - כלומר נדרשת עבודה.

מדוע השפעת כוח הכבידה יורדת עם קנה המידה?

נביט בכיפוף של קורה שלוחה עקב משקלה העצמי. כפישוט, נוכל להפעיל את כל משקל הקורה ככוח מרוכז, המופעל בקצה הרחוק של הקורה. במקרה זה, התזוזה של הקצה הרחוק תהיה:

שוב, הגיוני יותר לשקול את תזוזת הקצה ביחס לאורך:

כאשר מקטינים את כל הממדים פי , הצד הימני יורד פי . מכאן נובע שהשפעת כוח הכבידה (למשל, התכופפות עקב משקל) יורדת לינארית עם הגודל.

מדוע החוזק עולה עם הקטנת קנה המידה?

קנה מידה לא משפיע על עיבור או מאמץ. אבל, בחומרים שבירים, החוזק עולה ככל שהממדים יורדים (נשווה את החוזק של זכוכית המשמשת בחלונות לעומת החוזק של סיבי זכוכית). הסיבה לכך היא שסטטיסטית יש פחות אתרי גרעינים לסדקים.

תרגילים

נזכור שכאשר אנו מפעילים מתח:

וכאשר מפעילים מטען:

תרגיל 1

במערכת משפעל זוויתי אלקטרודה תחתונה מקובעת והאלקטרודה העליונה מחוברת לקפיץ פיתול בעל קשיחות המקנה אפשרות לתנועה זוויתית בלבד. הוא אורך האלקטרודה, ו- העומק. המרחק ההתחלתי בין האלקטרודות הינו כאשר .

איור 1.9: מערכת משפעל זוויתי.

במה שונה הפעלת מטען מהפעלת מתח?

הפעלת מטען

ראשית, ננסח את האנרגיה הפוטנציאלית של המערכת:

חישוב הקיבול כתלות בזווית תחת הנחת זוויות קטנות:

נניח זוויות קטנות :

נרצה לנרמל את הקיבול כדי לפשט את הביטוי. ראשית ננרמל את הזווית לפי הביטוי בסוגריים, :

נוכל להמשיך לנרמל את הקיבול:

נציב לביטוי של האנרגיה:

נראה כאילו רק סיבכנו. trust the process.
נחלק ב- :

נוודא רגע שבאמת הביטוי הוא חסר יחידות:

קיבלנו את הביטויים לגדלים המנורמלים:

כעת הביטוי הסופי לאנרגיה:

נחשב את הכוח הריאקטיבי (שהוא מומנט) ע”י גזירה לפי דרגת החופש המנורמלת :

נמצא את התנאי לשיווי משקל. שיווי משקל מתקבל כאשר הכוח הריאקטיבי מתאפס:

נחשב את את הקשיחות ע”י גזירת הכוח ההגבי לפי דרגת החופש :

נחשב כעת את הקשיחות במצב שיווי משקל (ע”י הצבת התנאי שקיבלנו לתוך הביטוי לקשיחות):

עבור סך יציבות נבדוק מתי הקשיחות במצב ש”מ מתאפסת:

באופן גרפי:

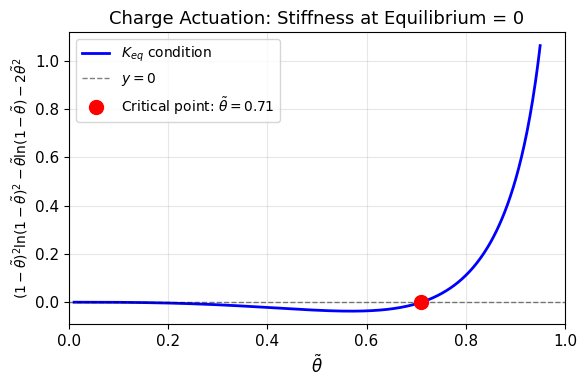
איור 1.10: הפתרון בצורה גרפית - הקשיחות בש”מ מתאפסת עבור .

ניתן לראות כי הקשיחות בש”מ מתאפסת עבור . מתוך תנאי ש”מ נקבל שעבור נקבל pull-in במערכת:

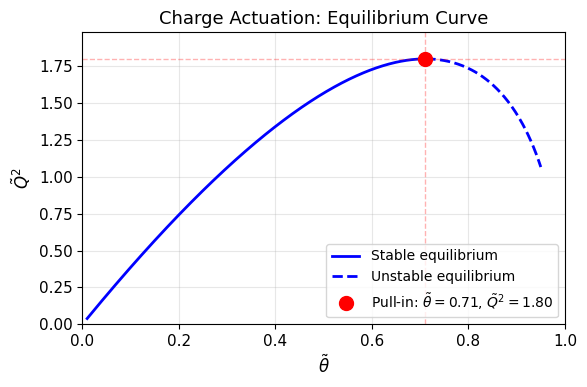
איור 1.11: עקומת שיווי המשקל - נקודת ה-pull-in מתרחשת עבור ו-.

עבור קבל מקביל קיבלנו שאין pull-in בהפעלת מטען, מה ההבדל כאן?

במשפעל לוחות מקבילים פילוג המטען אחיד על האלקטרודה, כמות מטען מסוימת נותנת מרחק מסוים. אם נזיז את האלקטרודה ממיקום ש”מ ונשחרר היא תחזור למקום המקורי.
במשפעל זוויתי פילוג המטען על האלקטרודה אינו אחיד - ככל שהקצה מתקרב לאלקטרודה התחתונה ריכוז המטען בו עולה. מכיוון שהקיבול אינו לינארי המומנט האלקטרוסטטי אינו לינארי ותתכן נקודה בה הוא יגבר על ערכו של המומנט המכאני (קפיץ לינארי).

הפעלת מתח

כמו בהפעלת מתח, כשלב ראשוני נמצא את האנרגיה הפוטנציאלית של המערכת:

נציב את הקיבול שמצאנו מקודם:

ננרמל:

נוודא שהביטוי עבור המתח המנורמל חסר יחידות:

נוודא שאכן זהו גודל מנורמל:

הביטוי המנורמל לאנרגיה:

נמצא את הכוח הריאקטיבי ע”י גזירה לפי דרגת החופש :

תנאי ש”מ :

נחשב את קשיחות המערכת ע”י גזירה נוספת לפי דרגת החופש:

נרצה להסתכל על הקשיחות במצב ש”מ. נציב את התנאי שקיבלנו לתוך הביטוי של הקשיחות:

סף היציבות מתקבל כאשר :

באופן גרפי:

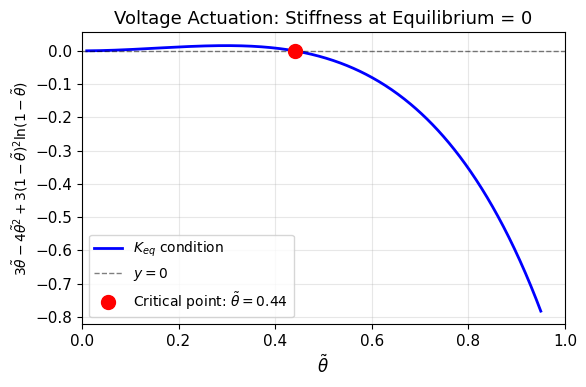
איור 1.12: הפתרון בצורה גרפית - הקשיחות בש”מ מתאפסת עבור .

ניתן לראות כי הקשיחות בש”מ מתאפסת עבור . מתוך תנאי ש”מ נקבל שעבור נקבל pull-in במערכת:

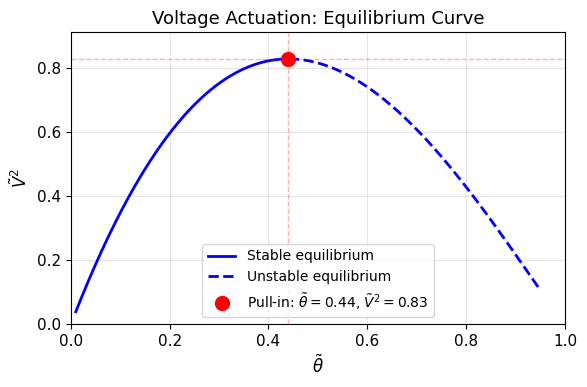
איור 1.13: עקומת שיווי המשקל להפעלת מתח - נקודת ה-pull-in מתרחשת עבור ו-.

נשים לב שעבור הפעלת מתח נקודת ה-pull-in מתרחשת בזווית קטנה יותר () לעומת הפעלת מטען ().

→ קודם: MCS1_000הבא: MCS1_002 ←