רזונטור דאפינג
איור 8.1: רזונטור לינארי חד-ממדי.
מה ההבדל בין רזונטור (resonator) לאוסילטור (oscillator)?
רזונטור היא מערכת שמקבלת אות בתדר הרמוני מסוים ומפיקה בחזרה אות באותו תדר, אך בהגברה. לעומת זאת, אוסילטור היא מערכת שמספקים אליה אנרגיה ומקבלים בחזרה אות בתדר הטבעי של המערכת. ההבדל המהותי הוא שבאוסילטור לא מספקים תדר, אלא רק אנרגיה - גם אם נספק לו אנרגיה בתצורת תדר מסוים, האוסילטור יפיק אות בתדר הטבעי שלו בלבד. למעשה, אוסילטור הוא רזונטור שמופעל באופן שונה.
משוואת התנועה (נקראת משוואת דאפינג) של רזונטור דאפינג היא מהצורה:
כלומר, אנו כרגע עוסקים בקפיץ לא לינארי, עם קשיחות מסדר
נוכל לרשום את משוואה זו באופן אל-ממדי:
כאשר:
כאשר
אין פתרון אנליטי מדויקת למשוואה זו, אז נדרש לפתור אותה נומרית. אבל, אם נביט במשוואת דאפינג ללא ריסון:
נראה כי לה יש פתרון אנליטי.
דרך אחת לפתור אותה היא להביט בסך האנרגיה של המערכת:
כאן
או:
צד שמאל הוא רק פונקציה של
לאחר פתרון בעזרת אינטגרלים אליפטיים:
איך היצור הזה נראה?
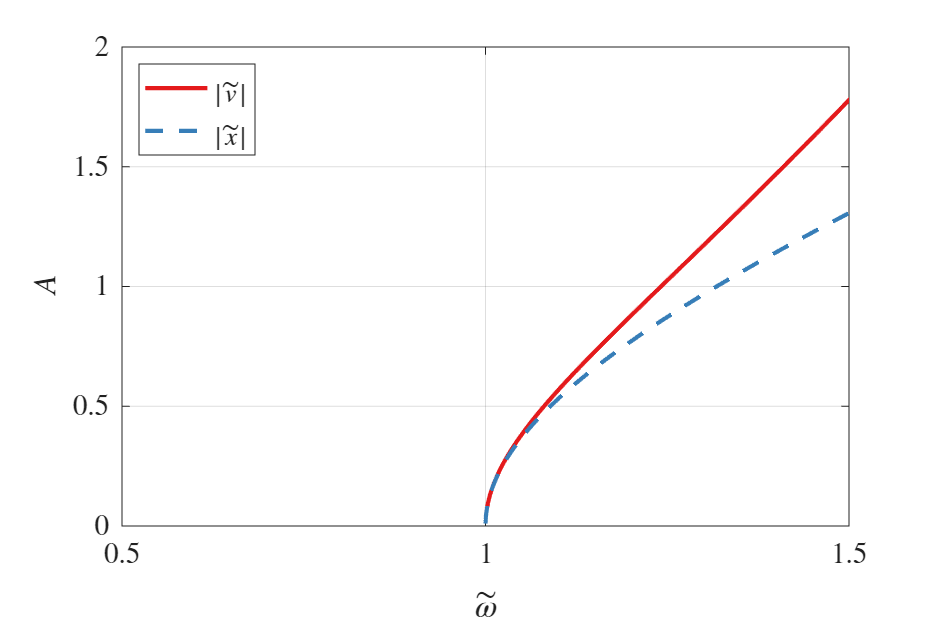
איור 8.2: “עמוד השדרה” של משוואת דאפינג. עמוד השדרה שונה עבור התגובה של ההזזה והתגובה של המהירות.
נזכור כי מדובר במקרה ללא ריסון!
באיור 8.2 אנו רואים שעבור תנאי התחלה, כלומר
מה קורה כאשר מוסיפים ריסון? כעת ניאלץ לחזור לחישובים נומריים - אבל עדיין נוכל לראות שעמוד השדרה מכתיב את צורת תגובת התדר של המערכת:
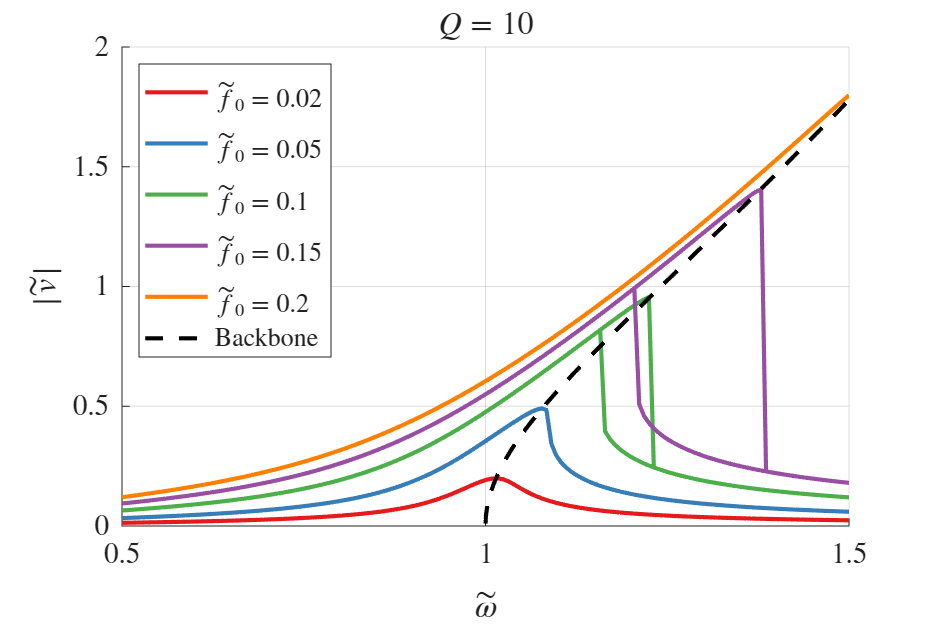
איור 8.3: תגובת התדר של משוואת דאפינג עבור ערכי
שונים.
נשים לב לתופעה מעניינת: בהפעלת כוח
כדי לקבל את איור 8.3 נומרית, ביצענו סריקת תדר (frequency sweep) בטווח
הבעיה היא שבמערכות לא לינאריות יכולים להיות מספר ענפים יציבים בו-זמנית. לכן, מריצים את הסריקה פעמיים:
- סריקה קדימה - מתדרים נמוכים לגבוהים.
- סריקה לאחור - מתדרים גבוהים לנמוכים.
כל כיוון סריקה “תופס” ענף אחר, וכך מקבלים את התמונה המלאה של תגובת התדר.

איור 8.4: תגובת הפאזה (של המהירות) של משוואת דאפינג.
כעת נסביר את הקפיצה בתגובת התדר באמצעות הפאזה. נתחיל מ-
- בתדרים נמוכים, המערכת נמצאת בפאזה חיובית (המהירות “מקדימה” את הכוח) עם אמפליטודה נמוכה.
- ככל שהתדר עולה, האמפליטודה גדלה והמערכת “נשארת” על הענף העליון של עקומת התגובה.
- כאשר מגיעים טיפה מעל לתדר הקריטי, הפאזה מתחילה להיות שלילית - הכוח מתחיל לפעול כנגד כיוון המהירות! הפתרון היציב היחיד בפאזה שלילית יהיה באמפליטודה נמוכה יותר - המערכת לא יודעת לתנוד באמפליטודה כל כך גבוה כאשר הכוח פועל כנגד כיוון המהירות.
כאשר מבצעים סריקת תדר לאחור (מתדרים גבוהים לנמוכים):
- בתדרים גבוהים, המערכת נמצאת בפאזה שלילית עם אמפליטודה נמוכה.
- ככל שהתדר יורד, האמפליטודה גדלה בהדרגה - המערכת עוקבת אחר הענף התחתון.
- כאשר מגיעים טיפה מתחת לתדר הקריטי, הפאזה מתחילה להיות חיובית - הכוח מתחיל לפעול עם כיוון המהירות! הפתרון היציב היחיד בפאזה חיובית הוא באמפליטודה גבוה יותר - המערכת לא יודעת לתנוד באמפליטודה כל כך נמוכה כאשר הכוח פועל עם כיוון המהירות.
תרגילים
שאלה 1
נתון משפעל מסרק דו-צדדי (double sided comb drive), המחובר לקפיץ מכאני לינארי. הרוטור הינו בעל
נתון כי מהלך התנועה הינו
איור 8.5: מערכת מסרק דו-צדדי.
פתרון:
נתחיל בחישוב קיבול שקול של המערכת.
במצב ההתחלתי (כאשר
מספר השיניים בממוצע בצד שמאל וצד ימין של הרוטור הינו:
נשים לב שמאחר ומספר השיניים הוא בדיד, כאשר סוכמים את מספר השיניים החופפות יכולים לקבל מס’ שיניים לא שלם.
אורך החפיפה הממוצע בצד שמאל וצד ימין של הרוטור הינו:
לכן הקיבול של צד שמאל וצד ימין הינם בהתאמה:
כאשר
הקבלים מחוברים במקביל לכן הקיבול הכולל הינו סכום פשוט. פתיחת סוגריים וכינוס איברים ייתן לנו:
לכן החלק ה-אלקטרוסטטי של האנרגיה הפוטנציאלית:
החלק ה-אלקטרוסטטי של הכוח הריאקטיבי:
החלק ה-אלקטרוסטטי בקשיחות המערכת הינו:
כלומר יש לנו קשיחות אלקטרוסטטית שאינה תלויה בהזזה אלא רק בריבוע המתח (גם עבור הזזות גדולות). משמע משוואה שולטת של מבנה זה היא:
התדירות העצמית הינה:
תכונה זו (האפשרות להשפיע על פרמטרי המערכת, בעיקר על הקשיחות) במערכות מיקרו-מכאניות, מאפשר תכנון של התקנים עם תדירות עצמית משתנה יחסית בקלות. חופש זה מאפשר הם פיצויי על שגיאות ייצור, הרחבת תחום עבודה (חישה בתדרים שונים), התאמת תדרים במערכות מרובות דרגות חופש וכו’.
בנוסף, במקרה שבו מתח הכוונון משתנה בזמן (במקום
