פנגייה

MDN1_002 כשלים כתוצאה מעומס משתנה

• זמן קריאה: 19 דק'

מבוא להתעייפות

בפרק קודם עסקנו בניתוח ועיצוב חלקים הנתונים ללחץ סטטי. כעת, נעבור להתעייפות - כשל כתוצאה מעומס משתנה.

לפני המאה ה-19, תיכון מכני התבסס בעיקר על עומסים סטטיים. העומסים היו נמוכים יחסית, מקדמי הביטחון היו גדולים, המהירויות היו די איטיות. ברגע שהומצא מנוע הקיטור, בעיות החלו לצוץ. גלים היו צריכים להסתובב מהר יותר, ובכך חוו מחזורים דינמיים רבים ומהירים יותר. חלק מהכשלים הראשונים כתוצאה ממחזורים אלו היו פסי רכבת באמצע המאה ה-19, מה שהוביל לחקר עמוק של הכשלים - משם התפתחו הרעיונות הראשונים לכשל התעייפות.

היווצרות סדק והתקדמותו

כשל התעייפות נוצר כתוצאה מהיווצרות סדק והתקדמותו. הוא יתחיל בנקודה שחווה מאמצים מחזוריים גבוהים (ולפיכך גם עיבורים גבוהים). נקודה זו נמצאת בדרך כלל בנקודות אי-רציפות בחומר, כמו למשל חריצים, חורים, שינויים בשטח חתך, שינויים במבנה החומר וכו’.

ניתן לסווג כשל התעייפות בשלושה שלבים:

כשל התעייפות בבורג כתוצאה מכיפוף חוזר. (Budynas et al., 2015).

השלב הראשון הוא תחילת סדק או מספר סדקים כתוצאה מדפורמציה פלסטית. סדקים בשלב זה לרוב לא ניתנים להבחנה בעין בלתי מזוינת. בשלב השני הסדקים מתפתחים לסדקים גדולים היוצרים סדקים מישוריים מקבילים שמופרדים ע”י “רכסים” אורכיים. המישורים לרוב חלקים ומאונכים לכיוון של המאמץ המקסימלי. משטחים אלו מאופיינים ע”י רצועות בהירות וכהות שנקראות קווי חוף. במהלך עומס מחזורי, משטחי הסדקים נפתחים ונסגרים, מתחככים אחד עם השני, וקווי החוף משנים את תצורתם כתלות בשינויים ברמת או תדירות העומס. השלב שלישי מתרחש במחזור העמסה האחרון כאשר השטח חתך לא יכול לתמוך יותר בעומסים, מה שגורם לשבר פתאומי ומהיר. השבר בשלב השלישי יכול להיות פריך, משיך, או שילוב של שניהם.

שיטות לחישוב עמידות תכן

שלושת השיטות הראשיות לחישוב עמידות תכן מסוים בפני כשל התעייפות הן שיטת stress-life, שיטת strain-life, ושיטת linear-elastic fracture mechanics (LEFM) - או פשוט שיטת מכניקת השבר. שיטות אלו באות לחזות את “חיי” התכן כתלות במספר המחזורים לשבר, , לרמת העמסה מסוימת. בגדול, שיטת strain-life מתמקדת בהיווצרות הסדק (שלב ראשון), שיטת מכניקת השבר מתמקדת על התקדמות השבר (שלב שני), ושיטת stress-life ממזגת את כל שלושת השלבים בעזרת נתונים אמפיריים (ניסויים).

כאשר העומסים המחזוריים יחסית נמוכים, המאמצים והעיבורים לרוב אלסטיים, וחיי התכן ארוכים (בדרך כלל, יותר מ- או ), אזור זה נקרא high-cycle fatigue. מצד שני, עבור עומסים מרובי מחזורים, עם מאמצים ועיבורים פלסטיים, וחיי תכן קצרים, האזור נקרא low-cycle fatigue.

שיטת Stress-Life ועקומת S-N

שיטת stress-life מסתמכת על מחקרים על דגמים הנתונים למאמצים מחזוריים בין שתי רמות מאמצים מחזוריים, מה שנקרא העמסה באמפליטודה קבועה (constant amplitude loading). המכשיר הכי נפוץ לבדיקות התעייפות נקרא ה- R.R. Moore high-speed rotating-beam machine. מכשיר זה מפעיל על הדוגמה כפיפה טהורה (ללא גזירה) ע”י משקלים. הדוגמה, שהגאומטרייה שלה מתוארת באיור הבא, מעובדת ומלוטשת בזהירות רבה כדי למנוע שריטות היקפיות.
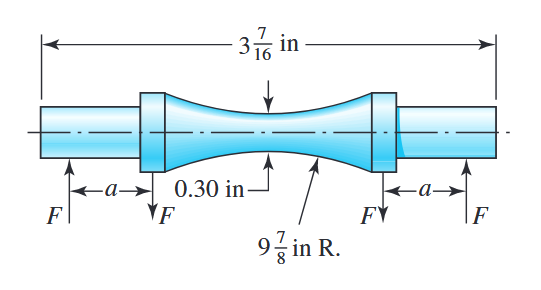
bookhue

גאומטריית דוגמה למכונת R. R. Moore rotating-beam. המומנט כפיפה אחיד, , לאורך העיקול, והמאמץ הכי גבוה נמצא באמצע הקורה. (Budynas et al., 2015).

כדי למצוא את חוזק ההתעייפות של חומר מסוים, נדרשים מספר בדיקות בגלל הטבע הסטטיסטי של התעייפות. לבדיקת כפיפה סובבת (rotating-beam), מפעילים כפיפה קבועה, ומודדים את מספר החזרות לכשל. תוצאות הבדיקה נרשמות על גרף שנקרא דיאגרמת/עקומת :
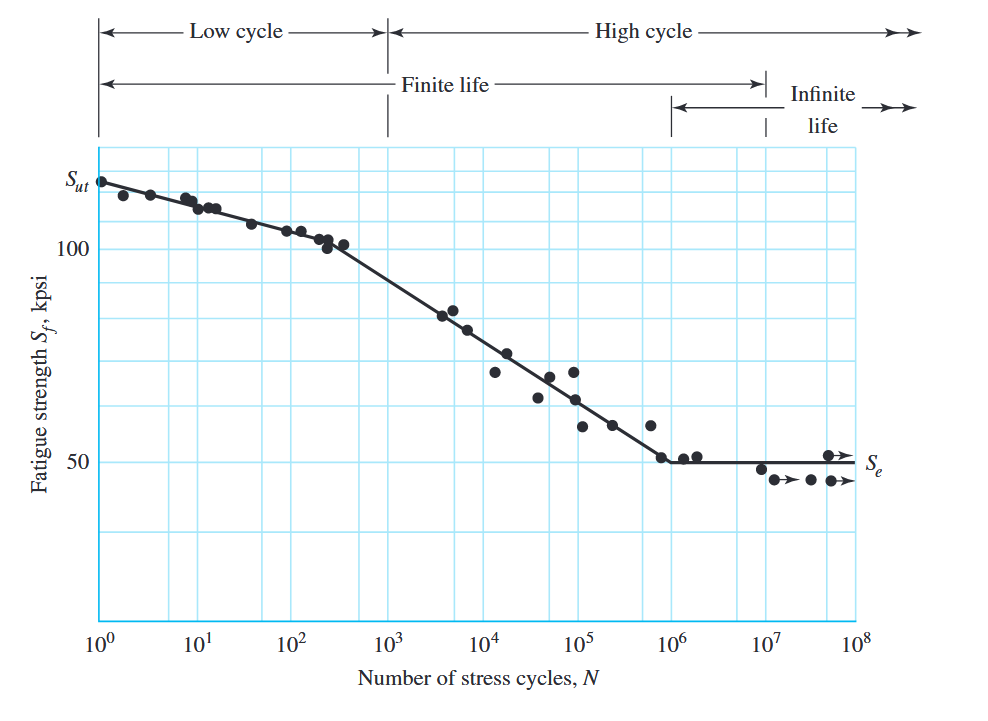
bookhue

דיאגרמת מתוצאות של בדיקות completely reversed axial fatigue על פלדת UNS G41300. מ-(Budynas et al., 2015).

ציר ה- של הגרף נקרא חוזק התעייפות , גודל חסר משמעות אם לא מצרפים אליו את מספר החזרות אליו הוא מתאים.
במקרה של מתכות וסַגְסוֹגוֹת בַּרְזִלִּיּוֹת, הגרף נהיה אופקי לאחר שהחומר הועמס במספר מסוים של חזרות. הנקודה בה אופקיות זו מתחילה נקראת “ברך”, והמאמץ המתאים לה נקרא גבול הסיבולת (endurance limit) , או גבול/סף ההתעייפות (fatigue limit). הדיאגרמה הזאת אף פעם לא נהיית אופקית עבור מתכות וסגסוגות לא ברזליות, ולכן אין להם סף התעייפות. הגרף הבא מתאר את דיאגרמת לרוב הסגסוגות אלומיניום. מאחר ואין לאלומיניום סף התעייפות, נהוג להגדיר מספר סופי של מחזורי אורך חיים של החלק (לאלומיניום, נהוג להגדיר ) וקובעים את החוזק להתעייפות כסף להעמסה.
bookhue

דיאגרמות המייצגים סגסוגות אלומיניום שונות. (Budynas et al., 2015).

הדיאגרמות מתקבלות ממחזורי מאמצים מהופכים לחלוטין (completely reversed), בהם גודל המאמץ מתחלף בין גדלים שווים של מתיחה ולחיצה.

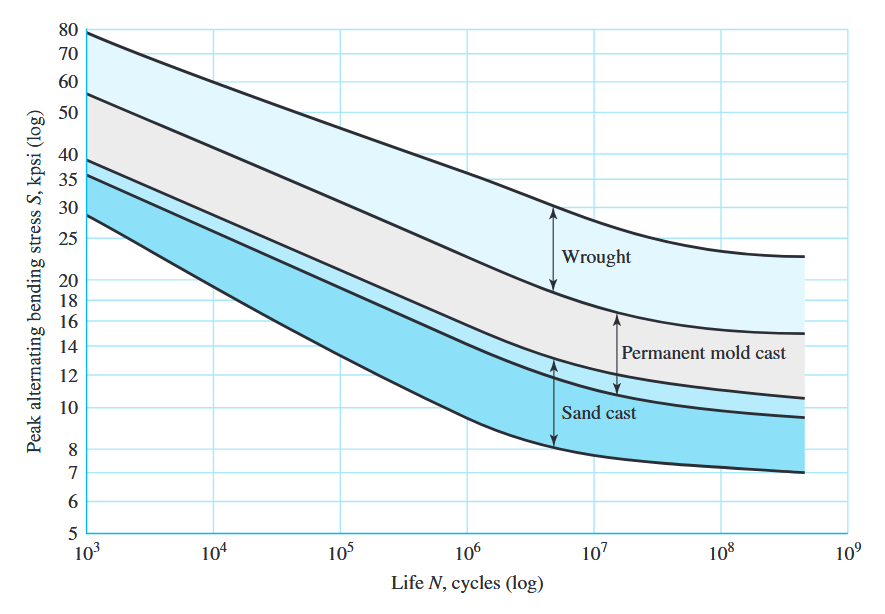
קביעת הסף התעייפות ע”י בדיקת התעייפות היא תהליך אורך. בשלבי האב-טיפוס ואפילו לפעמים גם בחלק מניתוחי כשלים משתמשים בשיטה מהירה יותר לאמוד את ספי ההתעייפות. הגרף הבא מתאר מספר רב של בדיקות כפיפה סובבת ובדיקות מתיחה פשוטות של דוגמות מאותו המְטִיל:

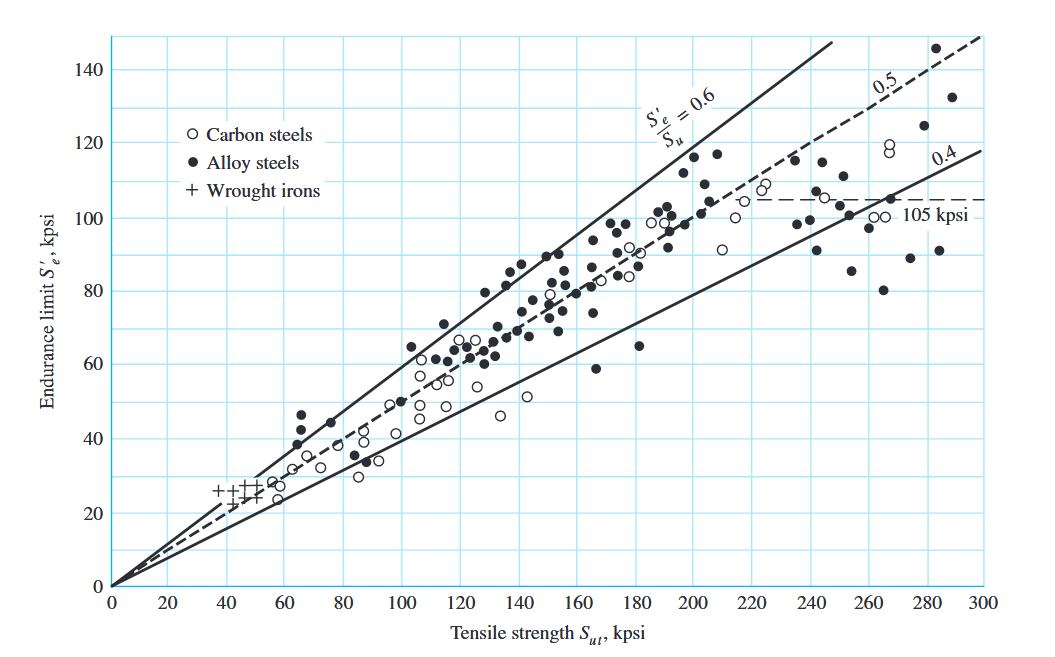
bookhue

גרף של ספי ההתעייפות לעומת חוזק מתיחה מבדיקות על מספר גבוה של ברזלים מחושלים ופלדות. (Budynas et al., 2015).

ניתן לראות שיש איזשהו מִתְאָם בין שני הסוגים השונים של הבדיקות. הגרף מראה שיש שהסף התעייפות מתרחש בערך בין ל- מהחוזק מתיחה לפלדות עד בערך (). מ- , הפיזור גדל, אבל נדמה כי המגמה מתיישרת, כפי שניתן לראות לפי הקו המקווקו האופקי ב- .

עבור פלדות, כדי לפשט את התוצאות בגרף לעיל, אנו נניח שספי ההתעייפות הם:

כאשר הוא החוזק המתיחה המינימלי. התג () על מדגיש את העובדה שמדובר על דוגמת כפיפה סובבת. את הסימון נשמור לסף ההתעייפות של החלק בו אנו מעוניינים לתכן, שיכול להיות מאוד שונה (נראה עוד מעט).
לפלדות שעברו טיפול כלשהו לקבלת מיקרו-מבנים שונים יש יחסי שונים. נדמה כי למיקרו-מבנים גמישים יש יחס יותר גבוה. מרטנזיט הוא מאוד פריך ורגיש לכשלי התעייפות; לפיכך, היחס שלו נמוך.
את החוזקי התעייפות של החומרים השונים ניתן לראות בטבלה A24.

חוזק התעייפות

כפי שראינו בגרף הראשון, התעייפות low-cycle היא בטווחים בין ל- מחזורים. באזור זה, החוזק התעייפות קטן במעט מהחוזק מתיחה .
עבור פלדות, קירוב די טוב לקשר זה ב- low-cycle הוא מהצורה:

כאשר:

כאשר הוא החוזק להתעייפות ב- (בספר, מסומן כ- ). היחס בין ל- מסומן ב- ונקרא שבר חוזק התעייפות (fatigue strength fraction), כך ש:

בהיעדר נתונים, עבור פלדות, מומלץ לשלוף את מהגרף הבא:
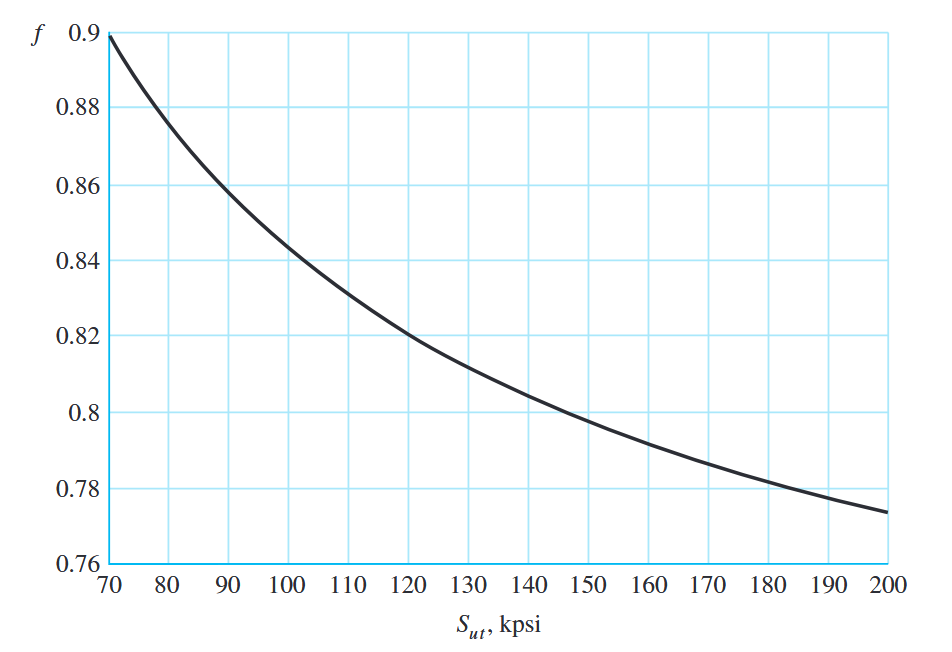
bookhue

שבר חוזק התעייפות, , של ב- מחזורים עבור ב- מחזורים. (Budynas et al., 2015).

באופן, שקול נוכל לרשום את המקדמים באופן הבא:

עבור high-cycle, המשוואה עבור עדיין תקפה, אך הפעם המקדמים:

או, באופן שקול (שרשום בספר):

בהינתן מאמץ מהופך לחלוטין , נוכל להציב ב-(SH6-13) כדי לקבל את מספר המחזורים לכשל התעייפות:

מקדמי מארין לסף התעייפות

ראינו שהדוגמת כפיפה-סובבת במעבדה עוברת תהליך מאוד קפדני לפני שמבצעים עליו את הבדיקות, שמתרחשות בתנאי מעבדה. לכן, לא נצפה שהתוצאות עבור התכן שלנו, תחת אילוצים מציאותיים, יהיו זהות.
לכן, מספר מקדמים הוגדרו שיתקנו את ה- של תנאי המעבדה ל- לתכן שלנו - הסף התעייפות ב”תאכלס”. מקדמים אלו מופיעים במשוואת מארין (Marin):

נוסחה: משוואת מארין

כאשר:

  • המקדם הוא מקדם תיקון לטיב פני השטח.
  • המקדם הוא מקדם תיקון לגודל.
  • המקדם הוא מקדם לצורת העמיסה.
  • המקדם הוא מקדם תיקון לטמפרטורה.
  • המקדם הוא מקדם תיקון לאמינות.
  • המקדם הוא מקדם תיקון כללי.

מקדם תיקון לטיב פני שטח

הפני שטח של דוגמת כפיפה סובבת הוא חלק מאוד. המקדם תיקון לטיב פני שטח תלוי באיכות של פני השטח של החלק האמיתי ובחוזק המתיחה של אותו חלק:

כאשר הוא החוזק מתיחה המינימלי ו- ו- ניתנים למציאה מטבלה 6-2.

מקדם תיקון לגודל

עבור כפיפה ופיתול, נמצא כי המקדם תיקון לגודל הוא:

כאשר הוא קוטר החלק.

משוואה (SH6-20) פותחה עבור מוט שהוא במצב כפיפה סובב. כלומר, נקודות על החתך שלו הנמצאים במרחק שווה מציר הסיבוב חווים מאמץ זהה. אבל מה קורה אם המוט במצב כפיפה לא סובב, או כאשר החתך לא עגול?
במקרה זה, הגישה להשתמש בקוטר שקול (equivalent) ולהציב אותו במקום ה- ב-(SH6-20). את מקבלים ע”י השוואה בין הנפח של חומר תחת מאמץ ב-, ומעל, מהמאמץ המקסימלי של אותו הנפח בדוגמת כפיפה סובבת.

שטח מאמץ .

נמצא כי כאשר שני הנפחים מושווים, האורכים מתקזזים, כך שנוכל להתחשב רק בשטח החתך. לחתך סובב עגול, השטח מאמץ שלו הוא השטח בטבעת עם קוטר חיצוני וקטור פנימי של . נסמן את גודל זה ב- ונקבל:

כעת, עבור השטח חתך של החלק שלנו אנו מחשבים את הרלוונטי אליו, משווים ל-(SH6-22), ונקבל את הקוטר האפקטיבי שלו. טבלה 6-3 מספקת גדלי של צורות מבניות החווות כפיפה לא סובבת.

עבור מתיחה צירית אין השפעה לגודל, אז:

מקדם תיקון להעמסה

אומדנים שונים לספי העמסה לרוב מתקבלים מבדיקות של העמסות מהופכות לחלוטין. עם העמסה צירית או פיתולית, בדיקות ההתעייפות מעידות על יחסים שונים בין ספי ההתעייפות והחוזק לכל סוג של העמסה. נוכל להתייחס לשוני זה עם מקדם תיקון באופן הבא:

כאשר ההעמסה מעורבת (שילוב של כמה צורות העמסה), נשתמש ב:

ונתייחס להעמסות אלו ע”י שיטה אחרת שנסביר בהמשך.

מקדם תיקון לטמפרטורה

כאשר פועלים בטמפרטורות הנמוכות מטמפרטורת החדר, יש סיכוי גבוה לסדק פריך, שהוא כבר כשל שצריך לחקור אותו קודם, ואז לגשת לניתוחי התעייפות. כאשר פועלים בטמפרטורות הגבוהות מטמפרטורות החדר, צריך לחקור קודם כשלי כניעה כי חוזק הכניעה יורד משמעותית עם עלייה בטמפרטורה. כל מאמץ יַשְׁרֶה גם זחילה בחומר הפועל בטמפרטורות גבוהות, אז צריך להתחשב גם בזה. לבסוף, יכול להיות שלא יהיה סף התעייפות לחומרים הפועלים בטמפרטורות גבוהות.
מכמות המידע המוגבלת שיש לנו על השפעת הטמפרטורה על חומרים, אנו יודעים שסף ההתעייפות לפלדות עולה מעט כאשר הטמפרטורה עולה, ואז מתחיל ליפול באזור ה-, באופן מאוד דומה להתנהגות של חוזק מתיחה:
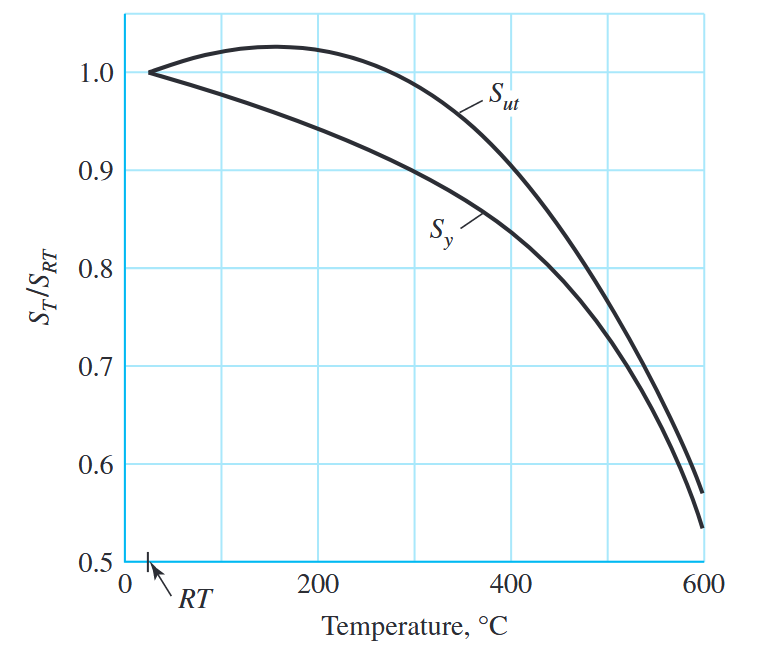
bookhue

שרטוט של התוצאות של 145 בדיקות על 21 סגסוגות פלדה המציגים את ההשפעה של טמפרטורה על מאמץ הכניעה והחוזק . ( הוא חוזק המתיחה בטמפרטורה הנתונה, הוא החוזק מתיחה בטמפרטורת החדר). (Budynas et al., 2015).

כיוון שהקשרים דומים זה לזה, נהוג להיעזר בגרף כדי להעריך את ההשפעה של טמפרטורה על סף ההתעייפות. נוכל להשתמש בטבלה 6-4 המוכנה מראש.

או, נוכל גם להשתמש בפולינום ממעלה רביעית שהותאם לגרף לעיל (עבור טמפרטורה הנתונה ב-):

כך או כך, מקדם התיקון לטמפרטורה יהיה:

מקדם תיקון לאמינות

למידע שהצגנו עבור פלדות - הטבלאות, הגרפים, יש רמת פיזור כלשהי - הוא כמובן לא אמין. רוב המידע שהוצג נלקח בממוצע. נמצא כי הסְטִיַּת תֶּקֶן (standard deviation) של הבדיקות שנעשו לא עולה על . לכן, נוכל לחשב את מקדם התיקון לאמינות כ:

כאשר נתון ע”י טבלה 6-5, כתלות ברמת האמינות שאנו דורשים.

מקדם תיקון כללי

עם מקדם זה מדובר בתופעות נוספות שמורידות את הסף להתעייפות. למשל:

  • מאמצים שיוריים עלולים להשפיע לחיוב או לרעה על סף ההתעייפות.
  • קורוזיה - שִׁתּוּךְ חִכּוּכִי (fretting corrosion).
  • ציפויים אלקטרוליטיים כמו ציפוי כרום, ניקל וכו’ עלולים להוריד את סף ההתעייפות עד כ-.
  • תדר ההעמסה - תחת תנאים נורמליים, כשל התעייפות לא תלוי בתדירות ההעמסה. אבל, אם מתרחשת קורוזיה, או שמדובר בטמפרטורות גבוהות, קצב המחזור הופך להיות קריטי. ככל שהתדירות יותר נמוכה והטמפרטורה עולה, קצב התקדמות הסדק עולה ואורך חיי התכן יורד.

ריכוז מאמצים ורגישות חריץ

אנו יודעים כבר שכאשר יש אי-רציפויות בגאומטרייה כמו חורים, חריצים, מגרעות וכו’, המאמץ שעלול להתפתח באזורם גדל משמעותית. השתמשנו במקדמי ריכוז מאמצים ו- כדי להתחשב אי-רציפויות אלו. נמצא כי חלק מהחומרים לא רגישים כל כך לקיום חריצים בגאומטרייה שלהם, כך שעבורם ניתן להשתמש בערך מונמך של . לחומרים עלו, המאמץ האפקטיבי המקסימלי להתעייפות הוא:

כאשר הוא ערך מונמך לערך של ו- הוא המאמץ הנומינלי. ל- אנו קוראים מקדם ריכוז מאמצים להתעייפות (fatigue stress-concentration factor), ולכן הוא מסומן ב-. ניתן לחשוב עליו באופן הבא:

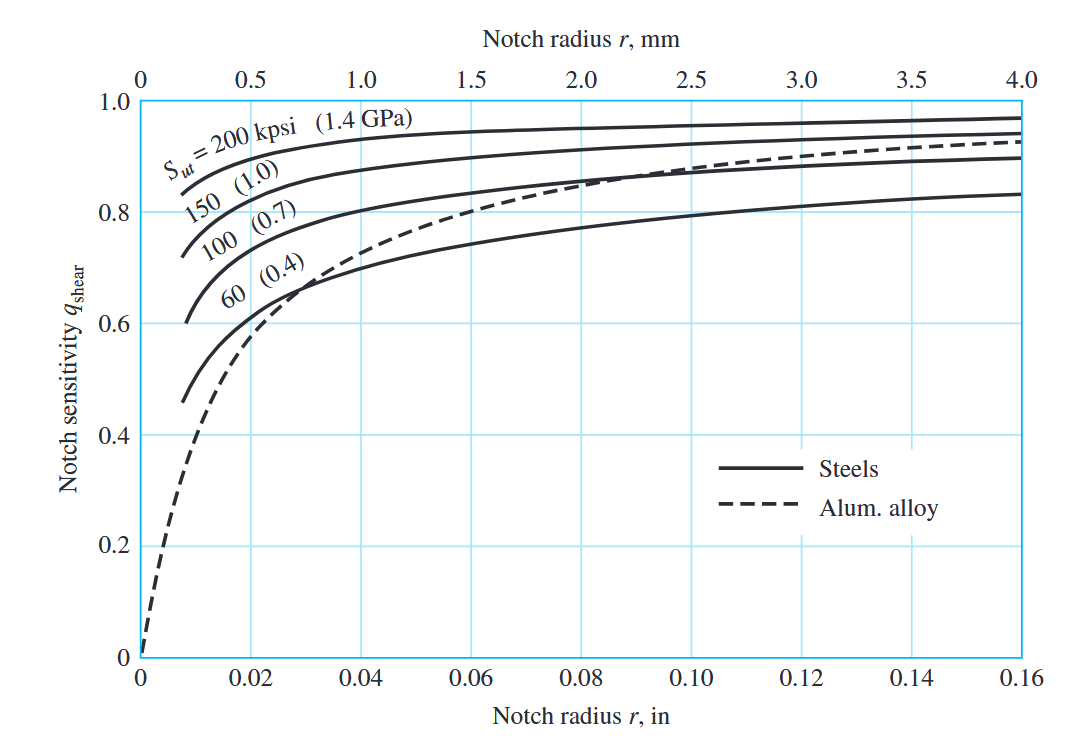
הרגישות חריץ מוגדרת ע”י המשוואה:

כאשר הערך של נע בין ל-. ניתן לראות מהמשוואה לעיל שאם אז , ולחומר אין רגישות לחריצים בכלל. מנגד, אם , אז , ולחומר יש רגישות לחריצים מלאה.
רגישות לחריץ הוא ערך שתלוי בחומר, והוא אמפירי. עבור פלדות ואלומיניום, ניתן למצוא אותו מהגרף הבא:
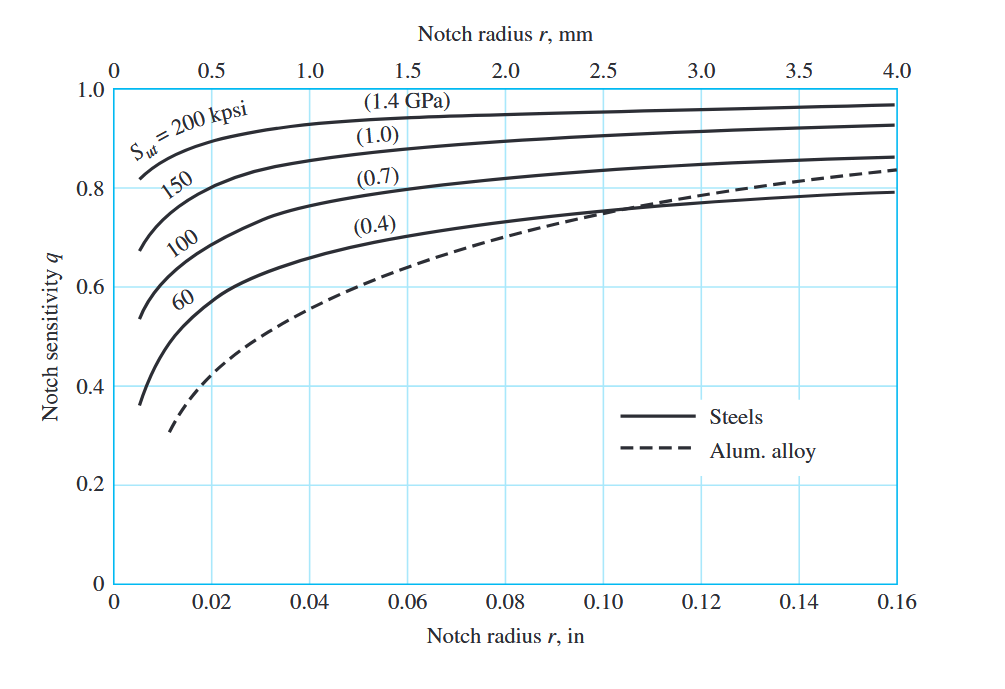
bookhue

עקומות רגישות לחריץ לפלדות ו- UNS A92024-T אלומיניום חשיל הנתונים ל-כפיפה בהיפוך או עומס צירי בהיפוך. (Budynas et al., 2015).

bookhue

עקומות רגישות לחריץ לפלדות ו- UNS A92024-T אלומיניום חשיל הנתונים ל-פיתול בהיפוך. (Budynas et al., 2015).

סיווג מאמצים תונדים

מאמצים תונדים במכונות לרוב בצורה סִינוּסוֹאִידִית מטבע אופן הפעולה של רוב המכונות הסובבות. אבל, תנודות אחרות גם כן עלולות להתרחש. נמצא שבמאמצים מחזוריים, הצורה של הגל פחות חשובה מאשר הערכים בקיצון של הגל. לכן, מספיק להשתמש ו- במחזור כוח כלשהו כדי לאפיין את הכוח. נסמן את הכוח הממוצע ואת האמפליטודה של הכוח ב:

באותו אופן נגדיר גם עבור מאמצים:

האיור הבא מכיל גרפים של סוגים שונים של מאמצים חוזרים. הגדלים בגרפים המוצגים הם:

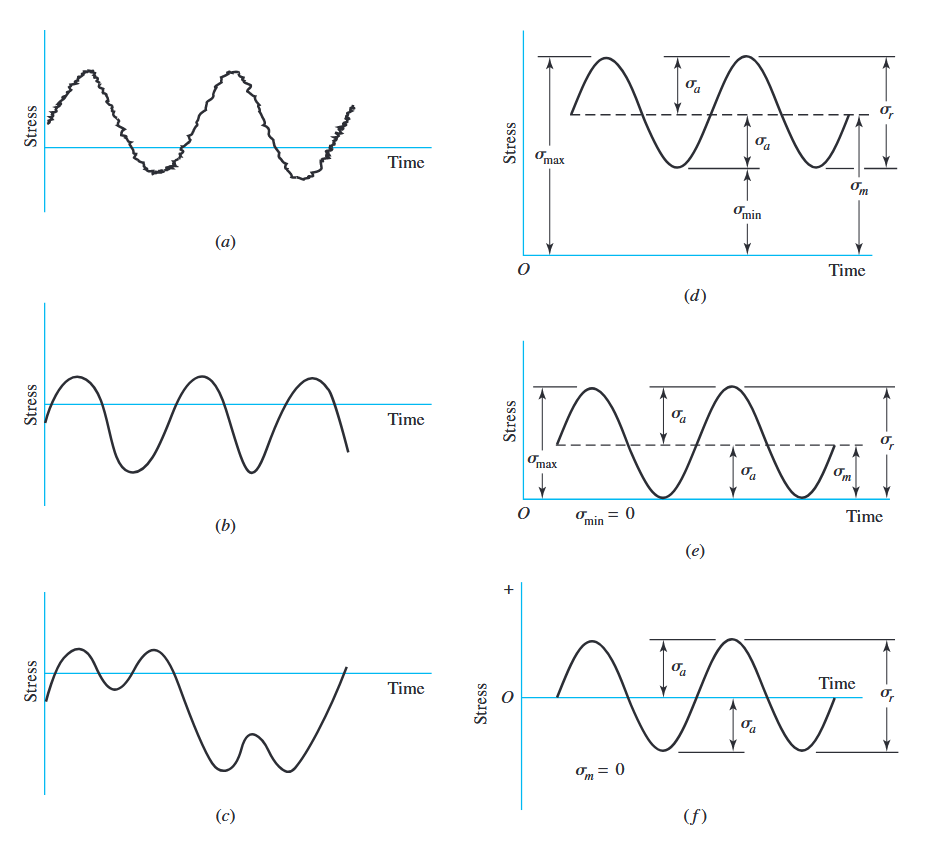
bookhue

מספר קשרי מאמץ זמן: (a) מאמץ תונד עם תדירות גבוהה רועדת. (b ו-c) מאמץ בתנודות לא סינוסואידיות. (d) מאמץ תונד סינוסויאידית. (e) מאמץ חוזר. (f) מאמץ מהופך לחלוטין סינוסואידית. (Budynas et al., 2015).

כאשר נרצה לחשב את המאמצים עם ריכוז מאמצים, נפריד בין חומרים פריכים וחומרים משיכים, שמתנהגים שונה ביחס לאזורים עם ריכוז מאמצים. בנוסף, נגדיר את הגדלים הנומינליים שהם אמפליטודת המאמץ והמאמץ הממוצע של התנודות ללא ריכוזי מאמצים.

עבור חומרים פריכים, פשוט נפעיל את מקדם הריכוז מאמצים על המאמצים הנומינליים כדי לקבל את המאמצים:

עבור חומרים משיכים, טוענים כי הוא עמיד יותר בפני דפורמציה פלסטית באזור ריכוז המאמצים, ואף חוזקו עלול לעלות באזור זה לאור הקשיית מעוותים. לכן, אנו לא נתייחס אליו במקרה של המאמץ הממוצע:

במיידה והדפורמציה הפלסטית אינה מותרת ממגוון שיקולים (בטיחות, טולרנסים וכו’), נחמיר וניקח מקדם ריכוז מאמצים עבור המאמצים הממוצעים.

קריטריוני כשל להתעייפות בהטרחה מחזורית

כעת, לאחר שהגדרנו את המרכיבים השונים של מאמץ של חלק הנתון למאמץ תונד, נרצה לשחק טיפה עם הגדלים של המאמץ הממוצע ואמפליטודת המאמץ, כדי ללמוד משהו לגבי ההתנגדות להתעייפות של החלקים כאשר הם נתונים לסיטואציות כאלו. התוצאות לבדיקות כאלו מוצגות בגרף הבא:
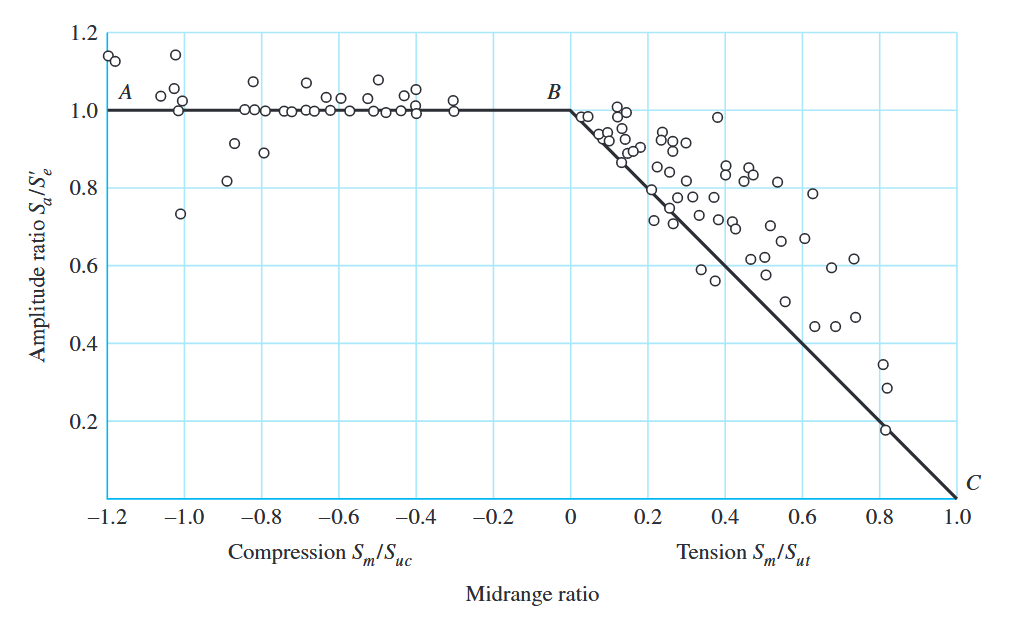
bookhue

גרף של כשלי התעייפות עבור מאמצים ממוצעים בלחיצה משמאל ומתיחה בימין. (Budynas et al., 2015). הוא חוזק הכניעה במתיחה (tension) ו- הוא חוזק הכניעה בלחיצה (compression).

כפי שניתן לראות, כאשר המאמץ הממוצע בלחיצה, כשל מתרחש כאשר או (כאשר הוא , בלחיצה - compression). עבור מתיחה, נצטרך כבר גרף אחר שייתן לנו קצת יותר מידע על איך להתמודד עם מצבים אלו:
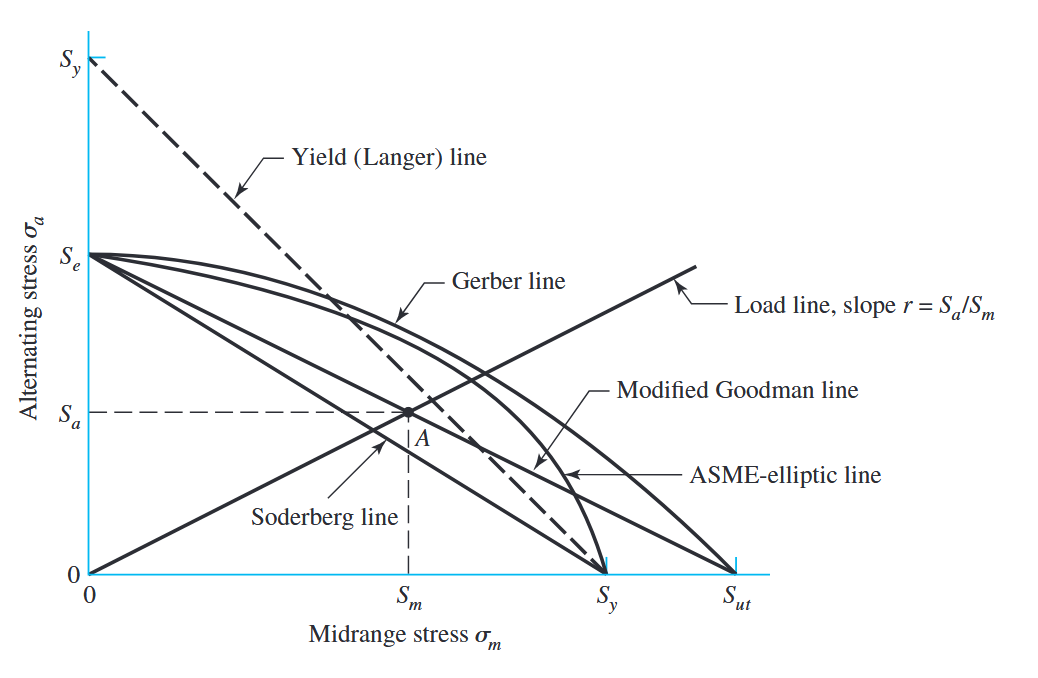
bookhue

גרף התעייפות המראה קריטריונים שונים לכשל. לכל קריטריון, נקודות על או “מעל” הקו הרלוונטי מתאר כשל. (Budynas et al., 2015).

בגרף לעיל מתוארים חמישה קריטריונים שונים לכשל התעייפות, כולם טוענים שיש שילובים מסוכנים ושילוב בטוחים של ו-.
נשים לב הציר האנכי מייצג את שכבר מתוקן ע”י מקדמי מארין לסף התעייפות. בנוסף, גם נמצא על הגרף, כי חלק מהקריטריונים מסתמכים גם עליו כדי להתחשב בסיכוי של כניעה כבר במחזור מאמץ הראשון.

מבחינת המשוואות לקריטריונים השונים:

כאשר הוא מקדם הביטחון.

נוכל בעזרת הקריטריונים גם לחשב את חוזק ההתעייפות. למשל, בעזרת קריטריון גודמן, אם , נחליף את במאמץ להיפוך מוחלט :

כעת נוכל להציב במשוואה (SH6-16) כדי לקבל את מספר המחזורים להתעייפות. חשוב לזכור לאפיין אם מדובר ב-LCF או HCF כדי להציב את המקדמים ו- הרלוונטיים.

שימו לב!

תמיד תמיד כאשר מבקשים מקדם ביטחון גודמן, תמיד תמיד לחשב גם את לנגר, אחרת מאור יעיף עליך שולחן. לנגר נותן מקדם ביטחון לכניעה כבר במחזור הראשון, מה שגודמן לא מתייחס אליו.

חוזק התעייפות לפיתול תחת מאמצים תונדים

מתוך 72 ניסויים ע”י אח שלנו James O. Smith, ניתן לראות שלחוזק הכניעה לפיתול אין השפעה על סף ההתעייפות לפיתול, כל עוד החומר הוא משיך, מלוטש, ללא חריצים, ובצורת גליל.
התוצאה השנייה שהוא קיבל תקפה לחומרים עם ריכוזי מאמצים. במקרה זה הוא מצא שהסף התעייפות יורד מונוטונית עם המאמץ פיתול באופן הבא:

כעת, כאשר אנו מציבים ערכים בקריטריונים השונים, עלינו להציב את המאמצים הרלוונטיים לפיתול. לכן, נציב ו- במקום ו-. נזכור גם שמאחר ומדובר בפיתול, נצטרך להציב גם עבור . בנוסף, נציב את במקום וגם וגם וגם נחליף את עם שזה כבר לפי פון-מיזס. לדוגמה, הקריטריון mod-Goodman עבור פיתול יהיה:

שילוב תצורות העמסה

במקדם תיקון להעמסה ראינו איך לטפל בבעיות בהן יש תצורה העמסה אחת - צירית, כפיפה או פיתול. כעת נעבור על מה עושים כאשר יש שילוב של תצורות ההעמסה השונות.
נמצא כי שיטות האנרגיה של פון-מיזס עובדות יחסית טוב גם עבור כשלי התעייפות כאשר מדובר בחומר משיך תחת מאמצים שונים.
הצעד הראשון הוא לחשב שני גדלי מאמצים - אחד למאמצים המתחלפים והשני למאמצים הממוצעים . נפעיל את מקדמי המאמצים המתאמים לכל אחד מהמאמצים (למשל, למאמצי כפיפה). לאחר מכן, נחשב את המאמץ השקול לפי פון-מיזס לכל אחד מהמאמצים ו-’. לבסוף, נבחר קריטריון כשל (mod-Goodman, Gerber וכו’).
לא נשתמש במקדם התיקון לפיתול כי כבר מתייחסים אליו בחישוב למאמץ פון-מיזס. למקדם תיקון למאמץ צירי נוכל להתחשב ישירות כבר בחישוב של ו- ע”י חילוקו ב-.
כל התחשבויות אלו ניתנות לביטוי במאמצים השקולים:

הערות:

  1. יכולים להיות שונים למתיחה וכפיפה כיוון שיכול להיות שונה למתיחה וכפיפה.
  2. עבור חומרים משיכים, בחישוב המאמץ הממוצע , הערכים (או ) שווים ל-, לפי סיווג מאמצים תונדים.

כעת את הערכים השקולים ו- ניתן להציב בקריטריוני כשל.

נזק מצטבר בהתעייפות

בפועל, מקור העומס יכול להיות בעל עוצמה משתנה ותדרים שונים. איזה מהתדרים משמעותי, מה נחשב כמחזור, ומהו הנזק שנגרם כתוצאה מכך?
נביט במחזור מהופך לחלוטין עם מאמצים משתנים ו-, ועוד מחזור מהופך לחלוטין ו-. כפי שמוצג באיור הבא:
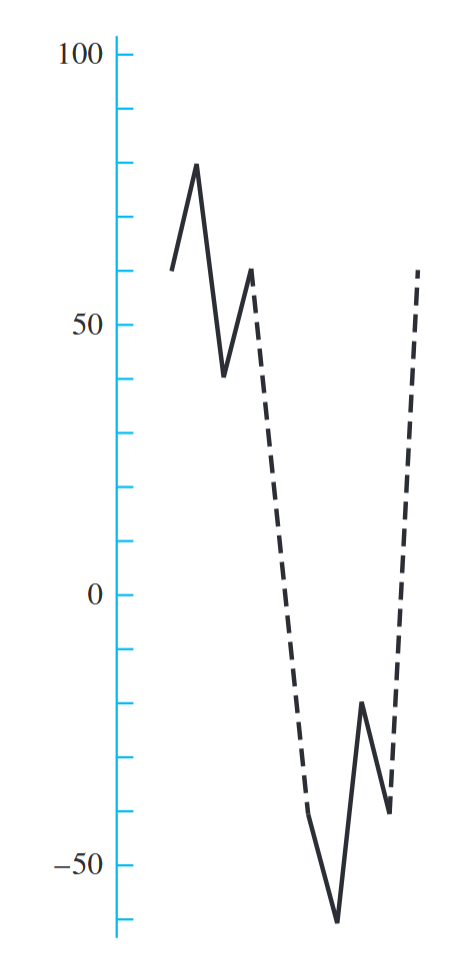
bookhue

דיאגרמה של מאמץ משתנה. הקו המקווקו נועד כדי “להדביק” את שני המחזורים ביחד אחד אחרי השני. (Budynas et al., 2015).

נרצה לגלות מחזור “נסתר”, שמתחיל ב- ונגמר ב- כפי שמוצג בגרף הבא:
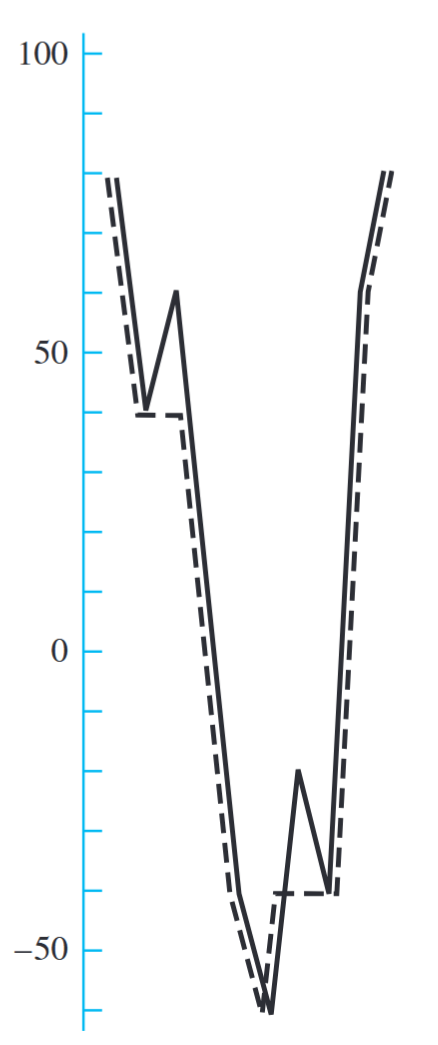
bookhue

דיאגרמה של מאמץ משתנה עם המחזור ה”מוסתר” שלו. (Budynas et al., 2015).

בניתוח המחזורים של המאמצים נאפיין כל מחזור “מוסתר” כזה כבלוקים.
נאמר ש:

  • המספר הוא מספר החזרות של בלוק כל אורחות החיים.

בתוך כל בלוק יש מספר מחזורים שונים, שחלק מהמחזורים האלו יכולים להופיע כמה פעמים באותו המחזור.

  • נסמן ב- את המאמצים של מחזור כלשהו.
  • נסמן ב- את מספר המחזורים שלו בתוך בלוק יחיד (אם המחזור חוזר פעמיים בתוך בלוק יחיד, אז ).

לכל קבוצת עומס יש את המספר מחזורים שלה לכשל:

  • נסמן ב- את מספר המחזורים לכשל של הקבוצה .

חוק מיינר קובע שכשל יתרחש כאשר:

כאשר הוא מספר המתקבל מניסויים והוא לרוב בין . ל- אנו קוראים הנזק המצטבר.

תרגילים

תרגיל 1

נתון המוט המתואר בציור:

הכוח והמומנט תונדים ללא הפרש פאזה ביניהם באופן:

החלק עשוי פלדה עם התכונות הבאות:

החלק מיוצר בחריטה.

סעיף א’

עבור אמינות של ומקדם ביטחון לפי גודמן לאורך חיים אינסופי , חשב את המקסימאלי המותר.

פתרון:
ראשית, נזהה את החתך הקריטי. נשים לב ש:

  • העומס הצירי והפיתול מתפלגים באופן אחיד לאורך החלק.
  • החתך בעל הקוטר הקטן מסוכן יותר.
  • אזור המעבר מקוטר קטן לקוטר גדול יוצר ריכוז מאמצים.

נסיק כי החתך הקריטי הוא האזור שבו הקוטר משתנה. מעתה נבחן רק את המאמצים המתפתחים בו.

לפי סיווג מאמצים תונדים, נחלק את העומסים לממוצעים והאמפליטודות:

ולכן המאמצים:

נחשב את מקדם ריכוז המאמצים הגאומטרי לפי MDN1_A15 טבלת מקדמי ריכוז מאמצים. כיוון ש- ו- ניתן לראות מהטבלאות ש:

לפלדה יש גם רגישות חריץ, כך שמהגרפים לרגישות חריץ אנו נסיק כי עבור :

ולכן מקדמי ריכוז המאמצים להתעייפות:

נוכל כעת לחשב את ההמאמצים השקולים לפי פון-מיזס (נשים לב שאין לנו כפיפה - bending):

כאשר בחישוב של מקדמי ריכוז המאמצים הם כי מדובר בחומר משיך.

עבור קריטריון גודמן, נותר לנו לחשב את (המתוקן לפי מארין). נזכור כי עבור פלדות ש- מתקיים ולכן:

  • מבחינת מקדם תיקון לגודל, מכיוון שהחלק נוצר בחריטה, לפי הטבלה , ולכן:
  • מבחינת מקדם תיקון לגודל, אין מאמצים אחידים וזהים בחתך (יש פיתול), כך ש- . כמו כן אנו במצב עמיסה מחזורית סובבת כי כלל הנקודות החומריות המצויות במרחק מציר הפיתול חווים את אותם המאמצים מבחינת מחזורית. לכן, נשתמש בנוסחה (SH6-20) ישירות:
  • כיוון שההעמסה מעורבת, נשתמש ב- .
  • אנו מניחים שאנו בטמפרטורת החדר ולכן .
  • דורשים אמינות, ולכן, לפי הטבלה, מקדם התיקון לאמינות הוא:
  • אין תופעות חריגות נתונות, ולכן .

נציב הכל במשוואת מארין כדי לקבל שסף ההתעייפות המתוקן הוא:

נציב בקריטריון גודמן עם מקדם הביטחון הנתון:

בבעיות התעייפות נהוג להשתמש בקריטריון לנגר כהערכה למקדם ביטחון לכניעה במחזור ראשון - אנו רוצים לוודא אנו נשארים בתחום האלסטי במחזור הראשון.
במקרה שלנו נציב את שקיבלנו בקריטריון:

סעיף ב’

עבור , מהו אורך החיים של החלק?

פתרון:
עבור ה- הנתון, נחשב את ו- מסעיף קודם:

כעת נוכל לחשב את המאמץ לתהליך מהופך לחלוטין :

נרצה לדעת אם אנחנו ב-LCF או HCF (או בכלל מעל סף ההתעייפות, למרות שתאכלס אנחנו יודעים שלא מכיוון שה- הנתון גדול משמעותית מה- שקיבלנו בסעיף קודם).
אנו יודעים מסעיף קודם ש-, כך שאנו מתחת לסף ההתעייפות. נמצא את (סף ההתעייפות ל- מחזורים) לפי שבר חוזק התעייפות. מהגרף, כיוון ש- , אנו יודעים ש- ולכן:

כיוון ש- קטן ממאמץ זה, נסיק שאנו ב-HCF, כך שנצטרך להשתמש במקדמים ו- הרלוונטיים ל-HCF בחישוב מספר המחזורים לכשל. לפי חוזק התעייפות ב-HCF:

נציב נתונים במשוואה האחרונה ונקבל:

הערה:

בחישוב של ו- השתמשנו ב- המתוקן.

עמודים המציינים את העמוד הזה