MDN1_009 בלמים ומצמדים

→ קודם: MDN1_008הבא: MDN1_010 ←

עקרונות יסוד

בפרק זה אנו נעסוק בקבוצה של מנגנונים המעבירים תנועה סיבובית בין שני אלמנטים.

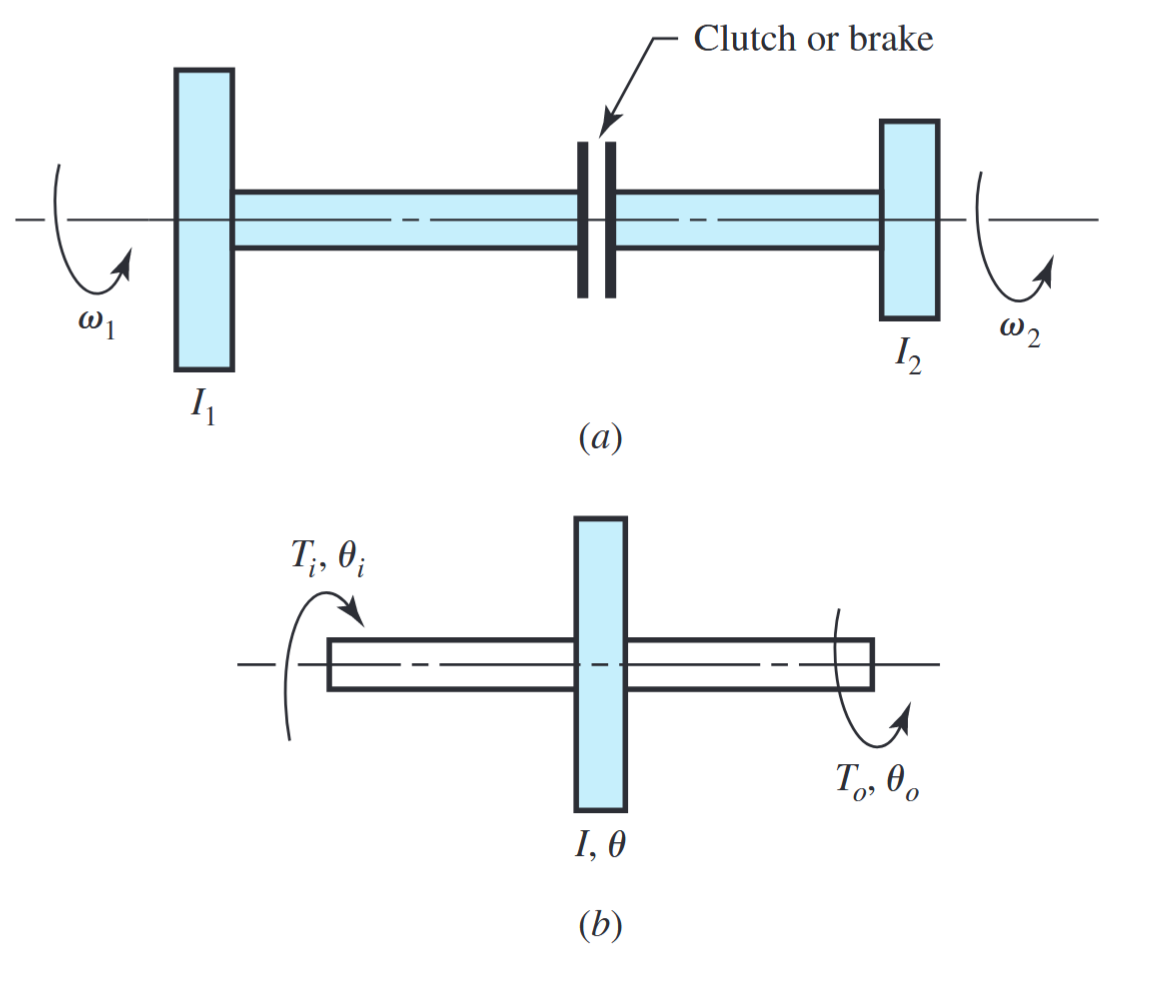
סכמה של (a) מצמד או בלם. (b) גלגל תנופה (flywheel). (Budynas et al., 2015).

בניתוח הביצועים של מצמד או מעצור אנו מעוניינים בגדלים הבאים:

• המומנט המועבר - transmitted torque.
• הכוח המפעיל - actuating force.
• הפסד האנרגיה - energy loss.
• עליית הטמפרטורה - temperature rise.

המומנט המועבר תלוי בכוח המפעיל, במקדם החיכוך ובגאומטרייה של המצמד. זוהי בעיה בסטטיקה שנדרש לפתור לגבי כל גאומטרייה שונה. בקורס אנו עוסקים בממסרות מפחיתות, ולכן המצמד יותקן בד”כ בציר הכניסה לתשלובת שם המומנט נמוך (אך המהירות הזוויתית גבוה).

ניתוח סטטי של מצמדים ובלמים

תהליך הניתוח של מצמד/בלם כללי מתואר כלהלן:

• נניח, נשער, או נמדוד את פילוג לחץ כלשהו בין משטחי החיכוך.
• נמצא את הקשר בין הלחץ הכי גדול והלחץ בכל נקודה.
• נמצא מתוך משוואות הסטטיקה את כוח הבלימה או המומנט, ואת התגובות בריתומים.

כאשר נדרש לתכנן מצמד, בדרך כלל מוגדר המומנט המועבר והמתכנן נדרש לבחור גאומטרייה, את רפידת הבילום ולחשב את הכוח המפעיל.\

ניקח לדוגמה את המקרה של המעצור דלת הבא:

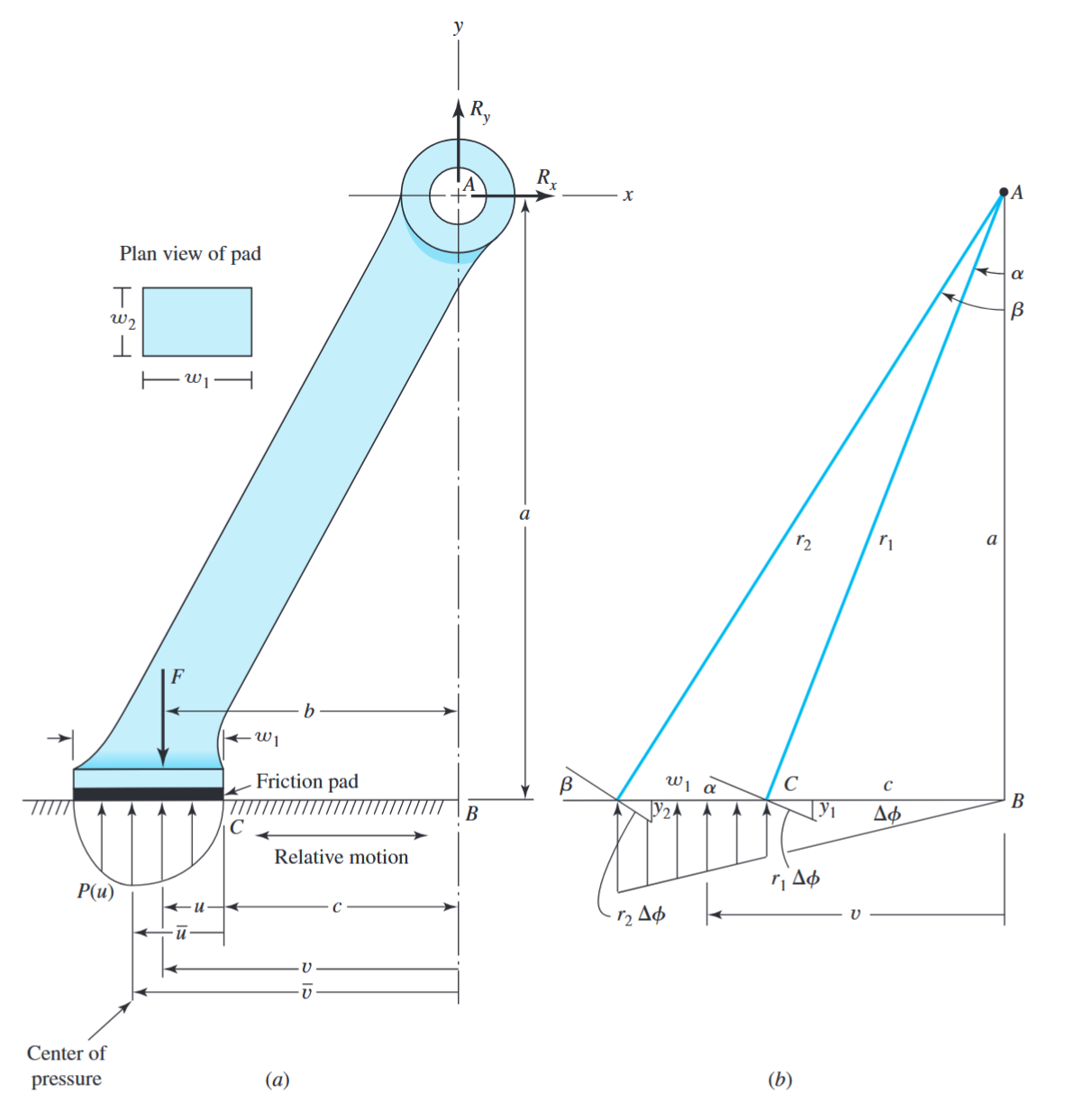
מעצור דלת טיפוסי. (Budynas et al., 2015).

עקב תנועת המשטח התחתון והכוח המפעיל מתקבלת מערכת הכוחות על הזרוע. נניח שהנעל די קצרה, ולכן הכוח המפעיל פועל באמצע הנעל. בנוסף, נוכל לומר, עבור נעל קצרה, שפילוג לחץ אחיד בין משטחי החיכוך.
לכן, קודת מרכז הלחץ של הנעל מקיימת (לפי האיור):

נסמן גם את הלחץ הממוצע ב- , כך שהכוח הנורמאלי הוא:

נבצע סכום מומנטים סביב הציר, בהנחה וגם הכוח מופעל באמצע הנעל:

בהנחה וידוע לנו הלחץ המקסימאלי המותר בחומר ממנו עשוי המצמד, הכוח המפעיל במקרה קיצון זה יהיה:

ניתן לראות כי הכוח המפעיל תלוי בגאומטרייה שנבחרה עבור המתקן. כלומר, הממדים ו- והשטח .

מצמדים ובלמים בעלי תוף פנימי

באיור הבא מתואר מצמד בעל תוף פנימי:

מצמד בעל תוף פנימי מופעל צנטריפוגלית. (Budynas et al., 2015).

כדי לנתח מנגנון בעל תוף פנימי, נפנה לגאומטרייהz שלו:

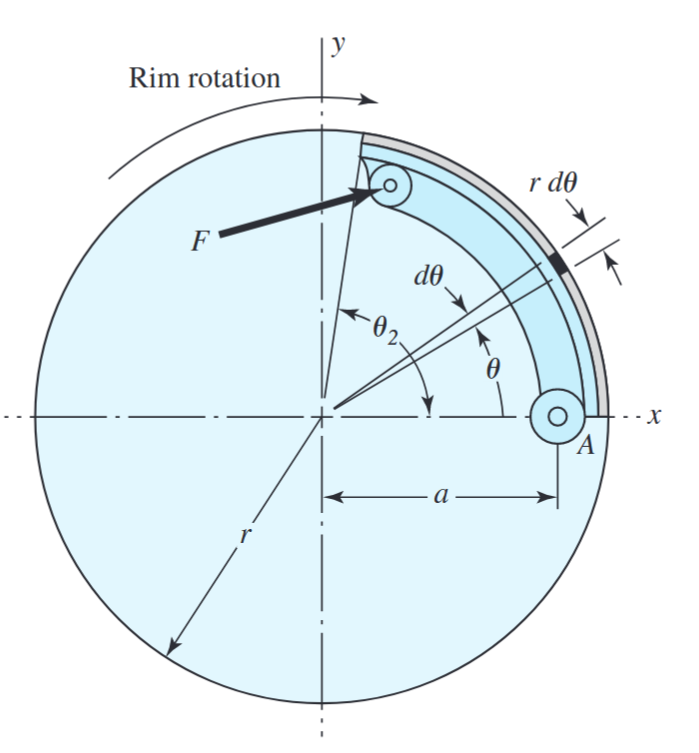
גאומטרייה של התוף הפנימי. (Budynas et al., 2015).

באיור לעיל אנו רואים נעל (משטח החיכוך) המתחילה בנקודה , שמופעל עליה כוח בצד השני שלה, . מאחר והנעל ארוכה, אנו לא יכולים להניח שפילוג הכוחות אחיד. התצורה המכנית הנתונה לא מאפשרת קיום לחץ בעקב הנעל (נקודה ), כך שנניח הלחץ בנקודה זו הוא אפסי.
נהוג להזניח את חומר החיכוך במרחק קצר מהעקב. ישנם תכנים בהם הפין סביבה הנעל מוחזקת יכול לזוז כדי לאפשר לחץ יותר גדול בעקב - מה שנקרא נעל צפה, ולא נעסוק במקרים אלו.

נניח ופועל לחץ על שטח דיפרנציאלי (תאכלס כפול עומק, אבל נניח רק את המקרה המישורי) של חומר החיכוך הנמצא בזווית מציר הפין, כפי שמוצג בציור לעיל. נסמן את הלחץ המקסימלי הממוקם בזווית מפין הציר. כדי למצוא את פילוג הלחץ על היקף הנעל הפנימית, נביט בנקודה באיור הבא:

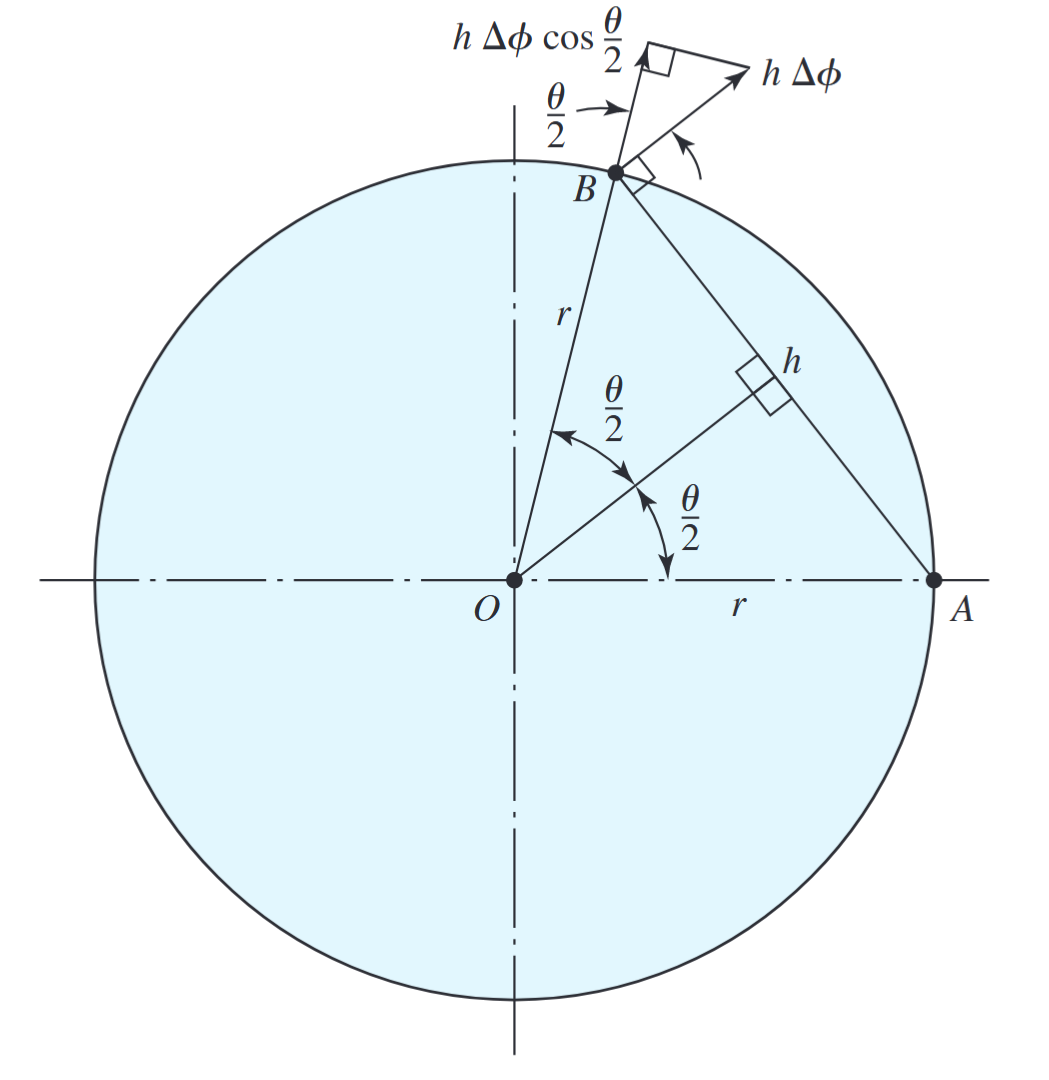
גאומטרייה של נקודה שרירותית על הנעל. (Budynas et al., 2015).

אם הנעל עוברת דפורמציה בזווית אינפיניטסימלית סביב הציר , הדפורמציה המקבילה ל- היא . מגאומטרייה על המשולש , מתקיים , כך ש:

הדפורמציה המקבילה לתוף היא ,שהיא:

לכן, הדפורמציה, ולפיכך הלחץ, פרופורציוני ל-. במונחים של לחץ בנקודה , בו הלחץ הוא מקסימלי:

לפילוג לחצים זה יש מאפיינים שימושיים:

• פילוג הלחץ סינוסואידי ביחס לזווית .
• אם הנעל קצרה, הלחץ הגבוה ביותר על הנעל הוא המתרחש בסוף הנעל, .
  
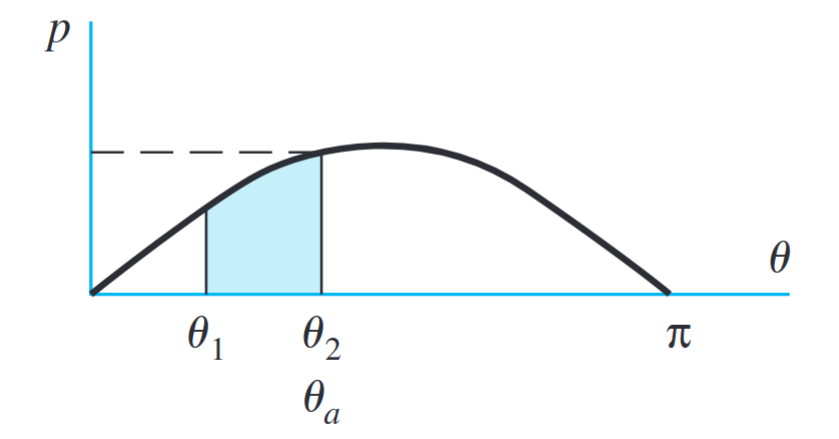
• אם הנעל ארוכה, הלחץ הגבוה ביותר על הנעל הוא , המתרחש ב- .
  

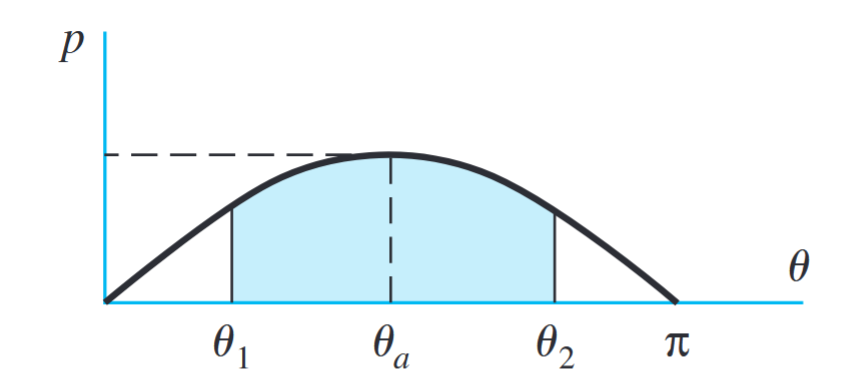
מאחר והמגבלות על חומרי חיכוך מבוטאים במונחים של לחץ מקסימלי מותר, אכפת לנו מהגודל , ולא מהאמפליטודה של הפילוג הסינוסואידי במשוואה (SH16-1). בלימה אופטימלית היא בלימה שמגיעה ללחץ המקסימלי לחומר.

כאשר , ניתן לראות מהמשוואה שהלחץ הוא אפס, כך שחומר החיכוך בעקב הנעל בקושי תורם לפעולת הבלימה, ונוכל להתעלם ממנו. תכן טוב ירכז כמה שיותר חומר חיכוך באזור הלחץ המקסימלי. תכן כזה מתואר בסכמה הבאה:

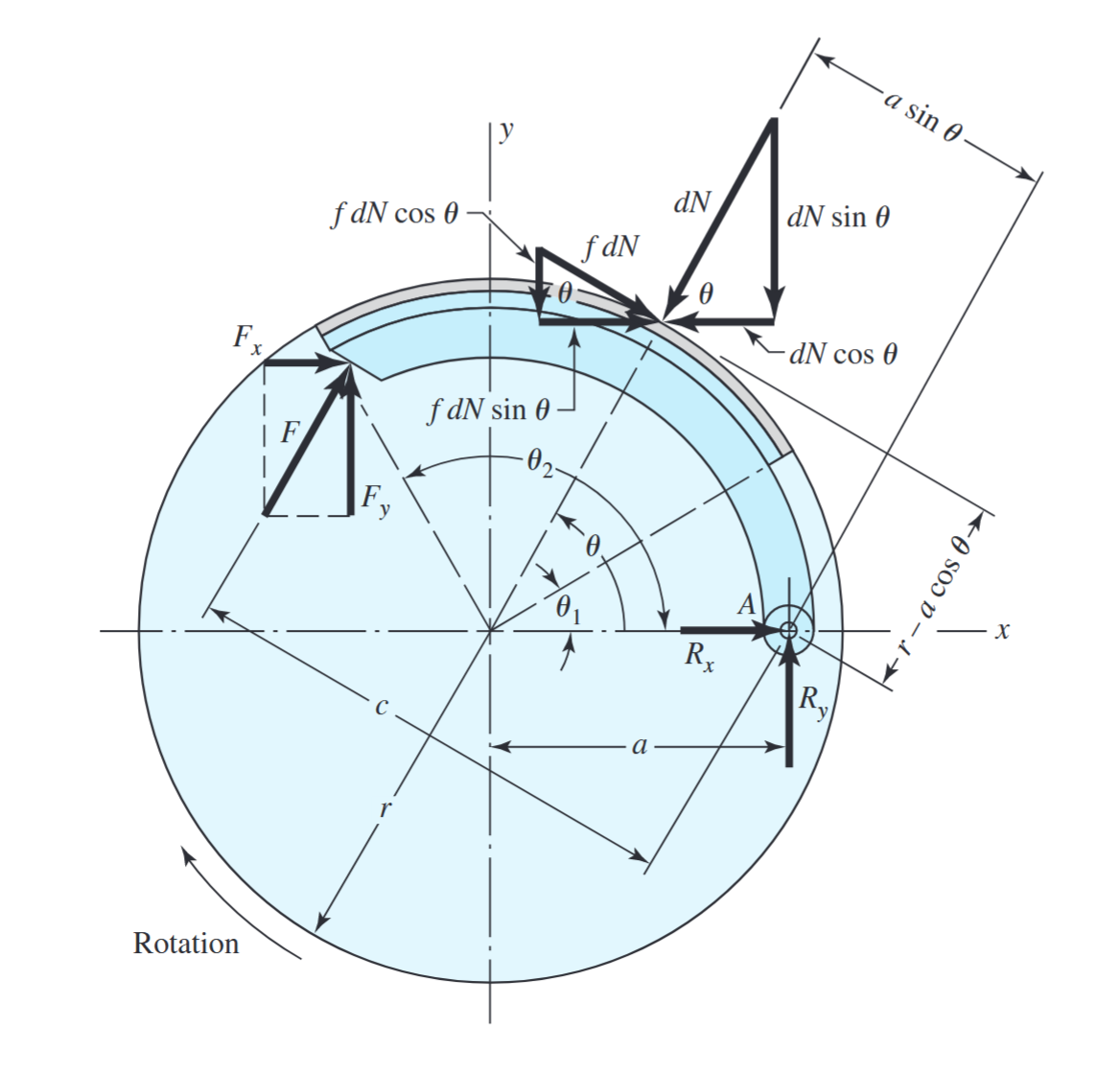
כוחות על הנעל. (Budynas et al., 2015).

באיור זה חומר החיכוך, הנקרא רפידה, מתחיל בזווית ביחס לציר בנקודה , ומסתיים בזווית . כל תצורה כזאת תניב פילוג די טוב של חומר החיכוך.

בבעיות תיכון לרוב דרוש איזשהו מומנט להעברה דרך המצמד. המתכנן נדרש לבחור את רפידת החיכוך ואת הגאומטרייה (), ואסור כמובן שהלחץ המקסימלי יעלה על הלחץ המותר לחומר (לפי טבלה 16-3). בנוסף, עליו לקחת בחשבון את הכוח המפעיל ואת הריאקציות בציר (בעקב).
כדי לחשב את הכוחות והעומסים במצמד או בלם, אנו מניחים את ההנחות הבאות:

1. הלחץ בכל נקודה על הנעל פרופורציונית למרחק מציר הנעל, כאשר היא אפסית על העקב.
2. השפעת הכוחות הצנטריפוגליים על הנעל מוזנחים. במקרה של בלם, הנעל לא סובבת, ולכן לא פועל עליה כוחות צנטריפוגליים. במצמדים, כן נצטרך לקחת את הכוחות הנ”ל בחשבון בתוך משוואות השיווי משקל.
3. הנעל היא קשיחה לחלוטין. מאחר ובעולם האמיתי זה לא המצב, נקבל פילוג לחצים שונה מהנחתנו.
4. מקדם החיכוך לא משתנה עם הלחץ, טמפרטורה, בלאי, או הסביבה.

נוכל להגדיר מספר קבועים לצורך פישוט המשוואות שנפגוש בהמשך:

מהסכמה לעיל, בכל זווית מציר הנעל פועל כוח נורמלי דיפרנציאלי שגודלו הוא:

כאשר הוא רוחב החומר החיכוך. נציב את ביטוי זה במשוואה (SH16-1) ונקבל:

משיווי משקל על המומנטים סביב הציר (העקב, לא הגלגל) נקבל שגודל המומנט כתוצאה מכוחות החיכוך הוא:

גודל המומנט סביב הציר (העקב, לא הגלגל) כתוצאה מהכוחות הנורמליים הוא:

הכוח המפעיל חייב לאזן בין שני מומנטים אלו, לכן:

נוכל לראות כעת שיש תנאי עבורו לא צריך כוח מפעיל כדי שהמערכת תינעל. שוב, אנו קוראים לתנאי זה נעילה עצמית, ועבור המקרה הנ”ל הוא מתרחש עבור . לכן, כדי שלא תיווצר נעילה עצמית, נרצה לבחור את כך ש:

נשים לב שאם כיוון הסיבוב משתנה אז גם כיוון פעולת כוח החיכוך משתנה ולכן:

המומנט הפועל על התוף ע”י נעל הבלימה הוא סכום של כוחות החיכוך ברדיוס התוף:

מבחינת הריאקציות בצירים, אם הסיבוב באיור לעיל הוא עם כיוון השעון, נקבל ש:

אם הסיבוב נגד כיוון השעון, הריאקציות הן:

נוכל גם לקשר בין הכוח המפעיל למומנט הבלימה המתקבל כתלות בזווית ע”י הצבת (SH16-6) ב-(SH16-4):

מצמדים ובלמים בעלי תוף חיצוני

המצמד-בלם המוצג באיור הבא הוא דוגמה למצמד המתכווץ ומופעל פְּנֵימָטִית (pneumatic):

מצמד בעל תוך חיצוני שמשולב ע”י צינור גמיש המתנפח עם לחץ אוויר. (Budynas et al., 2015).

בקורס לא נתעסק עם מצמדים מסוג זה, אבל חשוב לדעת שהם קיימים, ואת הלחצים, הכוחות, והמומנטים בהם ניתנים לפיתוח כמו בתוף פנימית.

מצמדי ובלמי סרט

באיור הבא מתואר סכמתית בולם סרט:

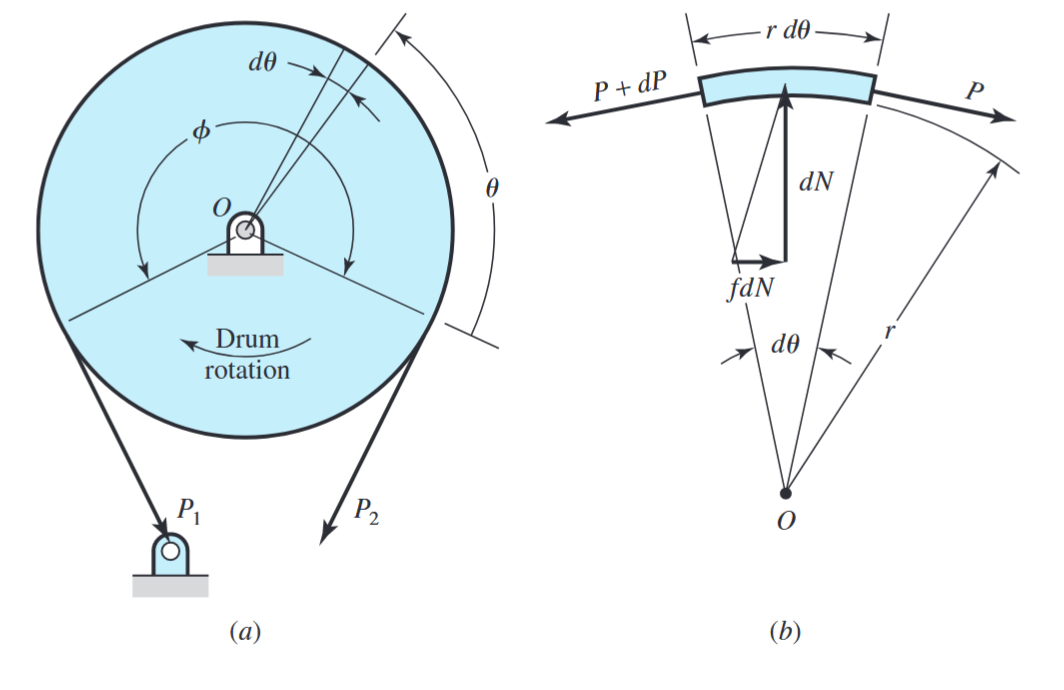
כוחות על בלם סרט. (Budynas et al., 2015).

הערה:

הסימון הוא עבור כוח מתיחה, בעוד הוא עדיין עבור לחץ. מאוד מבלבל. באסה.

עקב החיכוך וסיבוב התוף, הכוח המפעיל הינו קטן מהריאקציה בפין . מניתוח כוחות חיכוך וכוחות נורמליים דיפרנציאליים, אנו מקבלים מד”רים וביטויים דיפרנציאליים לכוחות ריאקציה שעליהם נוכל לבצע אינטגרציה כדי להסיק כי:
הקשר בין הכוחות לזוויות והחיכוך הוא

המומנט המועבר דרך הסרט נתון ע”י

הלחץ יחסית למתיחות בסרט:

ולכן הלחץ המקסימלי הוא:

מצמדים ובלמים ציריים

במצמד צירי מצעי החיכוך נעים בכיוון המקביל לגל. אחד מהמצמדים הראשונים מסוג זה הוא המצמד הקוני, אבל היום משתמשים יותר במצמדי דיסק. האיור הבא מתאר מצמד דיסק בפלטה-יחידה.

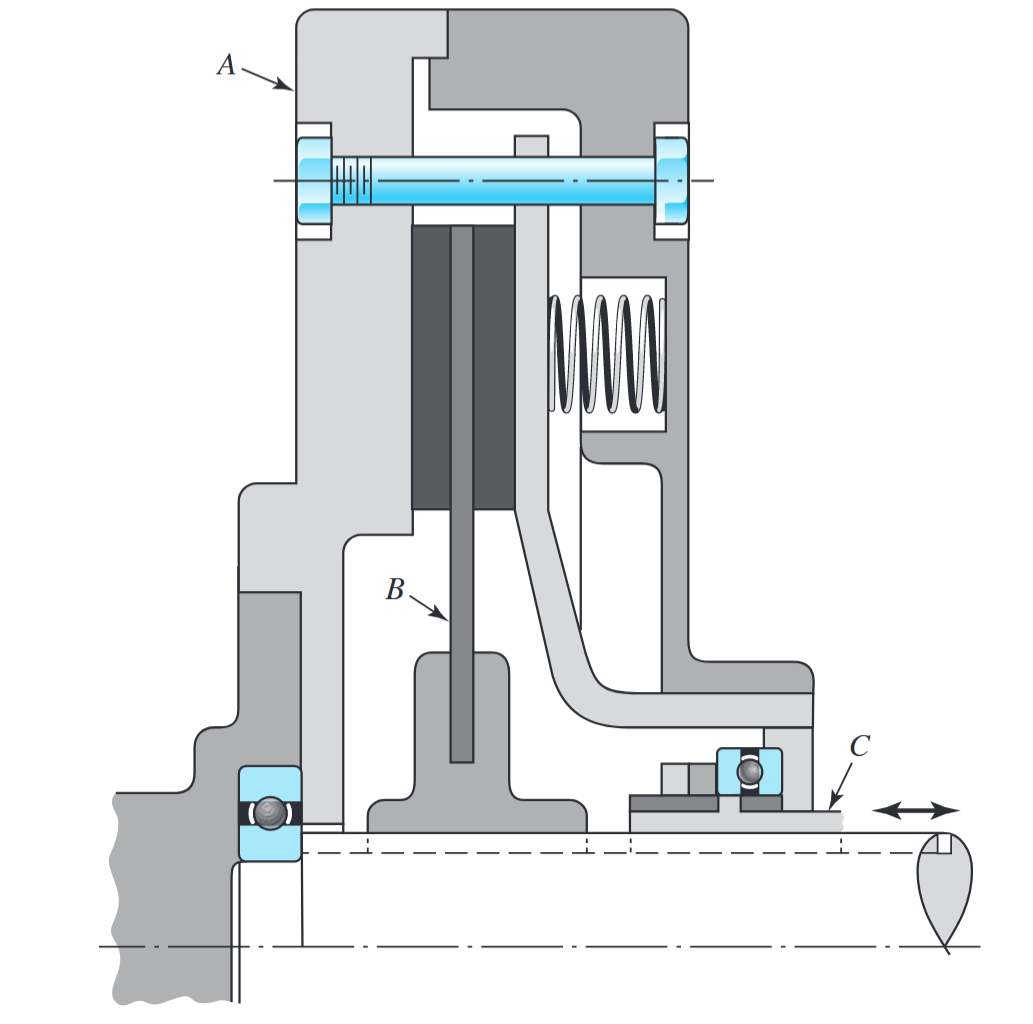
חתך על מצמד בפלטה-יחידה. הוא המניע; הוא הפלטה המונעת (מחוברת בשגם לגל המונע); הוא המפעיל. (Budynas et al., 2015).

בולם-מצמד רב-דיסקי מופעל-שמן. (Budynas et al., 2015).

נרצה כעת למצוא את היכולות של מצמד או בלם כזה במונחים גאומטריים וכתלות בחומר.

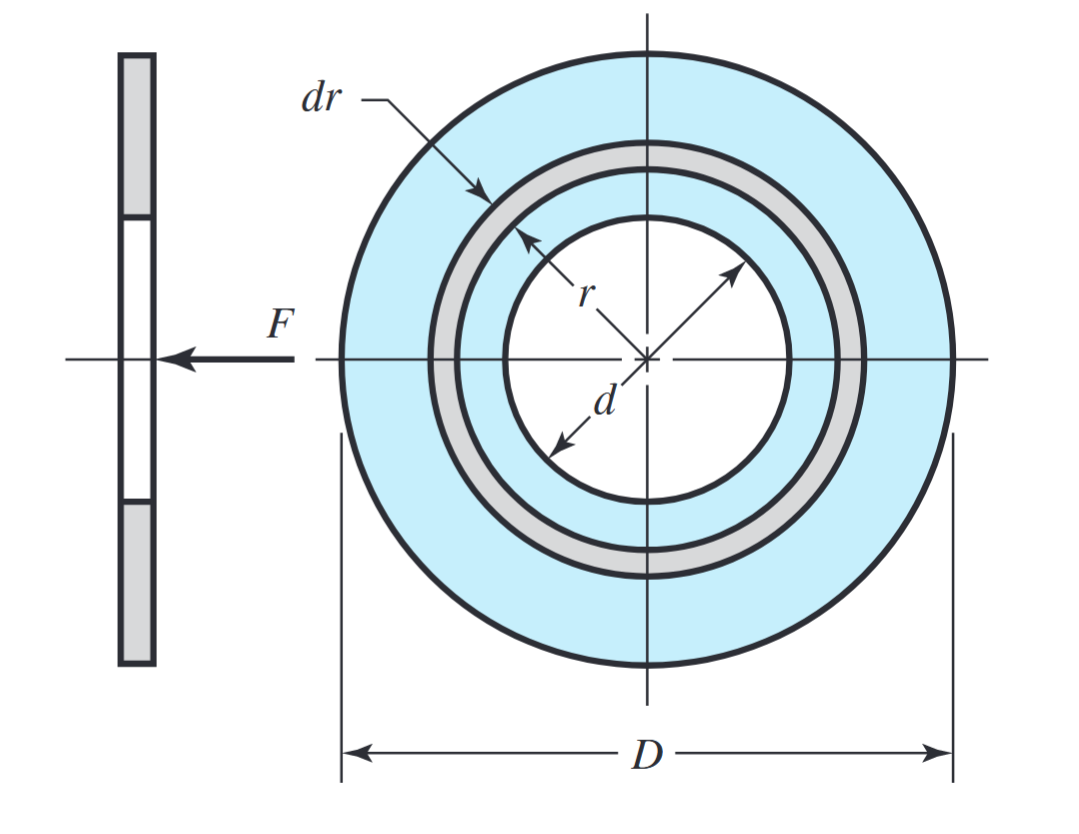
מצע דיסק חיכוך. (Budynas et al., 2015).

האיור לעיל מתאר דיסק חיכוך עליו פועל כוח צירי . נרצה לדעת מהו הדרוש ליצירת מומנט ולחץ כלשהו. ישנם שני דרכים לפתור את הבעיה זו, כתלות באופן בניית המצמד. אם הדיסק קשיח, אז הבלאי (wear) הכי עצים יתרחש קודם באזורים החיצוניים, כי עבודת החיכוך הכי גדולה שם. לאחר מספר מחזורים, רמה מסוימת של בלאי הצטברה על הדיסק, והפילוג לחצים על הדיסק ישתנה כך שהבלאי על הדיסק יישאר אחיד. זהו הבסיס לשיטה הראשונה לפתרון.
השיטה השנייה לבנייה כוללת קפיצים לקבלת פילוג לחצים אחיד לאורך שטח מסוים. מהנחה זו של פילוג הלחצים האחיד אנו מקבלים את השיטה השנייה לפתרון.

בלאי אחיד

לאחר שבלאי ראשוני התחיל להתרחש והדיסק הגיע לשלב בו ה-בלאי אחיד, ניתן לבטא את הבלאי כמותית ע”י:

כאשר נקרא מקדם שחיקה, הוא הלחץ, הוא המהירות המשיקית, ו- הוא זמן הפעולה.
הלחץ והמהירות יכולים להשתנות לאורך שטח הבלאי. לבלאי אחיד , מקבלים ש- אחיד. אם נסמן , ולפי גק”ש סובב, כאשר הוא המהירות הזוויתית, ניתן למצוא כי גם שטח הבלאי, הוא אחיד. הלחץ המקסימלי מתקבל איפה ש- מינימלי, , ולכן:

ניתן להראות מפיתוחים נוספים שהכוח המפעיל הוא:

הערה:

הצבנו במעבר הראשון. Shigley = Naknik.

המומנט שפועל על הדיסק:

ע”י הצבת (SH16-23) ב-(SH16-24) נקבל קשר יותר נוח בין שני הגדלים:

משוואה (SH16-25) נותנת את המומנט רק עבור משטח חיכוך יחיד, אז במידה ויש יותר, עלינו לכפול את בהתאם.

אם לא מדובר בדסקה מלאה, אלא בגזרה, כמו באיור הבא, עלינו להחליף במשוואות לעיל את באינטגרלים לעיל בעוד אינטגרציה:

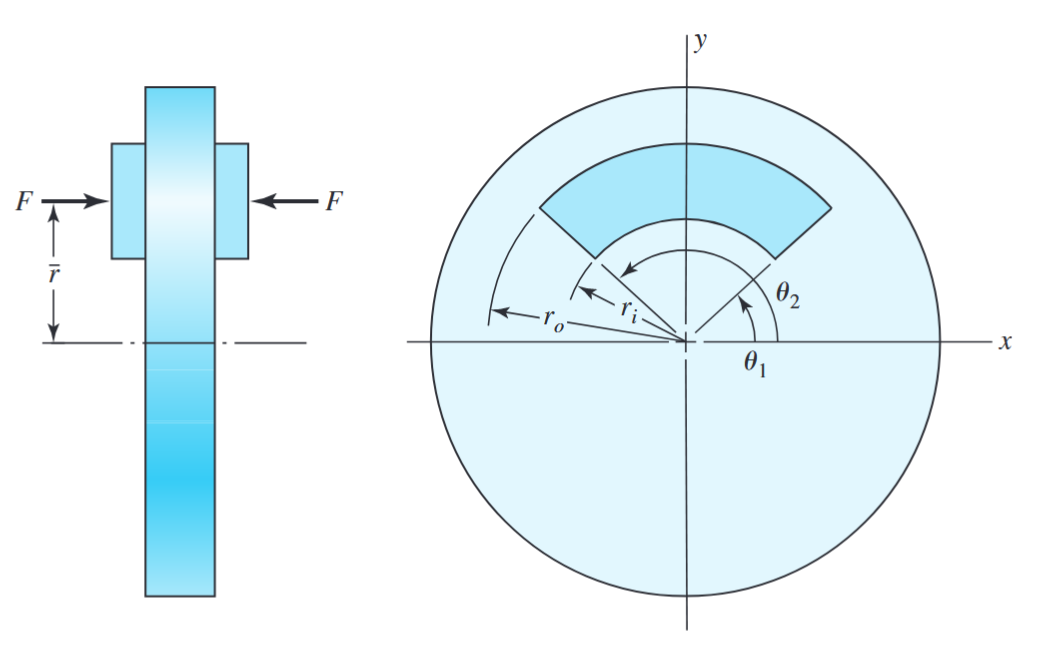
גאומטרייה של שטח מגע של גזרה טבעתית בבלם קליפר.

הכוח:

המומנט:

לחץ אחיד

כאשר אנו יכולים להניח לחץ אחיד על שטח הדיסק, הכוח המפעיל הוא פשוט המכפלה של הלחץ והשטח. זה נותן:

כמו מקודם, המומנט נמצא ע”י אינטגרציה של מכפלת כוח החיכוך והרדיוס:

ממשוואה (SH16-26) אנו יכולים לרשום את (SH16-27) כ:

נשים לב ששתי המשוואות (SH16-27) ו-(SH16-28) מחשבות את המומנט לזוג יחיד של מצעים במגע. אם יש יותר מזוג אחד של מצעים במגע, כלומר הבלם/מצמד הוא רב-דסקי, עלינו לכפול במספר המגעים את הערכים המתקבלים.

ממשוואות (SH16-25) ו-(SH16-28) נוכל לשרטט גרף של הגודל כתלות ביחס :

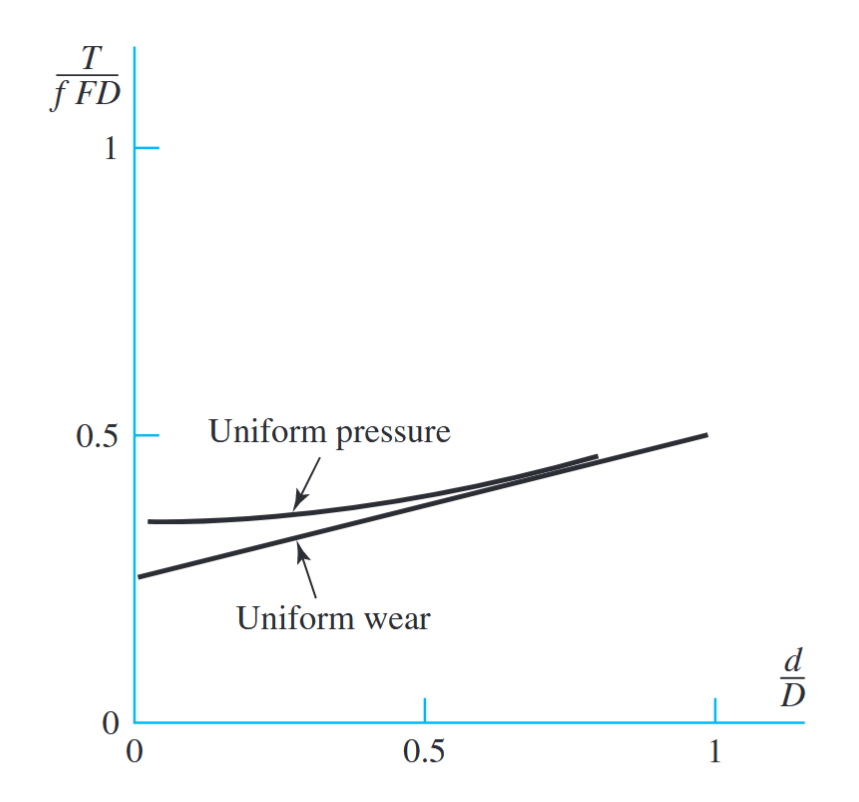
גרף חסר ממדי של הכוחות ביחס לאורכים בדסקות.

ניתן לראות מגרף זה שמצמד חדש (לחץ אחיד) תמיד יעביר יותר מומנט ממצמד ישן (בלאי אחיד). בנוסף, מאחר ורוב המצמדים מסוג זה מיוצרים ביחס של , ההבדלים הכי גדולים בין שני המצבים הם:

כך שהשגיאה ביניהם עומדת על . מכיוון שיש די הרבה אי וודאות לגבי מקדמי החיכוך האמיתיים, והוודאות בכך שמצמד חדשים מתיישנים עם הזמן, נעבוד לרוב רק עם משוואות בלאי אחיד.

אם מדובר בגזרה טבעתית, כמו בבלאי אחיד, עלינו להוסיף עוד אינטגרציה:

המומנט:

מצמדים ובלמים קוניים

האיור הבא מתאר סכמתית חתך של מצמד קוני, המכיל כוס המחוברת לגל, ו-קונוס הנע צירית על שגמים או סיומות משוננות, וקפיץ בורגי (helical spring) השומר על המצמד בשילוב.

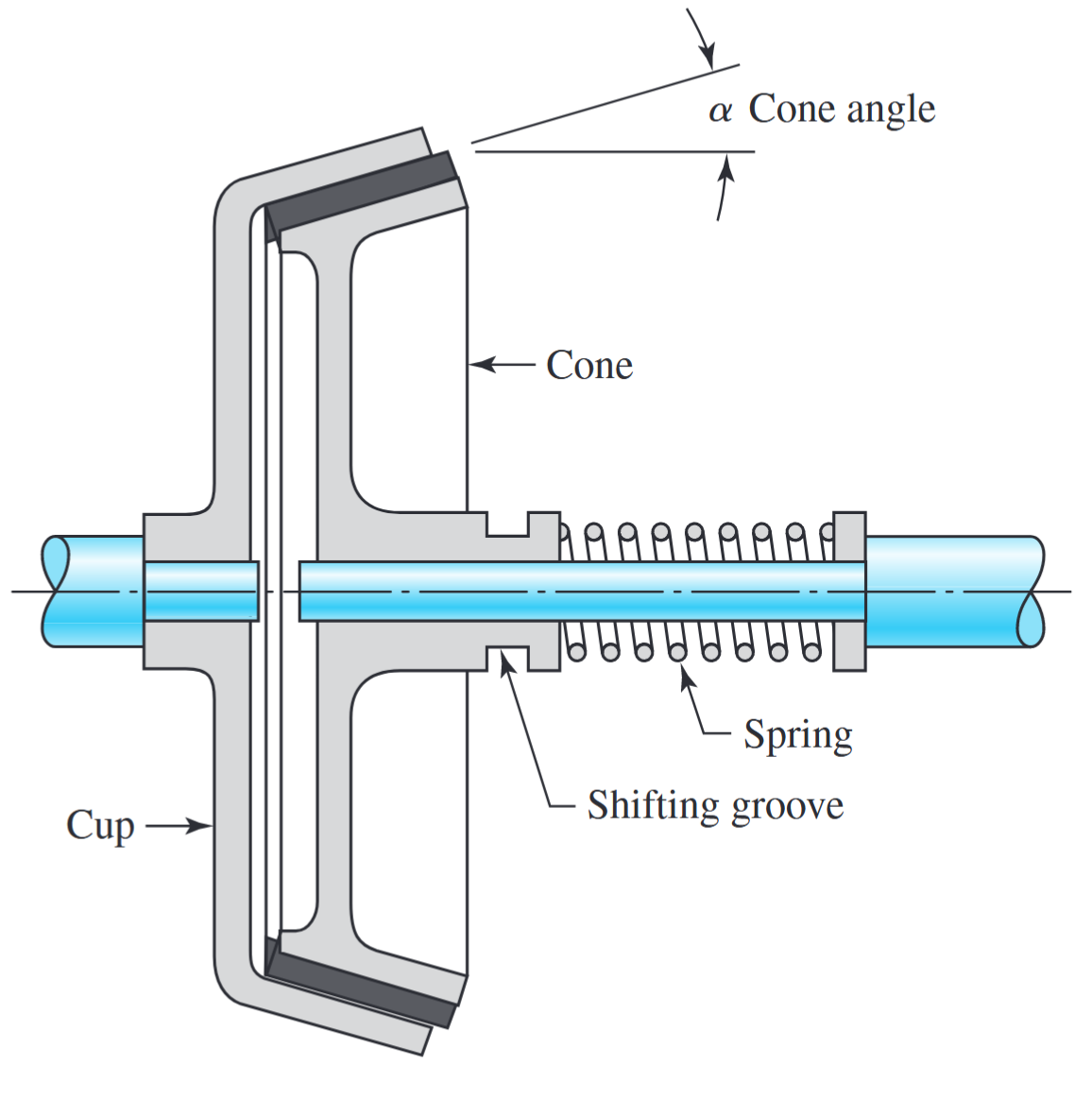
חתך של מצמד קוני. (Budynas et al., 2015).

המצמד יוצא משילוב ע”י תופסן (לא נראה באיור) שמתאים למגרעת (shifting groove) על קונוס החיכוך. זווית הקונוס , הקוטר, ורוחב הפנים של הקונוס הם הפרמטרים שאכפת לנו מהם בתכן. אם הזווית נמוכה מדי, למשל פחות מ-, אז הכוח הנדרש ליציאה משילוב של המצמד עלול להיות גבוה מדי. כתלות במקדמי החיכוך של החומרים, מקבלים איזון טוב בין החיכוך הרצוי לכוח יציאה משילוב עבור זוויות בין ל-.

כדי למצוא את הקשרים בין כוח ההפעלה והמומנט המועבר, נשרטט סכמתית את גאומטריית המצמד:

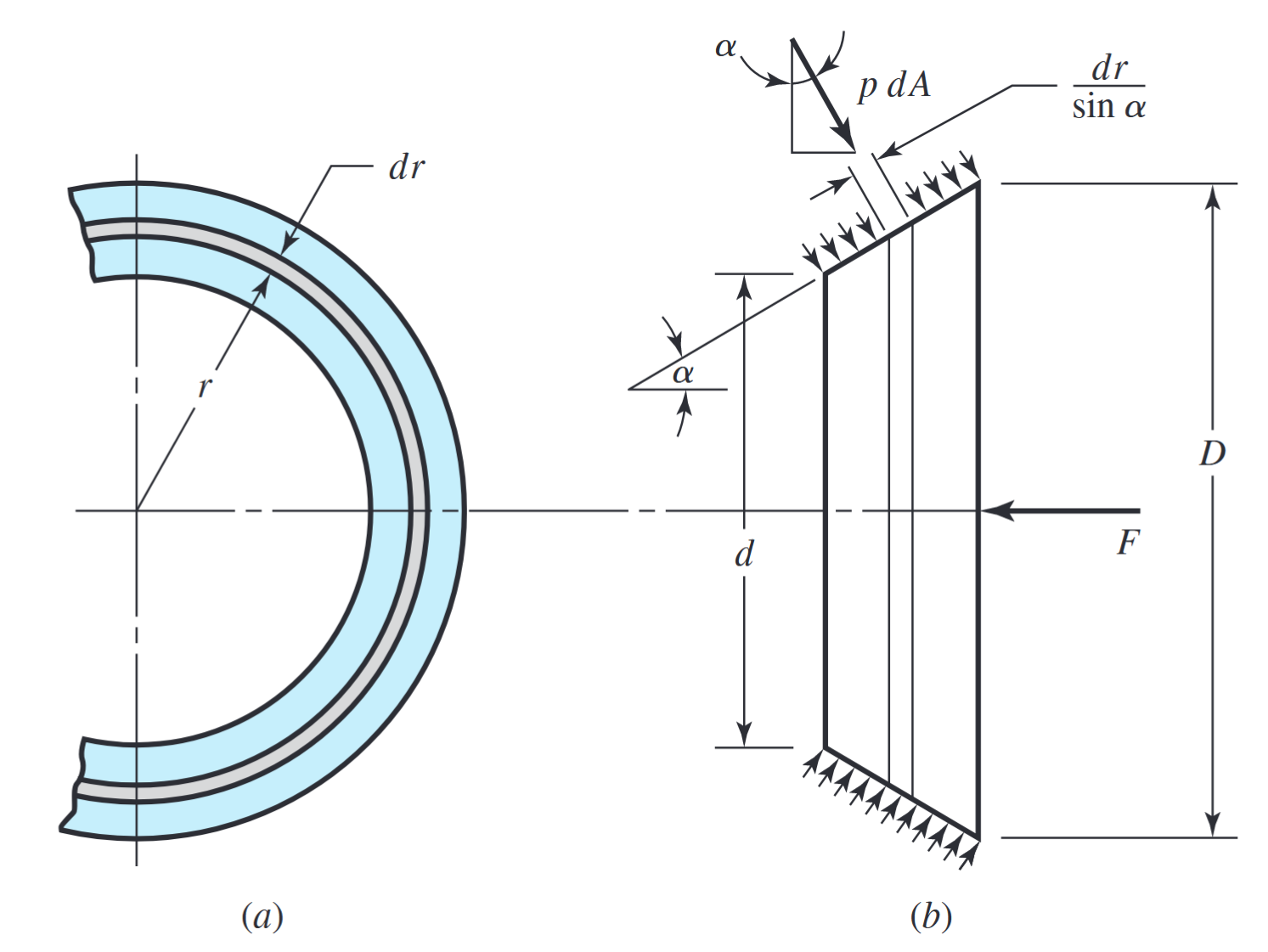
שטח מגע של מצמד קוני. (Budynas et al., 2015).

כמו במצמד צירי, נוכל לקבל את הקשרים להנחת בלאי אחיד, ואת הקשרים להנחת לחץ אחיד.

בלאי אחיד:
לבלאי אחיד, פילוג הלחצים יהיה אותו הדבר כמו במצמד צירי:

כעת, בעזרת האיור לעיל, ניתן להראות מאינטגרציה:

מבחינת המומנט:

נשים לב שמשוואה (SH16-24) היא מקרה מיוחד של (SH16-45) בו .
בעזרת (SH16-44) נוכל לרשום את (SH16-45) לפי:

לחץ אחיד:
בהנחה והלחץ אחיד, , נקבל שהכוח המפעיל הוא:

המומנט הוא:

בעזרת שתי משוואות אלו ניתן למצוא כי:

שיקולי אנרגיה

בתהליך הבלימה או ההצמדה קיימת החלקה במשטחי החיכוך. החלקה זו גורמת להפסדי אנרגיה המתבטאת בהתחממות.
נוכל לבטא את התחממות זו בעזרת שיקולי אנרגיה. אנו יודעים ממאזן תנע זוויתי, ולפי האיור בעקרונות יסוד:

מאינטגרציה:

כאשר ו- הן המהירויות הזוויתיות ההתחלתיות של האינרציות ו- בהתאמה.
ההפרש בין מהירויות אלו, שנקרא גם המהירות היחסית, יהיה פשוט:

פעולת ההצמדה מופסקת ברגע ששתי המהירויות ו- מושוות. נסמן את רגע זה ב-, ונקבל מ-(SH16-50) שהוא:

משוואה זו מראה שהזמן הדרוש לפעולת השילוב פרופורציוני להפרש המהירויות, ופרופורציוני הפוך למומנט.
הנחנו בכל חישוב זה שהמומנט הוא קבוע, אז נוכל ממשוואה (SH16-50) למצוא את קצב דיסיפציית האנרגיה לאורך פעולת ההצמדה:

מה שמראה שקצב הדיסיפציה הכי גדול בהתחלה, .
סך דיסיפציית האנרגיה לאורך פעולת ההצמדה היא פשוט אינטגרל על גודל זה:

נשים לב שסך האנרגיה פרופורציוני להפרש המהירויות בריבוע ואינה תלויה כלל במומנט.

עליית הטמפרטורה נתונה ע”י:

כאשר הוא המסה של המצמד ב-, ו- הוא קיבול החום הסגולי. נשתמש ב- לפלדות וברזל יצוק.

תרגילים

תרגיל 1

נתון בלם בעל שתי רפידות פנימיות. קוטר התוף הוא . נתונות הזוויות:

הזווית בין שתי הרפידות הוא , כך שלמעשה, הבלם סימטרי. המרחק הרדיאלי לנקודות הצירים הינו . רוחב הרפידה הוא , והנתונים על רפידת הבלימה הם:

סעיף א’

מתאן את הכוח שיש להפעיל על מנת לנצל את מערכת הבלימה בצורה האופטימלית (הכוח המפעיל, ).

פתרון:
הפעלה אופטימלית מתרחשת במקרה בו הלחץ ברפידה הימנית מגיע ל-, עבורו הכוח מחושב באופן הבא:

נמצא את המרחקים הגאומטריים:

נציב נתונים ונקבל:

מכיוון ש- , זווית הלחץ המקסימלית תהיה . נחשב את המומנטים סביב הציר שיוצרים הכוח הנורמלי וכוח החיכוך:

נציב ביטויים אלו בביטוי לכוח ונקבל:

סעיף ב’

מהו הלחץ המקסימלי בנעל השמאלית ()?

פתרון:
מבחינת הלחץ המקסימלי על הנעל על השמאלית, ניתן להראות כי הקשר בין (הלחץ המקסימלי על הנעל הימנית) לבין (הלחץ המקסימלי על הנעל השמאלית) הינו:

נציב נתונים ונקבל:

סעיף ג’

מהו סך כל מומנט הבלימה שמופעל על התוף ?

פתרון:
סך מומנט הבלימה נתון ע”י:

לפי הנוסחה ל-:

נקבל:

סעיף ד’

מצאו את גודל הריאקציות בצירים.

פתרון:
נחשב תחילה את האינטגרלים:

לכן הריאקציות עבור רפידה (1):

לכן גודל הריאקציה:

באותו אופן ניתן לחשב עבור .

תרגיל 2

נתון בלם סרט כמתואר באיור, בעל הנתונים הבאים:

• רוחב הרפידה , עם וגם .
• קוטר הגלגל הינו .
• המרחק בין מרכז הגלגל לנקודת קשירת החבל הינו .

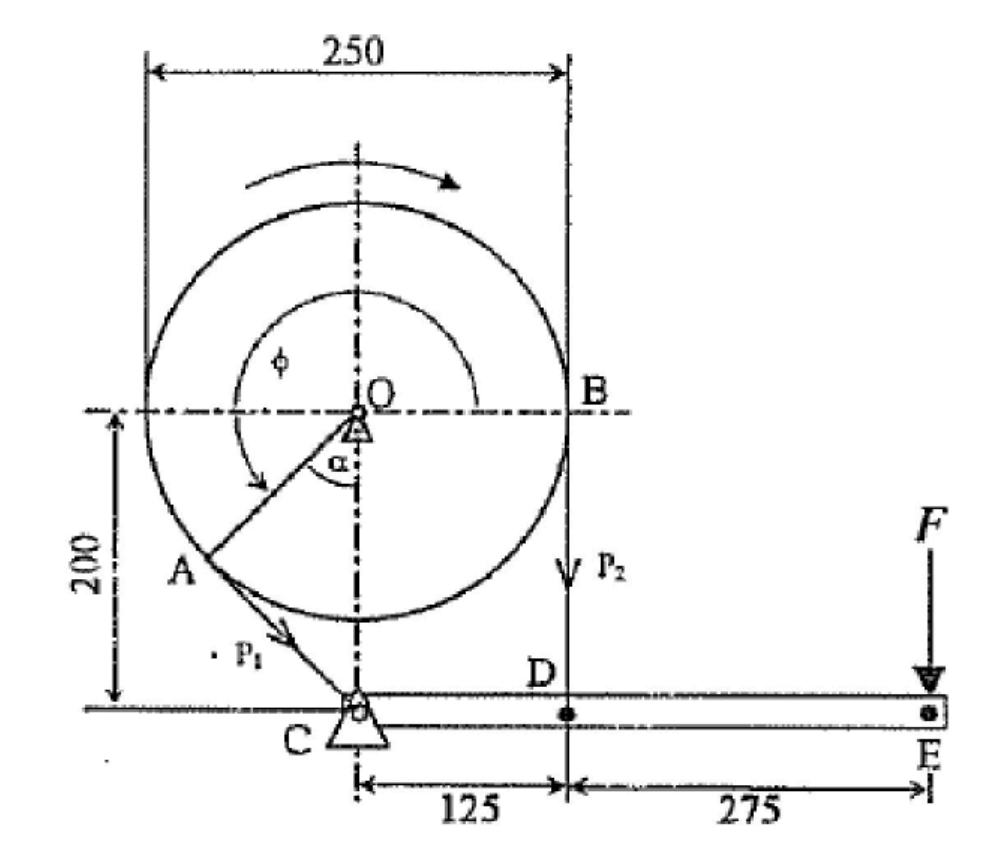
סכמת הבלם סרט.

סעיף א’

בהנחה כי הבלם מתוכנן ללחץ מקסימלי ברפידה, חשב את המומנט המקסימלי.

פתרון:
מומנט הבלימה במצב של סיבוב עם כיוון השעון מחושב לפי:

מאחר ו- (לפי (SH16-19)):

בנוסף, לפי (SH16-22), ניתן למצוא כי:

כדי למצוא את , נמצא קודם את מגאומטרייה:

לכן זווית הליפוף היא:

נוכל להציב בחזרה לביטוי ל-, ונקבל:

סעיף ב’

חשב את הכוח הדרוש לקבלת המומנט המקסימלי.

פתרון:
הכוח המירבי המותר הינו הכוח אשר יוצר לחץ בנקודה . על מנת ליצור מצב כזה, מתיחת הקצה החופשי תתוכנן באמצעות הקשר שחושב:

על מנת למצוא את הכוח , נבצע מאזן מומנטים עבור הקורה סביב הנקודה :

לכן:

תרגיל 3

נתון בלם דיסק שתוכנן לבלאי אחיד. הדיסק בעל קוטר חיצוני של וקוטר פנימי של . הבלם בעל מקדם חיכוך של ולחץ מקסימלי של . נדרש לחשב את מומנט הבלימה והכוח הדרוש באם נתון כי הבלם הינו בעל רפידה כפולה בצורת גזרה של .

פתרון:
לפי משוואה (SH16-34), מאחר ובמקרה שלנו המעגל לא מלא, ויש שתי רפידות:

נשים לב שבמקרה שלנו, וגם . לכן:

מבחינת הכוח:

הערה:

אני חולק כאן על הפתרון שמופיע במודל, שמה הם אמרו:

אבל בספר רשום במפורש שאת צריך להכפיל במספר הרפידות, בעוד את לא צריך.

תרגיל 4

נתון גלגל תנופה במשאל עם עובי וקוטר של המסתובב במהירות של . על מנת להביאו לעצירה מוחלטת, מופעל כוח על בלם דסקאות מסוג בלאי אחיד. לבלם דסקאות פלדה בקוטר חיצוני של וקוטר פנימי אופטימלי, כאשר לכל דסקה יש רפידות משני הצדדים. בנוסף, הרפידות עשויות מעור טבול בשמן בעל הנתונים ו-.

סעיף א’

כמה זמן ייקח לגלגל התנופה לעצור?

פתרון:
נחשב את מומנט האינרציה של הגלגל:

נציב נתונים ונקבל:

המומנט בלימה עבור רפידה בודדת (עבור בלאי אחיד) הינו:

מאחר ויש שלוש דסקאות פלדה, כל אחת מהן בעלת שתי רפידות, נסיק כי סך המומנט הוא:

הזמן לעצירה:

במקרה שלנו, וגם , ולכן:

נתון כי . נציב ביחד עם שאר הנתונים ונקבל:

סעיף ב’

האם הבלם מנוצל בצורה מיטבית?

פתרון:
הקשר בין מומנט הבלימה ללחץ הרפידה הינו:

לכן הלחץ המקסימלי המופעל הינו:

מאחר ו- , נסיק כי הבלם אינו מנוצל בצורה המיטבית.

→ קודם: MDN1_008הבא: MDN1_010 ←