PHY1_005 עבודה ואנרגיה

→ קודם: PHY1_004הבא: PHY1_006 ←

עבודה ואנרגיה

חוקי ניוטון מאפשרים לנתח הרבה סוגי תנועה. הבעיה היא שלעיתים השימוש בהם מסובך ודורש פרטים שאין ברשותנו. הנה דוגמה:
דיסקית נשלחת על דרך עקלקלה ללא חיכוך. הדרך כוללת עליות וירידות בצורות ובזוויות שונות. המהירות ההתחלתית של הדיסקית היא וגובהה ההתחלתי הוא מטר. בעזרת חוקי ניוטון, האם אפשר לחשב את מהירות הדיסקית כשהיא מגיעה לסוף המסלול בגובה מטר?
התשובה היא שכן, אך נצטרך לדעת את הפרטים על צורת המסלול לאורך כל הדרך. גם אם נדע פרטים אלה, החישוב עלול להיות מורכב.

במאה ה-19 מדענים ומהנדסים הבינו שיש דרך אחרת, לפעמים יותר חזקה, כדי לחשב תנועה. השיטה הזאת היא כללית, ואפשר להכליל אותה למקרים מעבר למכניקה כמו אינטראקציות כימיות ופונקציות ביולוגיות. שיטה זאת היא אנרגיה, עליה נדבר בהרחבה בשני השיעורים הבאים. אנרגיה היא מספר שאנו משייכים למערכת של גוף אחד או יותר. אם כוח משנה את מצב אחד או יותר מהגופים, לדוגמה על ידי הזזתו, אז המספר הזה משתנה. אחרי ניסוים אינספור, מדענים ומהנדסים הבינו דרך להגדיר מספר זה כדי לנבא תוצאות של תהליכים מורכבים (כמו תנועת הדיסקית) בקלות.

עבודה חד-ממדית

נתחיל בלהגדיר גודל קשור חשוב הנקרא עבודה במקרה החד ממדי.

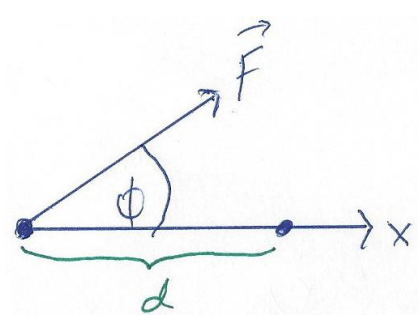
העבודה שכוח עושה כשהוא מזיז גוף מנקודה לנקודה הוא:

הגדרה:

כאשר הגדרנו את ציר התנועה כציר ה-.

דוגמאות:

1. כוח קבוע הפועל על גוף לאורך ציר מ- ל-. במקרה זה:

דוגמא פרטית זו נותנת את האינטואיציה מאחורי מושג העבודה. העבודה לוקחת בחשבון גם את הכוח וגם את הדרך שעבר הגוף בצורה של כוח כפול דרך. באופן אינטואיטיבי אנו מרגישים שאם כוח נתון פעל לאורך דרך ארוכה יותר, השפעתו על הגוף תהיה גדולה יותר.
2. הכוח שמפעיל קפיץ על מסה תלוי עד כמה הקפיץ מכווץ או מתוח. כלומר הכוח משתנה עם מקום המסה. מכאן שהעבודה שעושה הקפיץ על מסה הנעה מנקודה לנקודה היא:

עבודה היא סקלר. ערכה יכולה להיות מספר חיובי, שלילי או אפס. אם הכוח הוא בכיוון מנוגד לתנועה, כמו בדוגמא שפתרנו, אז העבודה שעושה הכוח היא שלילית. אם באותו כיוון אז חיובי.

יחידות הכוח הם הנקרא ג’ול. כשמדברים על עבודה, צריך להגדיר עבודה של איזה כוח. העבודה הכוללת היא סכום העבודות מכל הכוחות.

משפט העבודה-אנרגיה

בעזרת החוק השני של ניוטון (בהנחה שהמסה קבועה) והביטוי עבור :

נמצא ביטוי חשוב עבור העבודה שעשה שקול הכוחות:

חשוב להדגיש שמכיוון שהשתמשנו בחוק השני של ניוטון, ביטוי זה נכון עבור העבודה שעשה שקול הכוחות.

אנו קוראים לגודל האנרגיה הקינטית. זוהי האנרגיה הקשורה בכך שלגוף יש מהירות. מכאן שהעבודה הנעשית כששקול הכוחות פועל על גוף הנע בין A ל B היא:

משפט:

ביטוי זה נקרא משפט העבודה-אנרגיה. במילים היא אומרת שהעבודה של הכוח השקול שווה לשינוי באנרגיה הקינטית של הגוף. אם העבודה היא חיובית אז האנרגיה הקינטית גדלה במעבר מ- ל- ואם העבודה שלילית האנרגיה הקינטית קטנה. עבור עבודה אין שינוי באנרגיה הקינטית. באופן אינטואיטיבי, העבודה מסכמת את פעולתו של רכיב הכוח לאורך כיוון התנועה. רכיב זה גורם לשינוי המהירות.

עבודה בתלת ממד

כעת נדמיין גוף הנע בתלת ממד מנקודה לנקודה . באופן כללי, הכוח יכול להצביע לא רק לאורך מסלול התנועה:

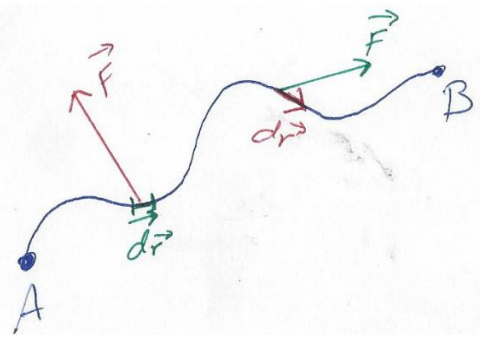
נפרק את הכוח לאורך הצירים:

ההעתק האינפיטסימלי הוא:

כלומר ההעתק האינפיניטסימלי התלת ממדי הוא הסכום הוקטורי של ההעתקים האינפיניטסימליים בכל אחד מהצירים. נגדיר שהעבודה שהכוח עושה כשהוא פועל על הגוף לאורך ההעתק האינפיניטסימלי הוא:

אם נסכום את כל ההעתקים האינפיטסימליים לאורך מסלול, נקבל את כלל העבודה שהתבצעה במסלול זה. סכימה זו של ערכים אינפיטסימליים היא אינטגרל:

ולכן נוכל לומר כי:

הגדרה:

ביטוי מתמטי מסוג זה נקרא אינטגרל קווי. הוא סוכם את מכפלת הטלת הכוח על העתק האינפיניטסימלי לאורך המסלול מ- ל-.

דוגמאות:

1. נדמיין גוף, לדוגמא חרוז, הנע לאורך חוט מתוח לאורך ציר x ללא חיכוך. כוח קבוע הפועל בזווית לחוט, מאיץ אותו.
   
   רכיב הכוח הפועל לאורך הדרך שעבר החרוז (היטל הכוח על ציר ) הוא:

מכיוון שהחרוז נע לאורך ציר x בלבד, ההעתק האינפינטיסימלי הוא .
נחשב את העבודה שעשה הכוח:

אנו רואים שרק רכיב הכוח בכיוון תנועת הגוף משפיע על העבודה. באופן אינטואיטיבי אנו מעוניינים רק ברכיב הכוח בכיוון התנועה מכיוון שזהו הרכיב שישנה את האנרגיה הקינטית של הגוף. באופן מתמטי ההיטל של הכוח על כיוון תנועת הגוף נעשה על ידי המכפלה הסקלרית .

הערות:

1. שימו לב שאנו לא מדברים על המושג היום יומי של עבודה שמשמעותו כל מטלה פיסית או מנטלית. לדוגמא, אם דוחפים קיר, מתעייפים כי השרירים נתפסים. בשפת היום יום זוהי עבודה קשה, אך אין זו עבודה לפי ההגדרה בפיסיקה.

קשר בין עבודה, כוח ומהירות

נשתמש בקשר:

נציב בהגדרה של עבודה:

כאשר גבולות האינטגרציה הם כעת עבור משתנה הזמן. הוא הרגע בו הגוף נמצא בנקודה וכך גם עבור ו-.

דוגמאות:

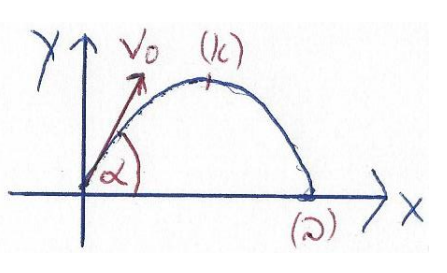
1. גוף בעל מסה נזרק בזווית מעל האופק, במהירות .
   

• חשבו את עבודת כוח הכובד על הגוף עד להגעתו לשיא הגובה.
  פתרון:
  אנו רוצים לחשב את הגודל .
  אנו יודעים ש:

בבעיה זו הזווית בין ל- משתנה מנקודה לנקודה. זה יקשה על חישוב . מכאן שהכי נוח להשתמש בביטוי הקרטזי. מכאן ש:

כוח הכובד פועל נגד כיוון הציר האנכי () ולכן העבודה היא:

זרקנו מ-, כל מה שנותר הוא לחשב את .
מתנועה בליסטית אנו יודעים כי:

נציב עבור הביטוי של העבודה:

מכיוון שהכוח פועל נגד כיוון התנועה, העבודה היא שלילית.

• חשבו את עבודת כוח הכובד על הגוף עד להגעתו לגובה הזריקה.
  פתרון:
  בהגעתו לגובה הזריקה הכוונה ל-. לכן:

כלומר, לא מתבצעת עבודה. העבודה שכוח הכבידה עשתה כשהגוף עלה הייתה שווה בגודלה והפוכה בסיומה מהעבודה בדרך למטה.

→ קודם: PHY1_004הבא: PHY1_006 ←