פנגייה

SLD2_002 מישורים ראשיים

• זמן קריאה: 8 דק'

מאמצים מישוריים

נאמר כי חומר נמצא תחת מאמץ מישורי אם הוא לא נמצא תחת מאמץ באחד מן הצירים. במקרה זה, הטנזור יראה כך:

סיבוב טנזור בדו-ממד

במקרה של מאמץ מישורי, נביט בסביבת נקודה (אינפיטסימלית) בחומר:

משיווי משקל על הדג”ח, נסיק כי (לפי צירי ו-):

באותו אופן נבצע שיווי משקל על ציר ונגיע לביטוי:

נציב בשני הביטויים ל- ו- את הזהויות:

ונקבל:

נוסחאות מגעילות אבל הן מראות לנו שאם אנו יודעים את רכיבי המאמצים () בשני כיוונים ניצבים בנקודה מסויימת, אז ניתן לחשב את רכיבי המאמצים בנקודה זו בכל כיוון (כפונקציה של ).

הערה:

בהמשך נפגוש עוד טנזורים חוץ מטנזור המאמץ, שעבורם נרצה לבצע “סיבוב”. נוסחאות אלו תקפות גם אליהם. למשל, עבור טנזור העיבור (שהוא גם סימטרי) שנפגוש בהמשך:

מאמץ נורמלי מקסימלי בדו ממד

לפעמים נרצה גם למצוא את ערכי המאמצים המקסימליים - . נוכל לגזור את הביטוי ל-, ולהשוותו לאפס:

קיבלנו כי קיימים שתי זוויות עבורן מקסימלי, ששתיהן ניצבות אחת לשנייה. לערכי בזוויות אלו אנו קוראים מאמצים ראשיים.

נוכל להציב את הערכים של לביטוי שקיבלנו מקודם ל-, ובכך לקבל שני ערכים, ו-. אין לי כוח להראות את ההוכחה המתמטית למה שנקבל, אז הנה לינק לויקיפדיה שמראה את זה. נקבל כי:

(נסמן תמיד ש- הוא הגדול יותר מ-).

book

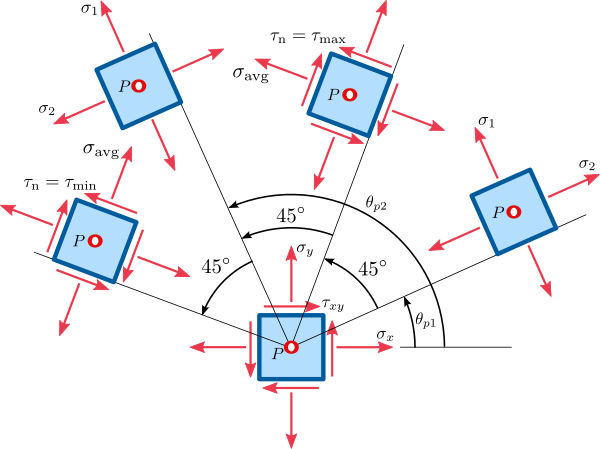
מצב המאמצים בדו ממד, כל פעם בזווית אחרת כדי להמחיש את המאמצים המקסימליים והמינימליים.

הערה:

בהמשך נפגוש עוד טנזורים שנרצה למצוא את הערכים המקסימליים שלהם. עבור טנזור העיבור (שהוא גם טנזור סימטרי):

מאמצי גזירה מקסימליים בדו ממד

כאשר , החומר האינפיטסמלי (הריבוע) מסובב בכיוון של המאמצים הראשיים, ולכן הטנזור שלנו ייראה כך:

מהביטויים ל- ו- הכלליים, נוכל לפשט אותם למקרה הספציפי הזה:

אז המאמץ גזירה מקסימלי/מינימלי מתקבל כאשר :

תרגיל:
נתון טנזור המאמצים:

  1. מהם המאמצים הראשיים?
  2. מהם מאמצי הגזירה האקסטרימליים?

פתרון:

  1. נציב בנוסחאות: ולכן: כאשר: נוודא שזה הכיוון של המאמץ גזירה, אז נחשב את המישור: והמאמץ בכיוון זה: ולכן הוא אכן הכיוון הנכון ל-.
  2. נציב: את ה- אנחנו לחשב ע”י הצבה, או פשוט ע”י הוספת ל- שקיבלנו בסעיף הקודם:

מישורים ראשיים

האם יש מישורים שעליהם אין גזירה? אנו בעצם שואלים כאן את אותה השאלה ממאמץ נורמלי מקסימלי בדו ממד, אבל עכשיו נרחיב את המקרה לתלת ממד.
אם יש מישורים כאלה, אז וקטור המאמץ חייב להיות בכיוון הוקטור הנורמל למישור, :

אנו גם יודעים כי , ולכן:

נראה מוכר? לא, כי למדנו את זה לפני שנה, אבל זה בעצם ערך עצמי. כיף חיים.
נשים לב כי גם מתקיים , כי במצב זה וקטור המאמץ מתאר את מאמץ הנורמל בכיוון .

הגדרה:

מישורים ראשיים הם מישורים שאין עליהם גזירה, וכיוונם מוגדר ע”י הוקטורים העצמיים של טנזור המאמץ.
המאמץ הנורמלי, , על המישורים הראשיים שווה לערך העצמי המתאים לכיוון המישור הראשי.

מישורים ראשיים ניצבים אחד לשני

נוכיח כי המישורים הראשיים של טנזור הם ניצבים אחד לשני.
יהי ו- שני מישורים ראשיים של כלשהו. אזי:

נחסר בין שתי המשוואות:

נשים לב כי אם פשוט נחליף את האינדקסים (אפשר לעשות כי הם חוזרים, אז אנחנו פשוט מחליפים את “השם” שלהם):

אז נציב:

קיבלנו כי:

במקרה המיוחד השמאלי נדון בהמשך. עבור :

ולכן מתקיים:

ולכן הוקטורים העצמיים של יוצרים שלישייה אורתונורמלית (נזכיר, הוקטורים העצמיים מגדירים את המישורים הראשיים, ולכן הם הו”ע אורתונורמליים, אז גם המישורים ניצבים אחד לשני).

מאמץ נורמלי מקסימלי

המאמץ הנורמלי במישור נתון ע”י:

כלומר, הוא פונקציה שתלויה ב-, כאשר נשים לב שישנו אילוץ על ה--ים - הם רכיבים של וקטור יחידה, כלומר:

אנחנו רוצים למצוא את הערכים המקסימליים של פונקציה רב משתנית תחת אילוץ. זאת בעיה שפותרים עם כופלי לגראנז’:

כאשר סימנו ב- את הכופל לגראנז’.
קיבלנו את המערכת משוואות:

מהמשוואה הראשונה (שהיא למעשה שלוש, אחת עבור כל ):

נשים לב כי , ולכן קיבלנו:

נצמצם אינדקסים חוזרים:

נציב בחזרה:

וקיבלנו:

קיבלנו שתנאי ל- לאקסטרמום הוא ש- מישור ראשי.

  • ישנם שלושה מישורים ראשיים, שלכל אחד מהם מאמץ נורמלי (ע”ע) מתאים.
  • המישור הראשי שמתאים לע”ע הגדול ביותר הוא המישור שעליו פועל המקסימלי. באותו אופן עבור מינימלי.

לכן, אם היינו מחשבים את טנזור המאמצים בכיוונים של המישורים הראשיים, הוא ייראה כך:

מאמץ גזירה מקסימלי

נרשום ביטוי לרכיב הגזירה על מישור , בכיוון וקטור שהוא ניצב לוקטור :

כאשר נשים לב לאילוצים:

עוד פעם כופלי לגראנז’:

נגזור, ונקבל 9 משוואות עם 9 נעלמים. לספי לא היה כוח לעשות את זה.

נקבל שישנם 3 מישורים “חשודים” עבור מאמץ גזירה מקסימלי: מישורים שיוצרים ביחס לכל צמד מהשלישייה (המישורים הראשיים):

נסמן את מאמץ הנורמל במישור ב-.
מאמץ הגזירה על המישור :

מאמץ נורמל על מישור :

אם נגדיר:

אז מאמץ הגזירה המקסימלי יתקבל על מישור:

בנוסף, כיוון הוא מהמישור המינימלי אל המקסימלי.

הערה:

ראינו כי מאמץ הנורמלי המקסימלי מתקבל במישור בו אין מאמץ גזירה. אבל, המקרה ההפוך לא בהכרח נכון. במישור בו המאמץ גזירה מקסימלי, יכל להיות מאמץ נורמלי.

תרגיל:
נתון טנזור המאמצים:

  1. מהם המאמצים הראשיים?
  2. מהם הכיוונים הראשיים?
  3. מהם מאמצי ומישורי הגזירה האקסטרימליים?

פתרון:

  1. נחשב ע”ע: אנחנו נקבל:
  2. נחשב כיוון של : כאשר נזכור כי הוא וקטור כיוון: נקבל: נבצע את אותו החישוב ל- ו- ונקבל:
  3. נציב בנוסחאות: והמאמצים הנורמליים במישורים אילו:

תרגיל
נתון הטנזור:

מהו המאמץ הנורמלי ומאמץ הגזירה על מישור:

פתרון:

קיבלנו כי כל על כל מישור בכיוון שנמצא על המישור , המאמץ הנורמל שווה ל-.

מאמץ הגזירה:

ולכן כל מישור ב- הוא מישור ראשי (אין עליו גזירה).

עמודים המציינים את העמוד הזה