הקדמה - הגדרות ופעולות
עיקרון הסכימה של איינשטיין
הסכם הסכימה של איינשטיין הוא פשוט דרך קצרה לרשום סכומים.
לפי הסכם זה, כאשר אינדקס (למשל
אפשר לרשום בצורה הקצרה הבאה:
כאשר נשים לב שהאינדקסים העליונים הם לא חזקות, אלא אינדקסים של קואורדינטות - כלומר, הכוונה ב-
אז איך יודעים שמפסיקים את הסכימה בשלוש?
בקורס הזה לרוב נניח שמפסיקים את הסכימה בשלוש, כי לרוב נשתמש בקואורדינטות קרטזיות, בהם יש שלושה וקטורים בת”ל. בגדול, אפשר להבין מההקשר מתי מפסיקים לרשום.
עוד דוגמה:
או למשל:
במקרה ויש לנו משתנה שמופיע פעם אחת, כמו בדוגמה הזאת (
דוגמה:
הדלתא של קרונקר
הגדרה:
הדלתא של קרונקר, המסומנת ב-
, מוגדרת כך:
במילים אחרות, המטריצה של דלתת קרונקר היא מטריצת היחידה:
דוגמה:
טנזור המאמץ
חתך בזווית
נביט בדג”ח הבא:
ונביט בחתך:
כפי שאנו מכירים ממכניקת מוצקים 1, ניתן לפרק את גודל הכוח
אבל מה אם נבצע חתך שלא ניצב לכיוון הכוח? להלן חתך בזווית
נשים לב כי שטח החתך משתנה, והוא קשור גאומטרית לשטח הקודם שלנו:
מאחר ועדיין מתקיים:
נוכל להסיק כי גם מתקיים הקשר הבא:
וקטור נורמל לחתך
מאחר והמאמצים והשטחים כל כך תלויים בכיוון של החתך, יהיה לנו נוח להגדיר תמיד וקטור נורמל לחתך
כאשר סימנו:
אם נחזור לביטוי (2):
וקטור הטרחה/מאמץ
הגדרה:
וקטור הטרחה/מאמץ
הוא וקטור העומס המפורש שפועל בנקודה בחתך:
תחשבו פשוט המאמץ, כולל הכיוון שלו.
מאחר ווקטור ההטחרה תלוי ב-
חתכים בדו ממד
נביט בגוף הכללי הבא:
ננתח מה קורה בסביבת נקודה אינפיטסימלית בתוך החומר (נחתוך בשלוש צלעות):
כאשר נשים לב כי:
ולצלע הארוכה (היתר) יש שטח חתך
נניח כי הבעיה בשיווי משקל, ולכן:
נזכיר כי וקטורי ההטרחה הם העומס המפורש בנקודה מסויימת, ולכן:
קיבלנו כי אם ידועים וקטורי ההטרחה של שני חתכים (ניצבים), ניתן לחשב את וקטורי ההטרחה בנקודה על כל חתך
בתלת ממד, נוכל לבצע את אותו התרגיל כדי לקבל:
נהוג גם לסמן את הפוקנציות:
כלומר, וקטור הטרחה על חתך בכיוון
לכן נוכל במקרה התלת ממדי לרשום:
רכיבי טנזור המאמץ
נביט באיור הבא:
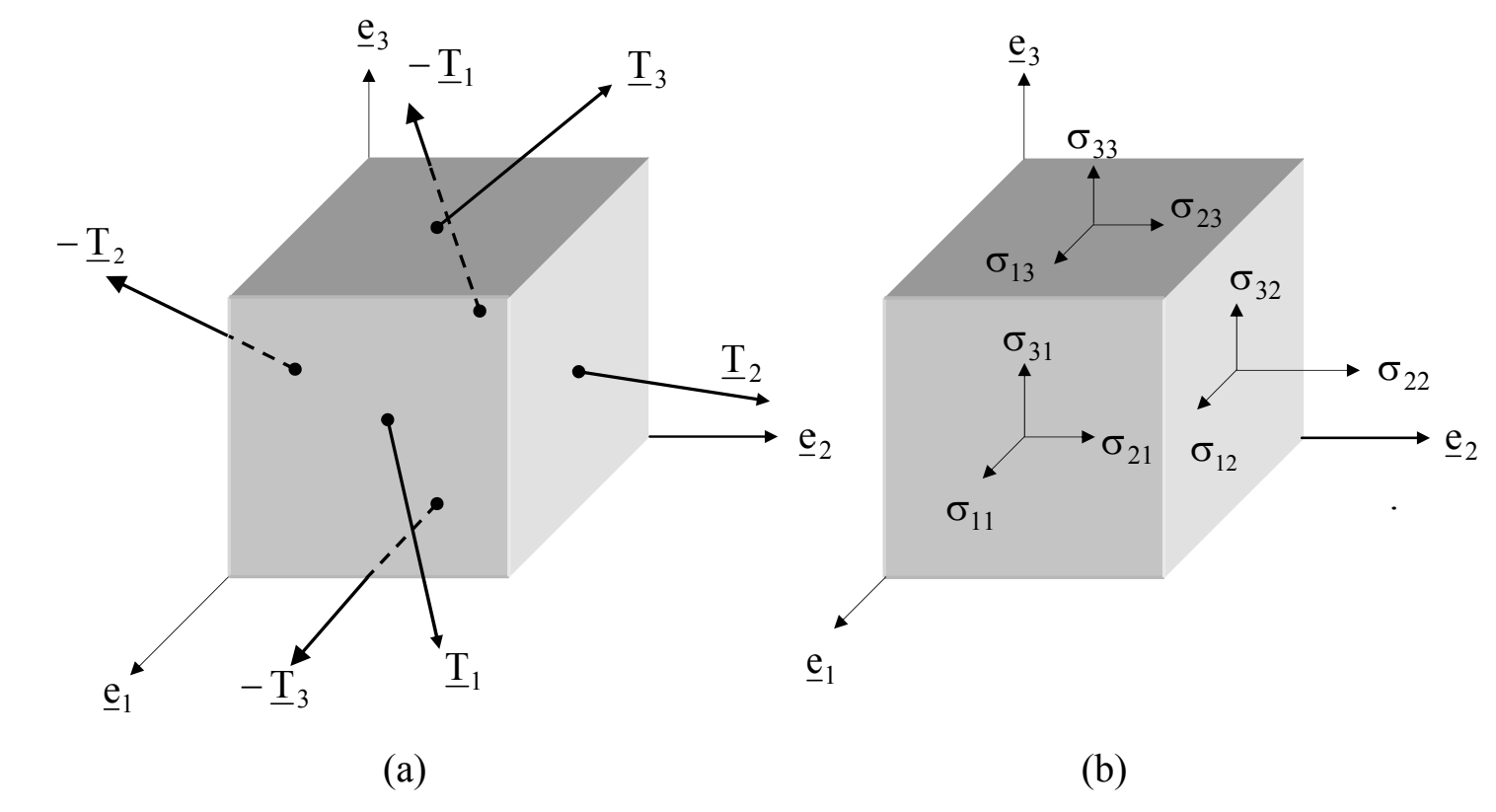
יש לנו כאן חתך תלת ממדי - בשלושה מישורים. בכל אחד מהמישורים האלה, יש וקטור הטרחה משלו, שהוא בעצמו מורכב מעוד שלושה רכיבים.
או בקיצור:
מה זה הסימונים האלה?
אם נציב את (3), נשים לב כי:
אם נפרק לרכיבי
המטריצה שקיבלנו נקראת טנזור המאמץ (
נשים לב כי האינדקס הראשון של
הערה:
טנזור המאמץ מתאר לנו את כלל המאמצים רק בנקודה מסוימת. עבור כל נקודה אחרת הטנזור ייראה אחרת. עבור חומר כללי שמורכב מאינסוף נקודות, ישנם אינסוף טנזורים המתארים את העומסים בכל נקודה.
אם אנחנו רוצים לחלץ את וקטור המאמץ במישור
הערה:
שימו לב כי המכפלה
היא לא מכפלה סקלרית, אלא מכפלה של מטריצה בוקטור.
כעת נוכיח כי מטריצה זו היא למעשה מטריצה סימטרית.
סימטריית הטנזור
נתייחס כעת גם למומנטים:
נבצע כעת חתך אינפיטסימלי בצורת ריבוע:
מהדג”ח ושיווי משקל, נסיק (סכום מומנטים סביב אמצע הריבוע):
אבל מאמץ זה לא כוח, אז איך אתה משתמש בו במשוואות שיווי משקל?
יא חתיכת עיוור אני מכפיל אותו ב-
, יעני האורך/שטח, שהופך את זה לכוח (לפחות מבחינת גודל).
למעשה, נוכל באותו אופן להסיק במקרה התלת ממדי:
ולכן בטנזור המאמץ, מספיק לנו 6 סקלרים כדי להגדיר אותו, מאחר והוא סימטרי:
יש קשר ל טרנספורמציה לינארית?
כן.
סבבה, מה הקשר?
תבין כשתגדל.
פירוק וקטור המאמץ לרכיבים
הערכים באלכסון הראשי הם המאמצים הנורמליים (
אם נתון לנו וקטור מאמץ (
רכיב נורמלי:
הערה:
הביטוי האחרון הוא קיצור לפי הסכם הסכימה של איינשטיין.
רכיב גזירה:
רכיב הגזירה הוא כבר וקטור, מאחר וניתן להגדיר אותו ע”י שני רכיבי מאמץ שמאונכים אחד לשני. נחשבו כך:
הערה:
אם אנחנו בדו ממד, אז נגדיר וקטור
במאונך ל- (אז ). אז רכיב הגזירה שלנו (שהוא עכשיו רק סקלר):
תרגיל
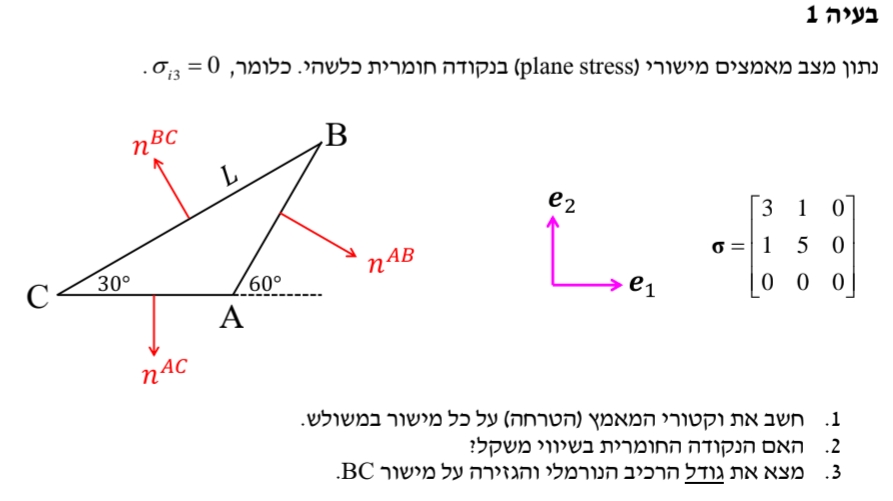
- הנורמל של כל מישור:
- נבדוק את שקול הכוחות, ונראה אם הוא מתאפס:
- נמצא:
תרגיל
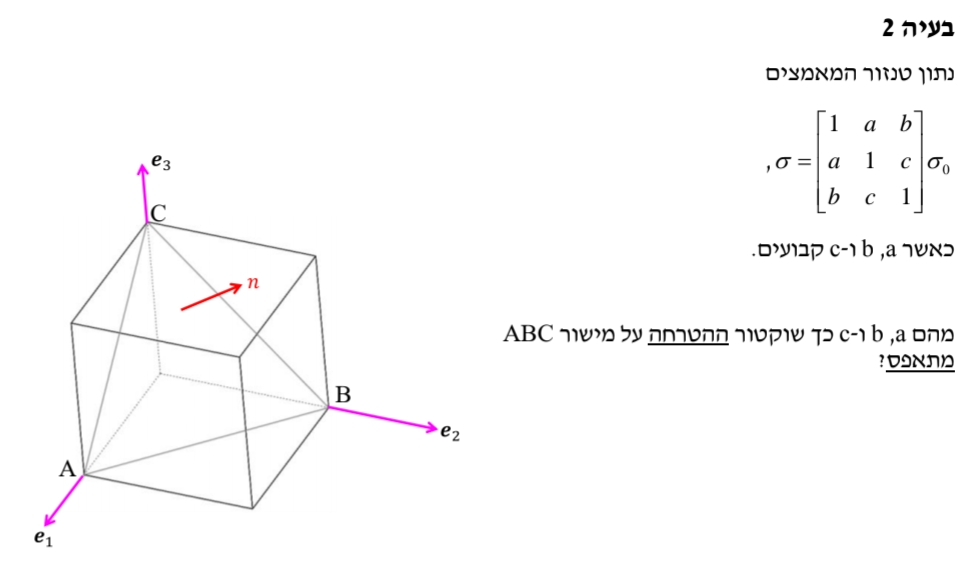
נשים לב כי וקטור הנורמל למישור
נשים לב שזהו לא וקטור יחידה ולכן ננרמל אותו ל-
ולכן:
תרגיל:
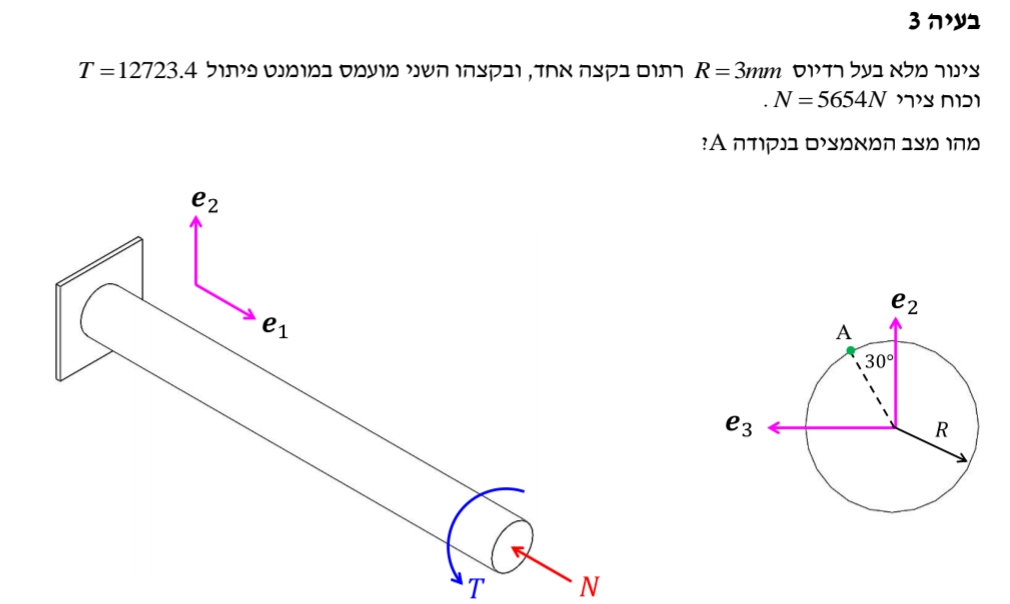
כיוון המישור שלנו הוא
ניזכר מ-מכניקת מוצקים 1 ש:
ולכן:
וכעת נוכל למצוא את
ולכן:
