DVI1_003 עירורים הרמוניים

→ קודם: DVI1_002הבא: DVI1_004 ←

תגובות של מערכת מסדר ראשון לעירורים הרמוניים

משוואת התנועה של מערכת מרוסנת מסדר ראשון, כפי שמתואר באיור הבא, היא:

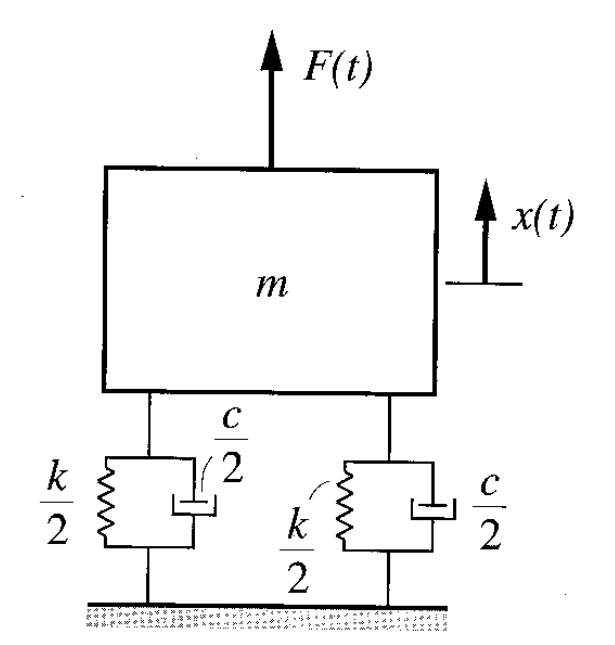
מערכת מרוסנת עם דרגת חופש אחת. (Meirovitch, 2001).

כדי לפתור את מד”ר לא הומוגנית זו אנו יכולים לפתור את המשוואה ההומוגנית המתאימה, בנפרד לכך למצוא פתרון פרטי לבעיה, ואז לחבר לינארית את שתי סוגי הפתרונות כדי לקבל את הפתרון הכללי שלנו. לאחר מכן כל מה שנדרש הוא להציב את תנאי ההתחלה ו-.

נתמקד כעת במקרים בהם הוא כוח הרמוני, שניתן לתארו ע”י:

כאשר בו ה- נקרא תדירות העירור. נשים לב גם של- ו- יש יחידות של תזוזה. נציב את סימון זה במשוואת התנועה כדי לקבל משוואה מהצורה:

כאשר הוא המקדם ריסון הצמיגי ו- הוא התדירות הטבעית של התנודות הלא מרוסנות.

אנו מכירים ממערכות לינאריות שהתגובה לכוח הרמוני, במצב מתמיד, תהיה גם הרמונית. לכן נניח שלפתרון יש הצורה:

כאשר הם קבועים שניתן למצוא מהצבה בחזרה במשוואה. לאחר המון הצבות ואלגברה מעצבנת אנו מקבלים:

כאשר

הוא העוצמה (magnitude) ו-

הוא זווית הפאזה של התגובה במצב מתמיד.
ישנה עוד דרך למציאת ביטוי שקול ל- שמסתמך על זהות אויילר בו אנו מציגים את הכניסה, כ:

עם הצגה זו נגיע לביטוי:

כאשר הוא התגובת תדירות (frequency response) של המערכת:

ו- הוא אותה הפאזה שהגדרנו לעיל.
. כמו במערכות לינאריות, נהוג לפרק את לחלקו המדומה והממשי:

מה שאנו יודעים להציג בדיאגרמות בודה.
אם העירור הוא מהצורה , התגובה היא:

אם העירור הוא מהצורה , אז התגובה היא:

משוואות אלו מגדירות את התגובה ההרמונית במישור הזמן לכל עירור בתדירות . דרך נפוצה (דומה לדיאגרמות בודה) לתאר את הקשר בין העוצמה , פאזה לתדירות היא ע”י שרטוטם ביחס לגודל , שמקיים:

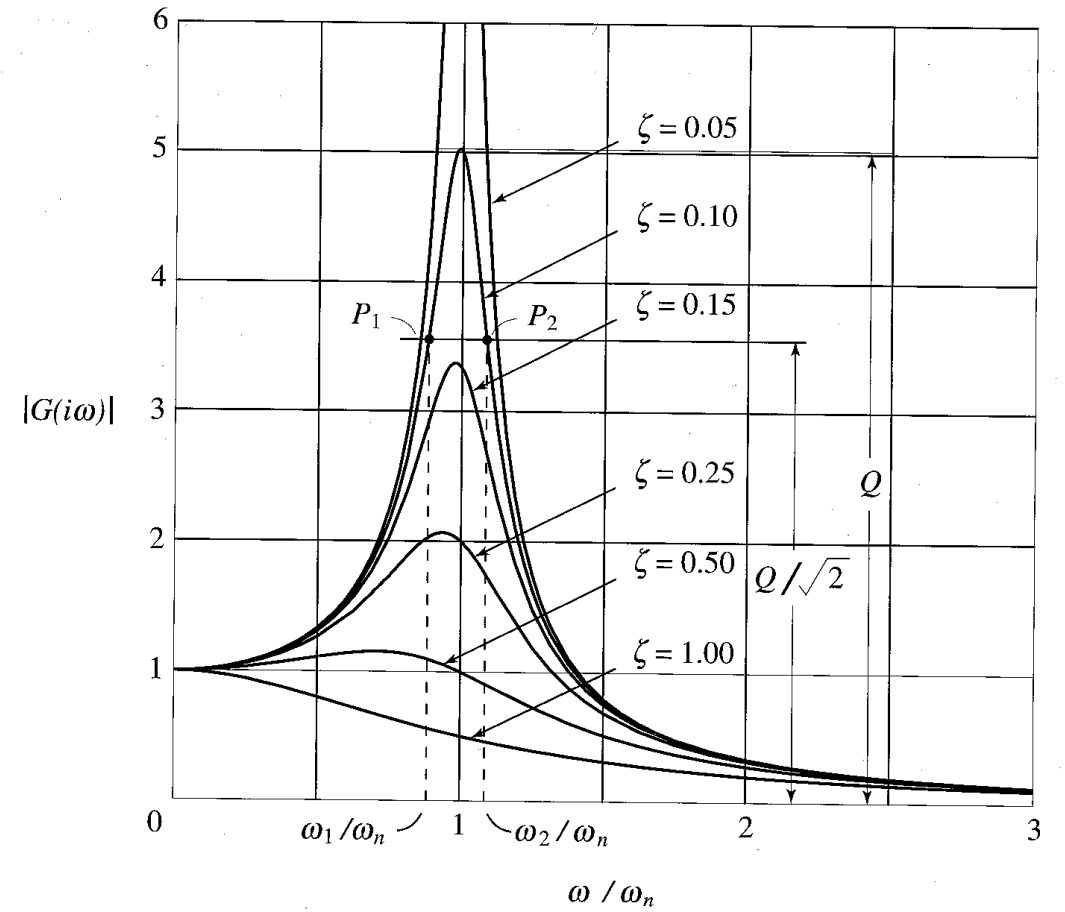
עוצמת התגובת תדירות לערכי שונים. (Meirovitch, 2001).

אנו רואים שכאשר מקדם הריסון , אין לתגובה שיא עבור תדירות מסוימת. במקרה הלא מרוסן, , התגובה גדלה אינסופית כאשר שואף לתדירות הטבעית . במקרה זה אנו אומרים שלמערכת תנאי תהודה (resonance condition), שמאופיינת ברטט עוצמתי.

עבור מסוים אנו יכולים למצוא את האמפליטודה המקסימלית ע”י:

כאשר הריסון קל יחסית, כמו למשל כש- , המקסימום מתרחש יותר באזור של . מעבר לכך, עבור ערכים קטנים של , המשוואה לעיל נותנת את הקירוב

כאשר ידוע כהמקדם איכות, כי בהנדסת חשמל, למשל בכוונון מעגל ברדיו, אנו מעוניינים באמפליטודות בתהודות גדולות ככל האפשר.

לגבי זווית הפאזה :

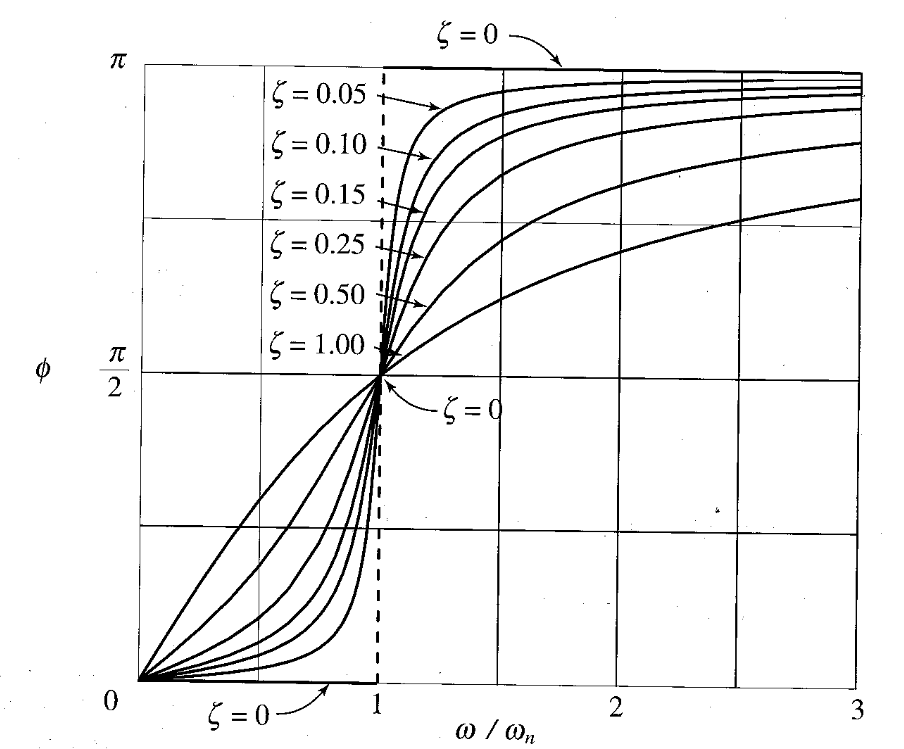
זווית פאזה של תגובת תדירות. (Meirovitch, 2001).

נשים לב שכל העקומות עוברות דרך הנקודה . יתר על כן, עבור , זווית הפאזה שואפת לאפס כאשר , ועבור זווית הפאזה שואפת ל- כאשר .
עבור , הפאזה היא עבור , ויש לה נקודת אי רציפות ב- - היא קופצת מ- ל- ואז ל-, וממשיכה עם ערך זה עבור . נשים לב שאם , נוכל להסיק מהגרף שזווית הפאזה בתהודה היא .

תרגילים

תרגיל 1

מסה מחוברת ע”י קפיץ ומרסן לעגלה בעלת מסה . על המסה פועל כוח מחזורי . נתון כי משוואות התנועה הינן:

סכמת העגלות.

הניחו כי כי העגלה מקובעת, . נבחן את המקרה בו היא לא מקובעת בתרגילים בהמשך הקורס.

סעיף א’

בסעיף זה הניחו כי לא פועל כוח חיצוני. מצאו את התגובה של המערכת לתנאי התחלה של מהירות ומיקום, כאשר אין ריסון.

פתרון:
בהיעדר כוחות חיצוניים וריסון, משוואת התנועה של המסה היא:

נסמן , כך ש:

ננחש פתרון כללי (כמו במד”ר לא הומוגנית עם מקדמים קבועים):

כאשר הוא מספר מרוכב.
נציב את הפתרון אל משוואת התנועה ונקבל:

כלומר, המערכת תתנוד בתדירות הטבעית שלה.
נציב את תנאי ההתחלה בפתרון:

כך שתגובת המערכת שתתקבל:

נפתח סוגריים בעזרת זהות אויילר:

נקבל:

עוד דרך להציג את הפתרון היא בעזרת סינוס בודד:

כאשר:

העשרה (שתאכלס צריכים בהמשך הפתרון, אז אני לא יודע למה מגדירים את זה העשרה):

כאשר המערכת עם ריסון, נקבל:

ננחש פתרון מהצורה . נקבל:

נסמן . כאשר (כלומר, כאשר המערכת תת-מרוסנת):

מהצבת תנאי ההתחלה נקבל פתרון מהצורה:

כאשר:

סעיף ב’

רשמו את משוואות התנועה האל-ממדיות, הציגו את התגובה האל-לממדית לתנאי ההתחלה, כאשר .

פתרון:

כעת נבצע את אותם הפעולות רק עם משוואות אל-ממדיות, ועבור תנאי התחלה .

משוואת התנועה כעת:

נחלק ב-:

נסמן:

כאשר הוא הזמן להשלמת מחזור יחיד - זמן מנורמל.

נחשב את הנגזרות לפי בעזרת כלל השרשרת:

נציב בחזרה במשוואה:

נרצה גם להיפטר מה-, אז מהגדרת נרשום :

נציב בחלק מהמקומות:

בנוסף, נסמן גם:

ולכן:

כדי להיפטר מ- באגף ימין נחלק בגודל זה:

נגדיר קואורדינטה חדשה:

ולכן:

הפתרון הוא סכום הפתרונות ההומוגני ואי הומוגני (פרטי). הפתרון ההומוגני למשוואה הוא פתרון שמצאנו בהעשרה (רק נצטרך לנרמל אותו):

ע”פ משפט תגובת התדירות, ננחש פתרון פרטי מהצורה , נציב במד”ר וניקח רק את החלק הממשי בסוף הפתרון:

נשים לב ש- , ולכן:

נוכל לפרק את לגודל סינוסואידי:

כאשר:

ולכן הפתרון הפרטי:

והפתרון הכללי:

נשים לב שהפתרון במצב מתמיד מקיים:

כלומר קיבלנו תגובת מעבר (transient) שדועכת לאחר זמן.

סעיף ג’

בהינתן , פתחו ביטויים לתגובת התדר של המיקום, המהירות והתאוצה כפונקציה של אמפליטודת האילוץ במצב מתמיד.

פתרון:
תגובת תדירות של מיקום (במצב מתמיד) מצאנו כבר. זהו הפתרון הפרטי:

כאשר:

המהירות:

נרצה לדעת עבור איזו תדירות מקבלים מהירות מקסימלית. נשים לב שגודל המהירות בריבוע:

נשים לב שככל ש- נקבל יותר גדול, מה שאומר שנקבל מהירות מקסימלית עבור (נובע מהגדרת ). האמפליטודה והפאזה של :

סעיף ד’

ציירו את ההגבר והפאזה של תגובות התדר עבור המהירות.

פתרון:

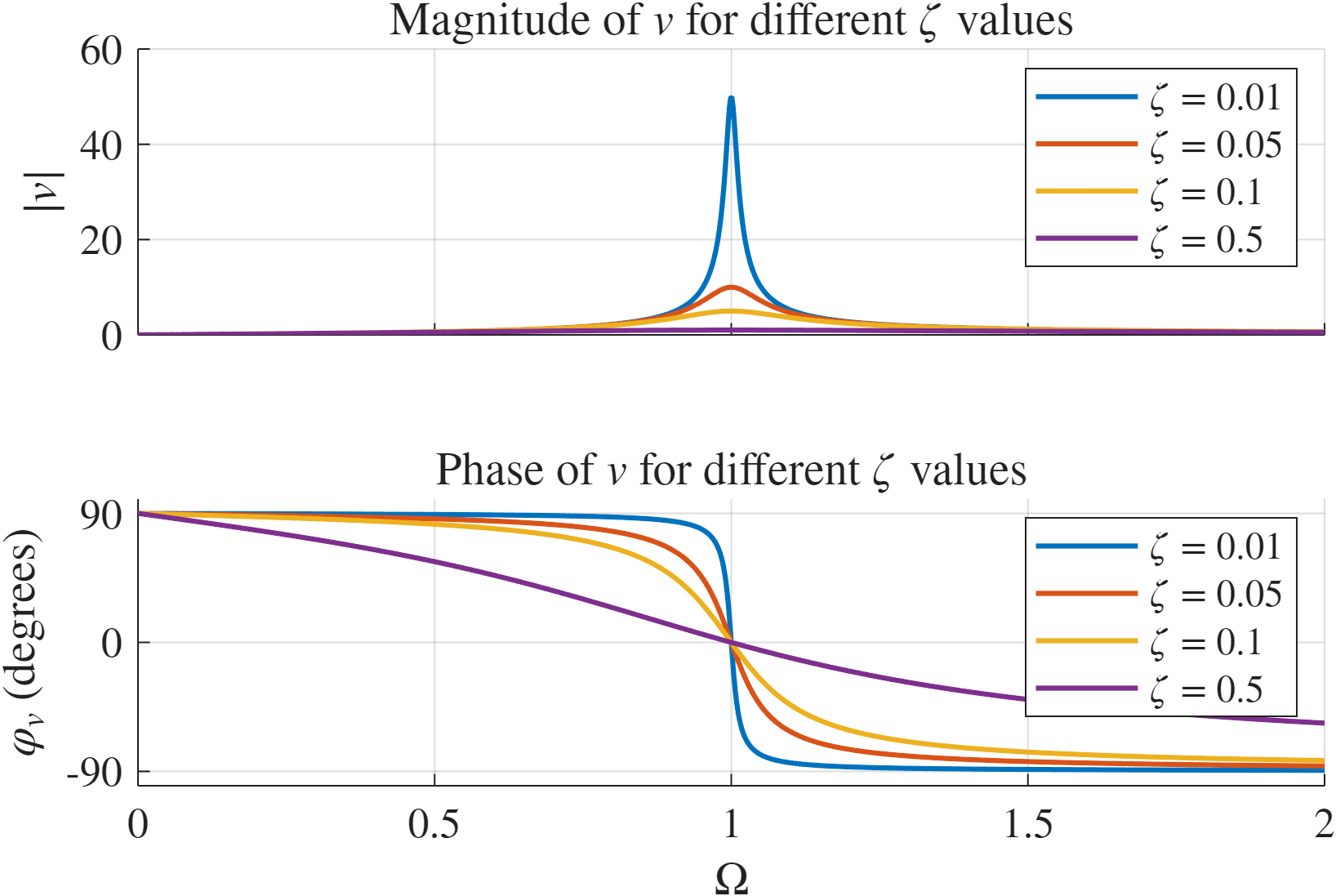
דיאגרמת בודה (אבל לא ב-) עבור .

הקוד נמצא בGitHub.

נשים לב ש:

• המערכת נכנסת לתהודה (resonance) עם התקרבות התדירות המנורמלת ל-, כלומר כאשר , כפי שראינו בסעיף קודם.
• הקטנת הריסון מתבטאת בגידול משמעותי באמפליטודה.
• עקומי האמפליטודה נחתכים ב-. חיתוך זה מחלק את העקום לשני תחומים. הוא תחום ההגברה (amplification region). ככל שהריסון קטן כך אופן התגובה גדלה. הוא תחום השיכוך (isolation region), בו ככל שהריסון קטן יותר כך אמפליטודת התגובה קטנה.
• קצב התכנסות הפאזה תלוי בריסון. ככל שמנת הריסון נמוכה יותר כך הפאזה מתכנסת עבור תדירות היותר קרובה ל-.

→ קודם: DVI1_002הבא: DVI1_004 ←