פנגייה

LSY1_004 Linear State-Space Equation

• זמן קריאה: 21 דק'

Impulse Response

The impulse response of a dynamic system is its output when presented with a brief input signal (unit impulse) - . More generally, an impulse response is the reaction of any dynamic system in response to some external change.
book

The impulse response from a simple audio system. Showing, from top to bottom, the original impulse, the response after high frequency boosting, and the response after low frequency boosting.

The output of a CLTI system is completely determined by the input and the system’s response to a unit impulse.

We can determine the system’s output if we know the system’s impulse response and the input .

In fact, we can show that by convolving the input with the impulse response of the system we get the system’s output :

Examples:

  1. For the gain system , the impulse response is:
  1. For the delay system , the impulse response is:
  1. For the integrator system , the impulse response is:
𝟙
  1. For the finite-memory integrator , the impulse response is:

Causality via Impulse Responses

Theorem

A CLTI system with the impulse response is causal iff .

Proof:
The response reads at every as

The future term zeros out iff for all . i.e., for all , which is equivalent to saying .
Thus, cannot depend on for iff - the system is causal.

Stability via Impulse Responses

Theorem

A CLTI system with impulse response is BIBO stable iff . If the system is BIBO stable, then

Notes:

  1. The mere decaying of might not be enough for the BIBO stability of . For example, if
𝟙𝟙

then for all

𝟙

and it is not bounded. Hence, this system is not BIBO stable (and indeed ).
2. The -stability is not easy to verify directly in terms of the impulse response (need frequency domain).

Linear State-Space Equation

In state-space linear systems we were to introduced to the CLTI state-space equation. In the case of SISO (single-input, single-output), we have the following first-order differential system:

Where .
This quadruple is called a state-space realization of the system.
Although we have shown the the solution of a linear set of differential equations defines a linear input/output system, we have not fully computed the solution of the system.
In fact, it can be shown that the solution of such system is:

Where we have a matrix exponential - . To show that this is the solution of the given ODE, we first need to go over what is a matrix exponential.

The Matrix Exponential

Definition:

The matrix exponential is defined as the infinite series

where .

It can be shown that the series in the definition converges for any matrix in the same way that the normal exponential is defined for any scalar .

Example:

Compute the matrix if the matrix has the form
1.

Solution:
1.

Properties of the Matrix Exponential

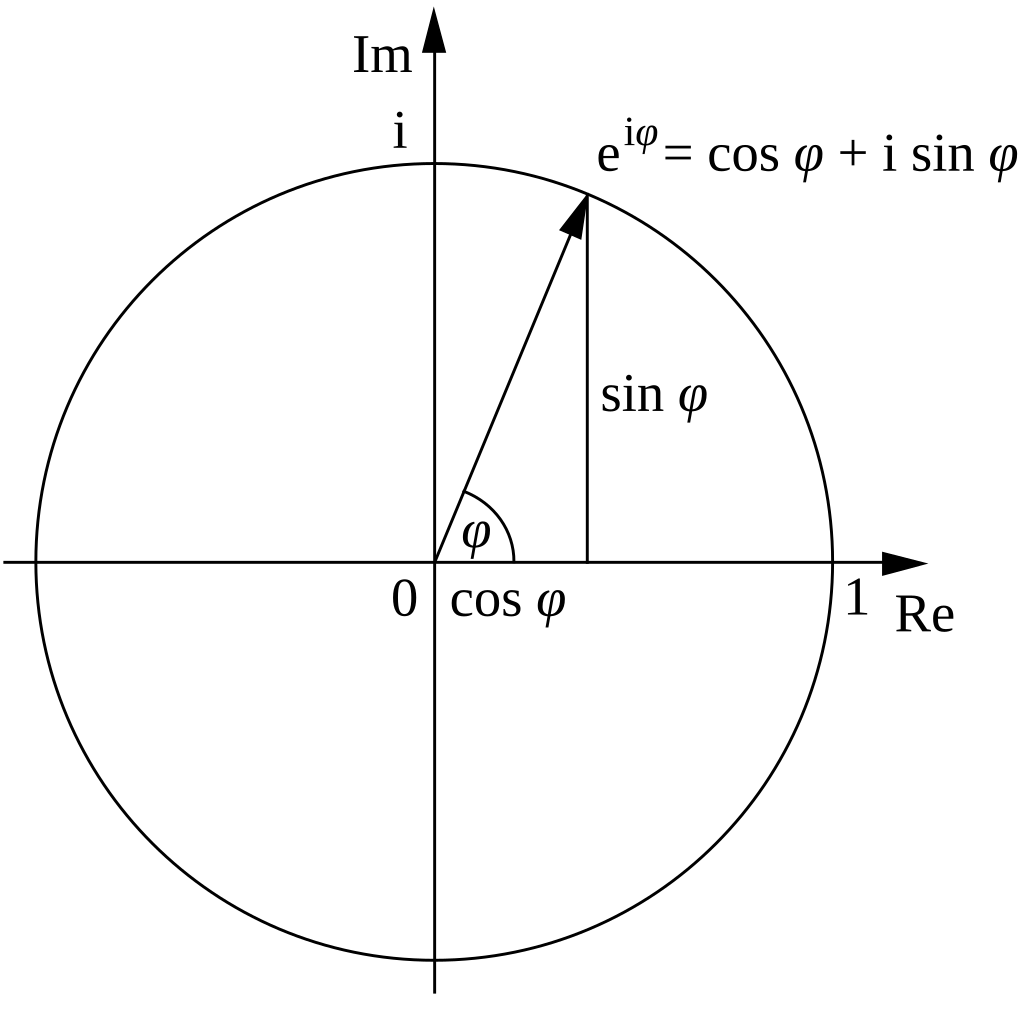
Euler’s Formula

formula:

Euler’s formula states that

book

Attention!

We write instead of because of aliens.
These aliens refer to themselves as ‘electrical engineers’. They use to denote their precious little electrical current. Very confusing.

Some important identities derived from this definition are:

Special Matrix Exponential

Let

Finding its eigenvalues and eigenvectors, we get:

Which is why its exponential:

Applying Euler’s Formula, we get

Because of the equality , we can say that:

Calculating the Matrix Exponent

It won’t always be simple to calculate for any given using the definition. An easier way would be to diagonalize , and then use a special property of diagonalizable matrices:

which would simple entail the calculation of multiplying 3 matrices.
Another way would be to do it via Cayley-Hamilton:

where

The matrix is called the Vandermonde matrix. We won’t go about how the Cayley-Hamilton method is derived, but be assured, it has something to do with Cayley-Hamilton theorem.

Real Diagonalization of a Matrix with Complex Eigenvalues

In both cases we need to find the eigenvalues of . If it has only real-valued eigenvalues, we’re good - we already know how to approach such cases.
But, if there is a pair of complex eigenvalues , then we also have two complex conjugate eigenvectors where are real valued vectors.

We now show a special representation of the matrix called real diagonalization of a matrix with complex eigenvalues. We first define two linear combinations of our eigenvectors:

Defining

we get that

When this form of “diagonalizing” of the entire matrix , we get with either real eigenvalues or block of -s on the main diagonal:

Now, we know that:

Solution to State-Equation

Consider the function

According to the Liebniz integral rule, and the chain rule,

and the relation , we have that

Which is exactly the state equation. We can plug it into the Linear State-Space Equation, to get its solution:

and the Impulse Response is given by:

𝟙

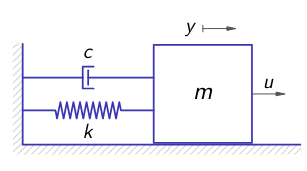
Example: Mass-Spring-Damper System

book

mass-spring-damper system. The mass is connected to a spring with stiffness and a viscous damper with damping coefficient .

The input to this system is the force applied to the mass, and the output is the position of the mass.
Supposing zero spring and damper forces at , by Newton’s second law:

Introducing the vector allows to describe the system by state-space representation:

If :

We would like to find the impulse response of this system. Therefore, we need to look at :
Eigenvalues of :

  • If , then :
    can be written as

and its matrix exponential is

Therefore, the impulse response is:

𝟙𝟙

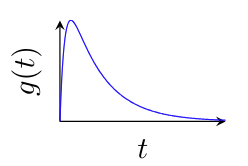
If , we get , and the impulse response looks like
book
which we call this overdamping - If the damping coefficient is significantly larger than the spring stiffness, when we jerk the mass to the right (we give it an impulse), the mass will slowly return back to its original position.

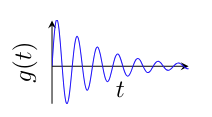
If , we get and . Let , then the impulse response is

that looks like
book
which we call underdamping - when we jerk the mass to the right, the mass will oscillate back and forth.

  • If , then and
𝟙

look like
book
and is called critical damping - the boundary between overdamping and underdamping.

Transfer Function

A transfer function is a function that models the system’s output for each possible input.

Transfer Function to State Space

Physical realization

Given a system with following transfer function:

then its possible state-space realization is:

Canonical Realization

For the following ODE:

The state-space realization discussed above, known as the companion form, is:

Its space-state realization in observer form has

If on the right side of the equation there is an derivative of , that is there is a term where , we can write the same canonical realization as for the system with , and simple change .

Exercises

Question 1

Consider the matrix:

Part a

Find the diagonalizing transformation of (if the real form if it exists).

Solution:
First, calculate the characteristic polynomial:

Now we can calculate the eigenvectos:

  • For :
  • For :
  • For : Hence, the diagonalizing transformation of : And:

Part b

Calculate the matrix exponent using diagonalization.

Solution:
We’ll find first:

All that’s left is pain:

Part c

Calculate the matrix exponent using Cayley-Hamilton.

Solution:
According to Cayley-Hamilton, we know that:

Using , we can find that these coefficients satisfy:

We can write it as:

We can move to the left side:

Remember the obscure matrix operation to find its inverse, the adjoint matrix? Here you go:

And we get:

All that’s left is pain:

Question 2

Consider the following ODE:

Part a

Perform a reduction of order to the ODE and write it down in state-space form.

Solution:
Define:

In state-space form:

Part b

Find the diagonalizing transformation (in the real form if it exists) of the matrix

Solution:
First, we’ll find the eigenvalues:

The corresponding eigenvectors:

  • for : If we choose , we get therefore:
  • for : If we choose , we get therefore:

Since we have complex eigenvectors, we need to perform a real diagonalization. Define:

Therefore:

And the real diagonal matrix is:

Part c

Find the matrix exponential .

Solution:
We know that:

Substituting from previous answers:

For a matrix, we can calculate the inverse using adjoint matrix:

we get:

Part d

Find the impulse response. hint:

Solution:
The Impulse Response is given by:

𝟙

In our case:

𝟙𝟙𝟙

we get:

𝟙

Part e

Determine whether this system is BIBO stable.

Solution:
To find whether a system is BIBO stable, we can check if :

𝟙

We know that . Therefore, we get

and can conclude that . That is, the system is BIBO stable.

Question 3

Let be the matrix:

Part a

Find the diagonalizing transformation (in the real form if it exists).

Solution:

We first find the eigenvectors and eigenvalues:

Therefore, the eigenvalues are:

Now, to find the eigenvectors:

  • For : which means
  • For : which means
  • For , we know that is the complex conjugate of , which means .

The real diagonal matrix is:

And the transformation matrix is:

Part b

Find the matrix exponential .

Solution:
Now we can find the matrix exponent:

No real point in developing this any further.

Question 4

Given the following second-order differential equation

Part a

Find a physical state-space realization.

Solution:
Define

so we can write (using reduction of order):

Or, using the formula:

Part b

Use this state-space model to calculate the impulse response of the system.

Solution:
The impulse response can be given by:

𝟙

In our case:

𝟙

We have seen that

so in our case:

𝟙𝟙

Question 5

Consider the following ODE:

Part a

Find the state-space realization in companion form.

Solution:
According to the formula:

Part b

Use the following transformation matrix to get a similar realization:

What does this similar realization correspond to?

Solution:
The inverse of (using adjoint):

So the similar realization:

The similar realization correspond the observer form of the canonical realization.

עמודים המציינים את העמוד הזה