DYN1_002 קינמטיקה של חלקיק - מערכת צירים סובבת

→ קודם: DYN1_001הבא: DYN1_003 ←

מערכת קואורדינטות נעה, ומערכת וקטורי בסיס סובבת

סיבוב סופי

סיבוב סופי אינו קומוטטיבי.

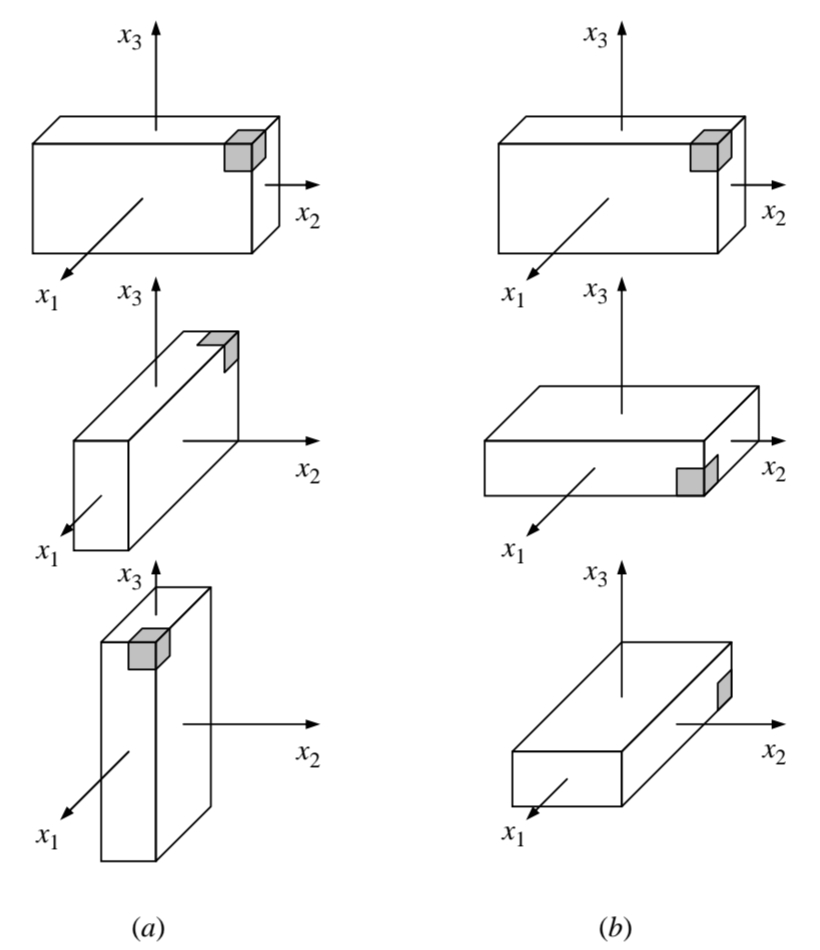
המחשת האי-קומוטטיביות של סיבוב סופי. סיבוב סופי סביב ציר ולאחריו סיבוב סופי סביב , סיבוב סופי סביב ציר ולאחריו סיבוב סופי סביב (Elata, 2002).

כאשר מבצעים שני סיבובים סופיים עוקבים התוצאה הסופית תלויה בסדר בו מבצעים את שתי פעולות הסיבוב.

סיבוב אינפיניטסימלי

סיבוב אינפיניטסימלי הוא פעולה קומוטטיבית - סדר הפעולות לא משנה. האיור הבא מסביר זאת:

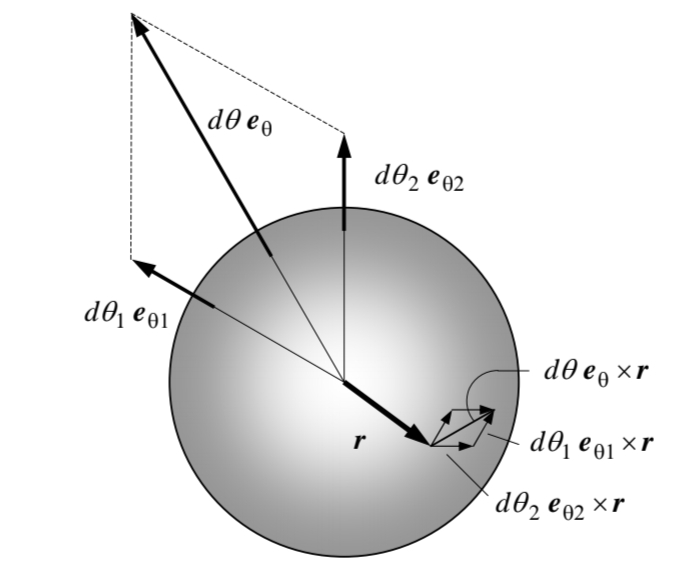
שינוי זווית אינפיניטסימלי (Elata, 2002).

עבור זוויות קטנות מספיק, מתקיים:

טנזורי הסיבוב עבור כל זווית יהיו מהצורה:

נקבל כי אין חשיבות לסדר ההכפלות:

מערכת וקטורי בסיס סובבת

נסתכל על וקטור בסיס במערכת סובבת (או מסתובבת) , ונרצה לחשב את קצב הסיבוב שלו. את מערכת הצירים המסתובבת (שמשתנה עם הזמן) נוכל להגדיר כ:

כאשר , שזה בעצם סיבוב המערכת הצירים בטווח הזמן .
נחזור לחדו”א 1, לפיו הגדרת הנגזרת:

נסמן . נוכל לרשום את המשוואה באופן מטריצי:

נסמן את וקטור המהירות הזווית . כיוון שאנו במערכת , נשתמש בסימון (זוהי סכימה לפי איינשטיין!). כעת נוכל לרשום את המכפלה הזאת בצורה וקטורית:

הוקטור הינו וקטור המהירות הזוויתי הרגעית של מערכת הצירים , מבוטאת ברכיבים במערכת .

הערה:

בספרויות שונות כאשר משתמשים בנגזרת זו, במקום , מורידים את הסימון , ומשתמשים באות הקטנה . אנו מסמנים כך כדי להדגיש את העובדה שאנו במערכת , וכדי להבדיל מסיבוב של גוף קשיח שמסומן ב-, שנלמד בהמשך.

כלל האופרטור

בהינתן וקטור על ידי רכיביו במערכת סובבת:

כאשר נגזור אותו נקבל:

כאשר הוא קצב הסיבוב של המערכת .
נשים לב כי יש לנו כאן דו משמעות בסימונים שלנו - ו-. לכן, את הגזירה של הוקטור ביחס למערכת הכיוונים הסובבת באופן . המשוואה הקודמת תרשם לפיכך באופן:

משוואה זו נקראת כלל האופרטור (הנגזרת) והיא מתארת את מימוש הנגזרת המוחלטת במערכת וקטורי בסיס סובבת. הביטוי נקרא נגזרת בסיס (frame derivative) והוא מבטא את הנגזרת בזמן של רכיבי הוקטור הנתונים במערכת סובבת . האיבר הוא תרומה לקצב השינוי של עקב סיבוב המערכת .

דוגמה: קינמטיקה של חלקיק במערכת צירים פולרית (גלילית)

חלקיק נע בתנועה מישורת המתוארת ע”י קואורדינטות פולריות . דרוש לבטא את וקטורי המיקום, מהירות ותאוצה במערכת הצירים הפולרית .
הבעיה היא מישורית, ולכן וקטור המהירות הזוויתית של מערכת הצירים נתון ע”י .
וקטור המיקום יהיה .
לכן וקטור המהירות ע”פ כלל האופרטור:

בזהות מוחלטת למה שקיבלנו בקואורדינטות פולאריות.
עבור התאוצה נפעיל שוב את כלל האופרטור:

שגם זה זהה למה שקיבלנו בקואורדינטות פולאריות.

דוגמה: חישוב נגזרת של וקטור המהירות הזוויתית של מערכת הצירים

לפי כלל האופרטור:

דוגמה: וקטור נגזרת שנייה במערכת סובבת

נתון:

דרוש לחשב נגזרת שנייה בזמן לפי כלל האופרטור.

נפעיל שוב את כלל האופרטור:

קיבלנו את נוסחת 4 האיברים לתאוצה במערכת סובבת:

דוגמה: חישוב תאוצה במערכת כדורית עבור מקרה ספציפי

מסלול של חלקיק על מעטפת כדור נתון בקואורדינטות כדוריות ע”י:

כאשר קבוע ו- קבוע. דרוש לבטא את במערכת צירים כדורית.
וקטור המיקום שלנו יהיה .
לפני שנשתמש בכלל האופרטור, עלינו למצוא את . במקרה שלנו, נוכל לתאר את בקואורדינטות גליליות:

נרצה לעבור לקואורדינטות כדוריות. נשים לב ש- , ולכן:

כעת, לפי כלל האופרטור, המהירות תהיה נתונה ע”י:

נפעיל שוב את הכלל בשביל התאוצה:

כאשר הוא הכיוון הרדיאלי במערכת הגלילית, והוא מקיים:

תרגילים

שאלה 1

גלגל ברדיוס מסתובב בקצב קבוע ביחס לזרוע סביב ציר .
הזרוע שאורכה מסתובבת בקצב קבוע ביחס לזרוע סביב ציר .
הזרוע שאורכה מסתובבת בקצב קבוע ביחס למרחב המוחלט סביב ציר .
מערכת הצירים צמודה לזרוע ומערכת צמודה לזרוע .
ברגע נתון כי .

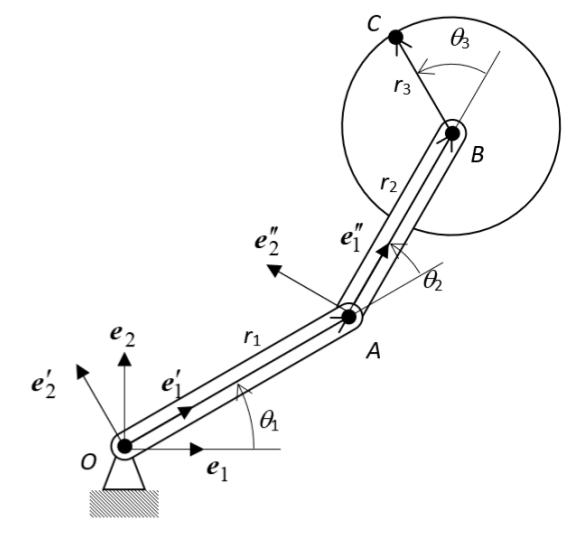
סכמת הבעיה

סעיף א’

חשבו את המהירות המוחלטת והתאוצה המוחלטת של נקודה ברכיבי המערכת .
פתרון:
נגדיר את וקטורי המהירות הזוויתית של שתי המערכות:

עבור , הזווית הכוללת של המערכות ביחס למערכת הנייחת היא . עבור , הזווית הכוללת היא . לכן וקטורי המהירות הזוויתית יהיו:

וקטור המיקום של נקודה :

נוכל לבטא את במערכת :

לכן:

לפי כלל האופרטור:

נשתמש בטבלה:

לכן וקטורי המהירות והתאוצה:

סעיף ב’

חשבו את התאוצה היחסית של נקודה ביחס לנקודה ברכיבי המערכת .
פתרון:
נביע את המיקום היחסי במערכת :

כעת כאשר נגזור לפי כלל האופרטור, נצטרך לגזור לפי המהירות הזוויתית של , שהיא :

נבנה טבלה:

לכן:

ביקשו במערכת :

סעיף ג’

חשבו את המהירות של נקודה ביחס לנקודה , ברכיבי מערכת אחת כבחירתך.
פתרון:
נבנה מערכת , כך ש- צמוד ל-. לכן:

לכן מיקום ביחס ל-:

לפי כלל האופרטור:

נקבל כי:

סעיף ד’

חשבו את המהירות המוחלטת של נקודה ברכיבי מערכת אחת כבחירתך, מהי המהירות ברגע ?
פתרון:
בכל מערכת צירים:

הערה:

ביקשו מהירות מוחלטת, ולכן כאשר אנו רושמים למשל אנו מתכוונים ל- - כלומר למהירות של ביחס לנקודה קבועה.

נמצא את במערכת . מסעיפים קודמים, אנו יכולים למצוא את ו- במערכת :

נציב:

את כבר יש לנו:

ולכן:

נציב :

סעיף ה’

חשבו את המהירות של נקודה כפי שהיא נצפית ע”י מצלמות הצמודות למערכת (המהירות הנצפית של נקודה ביחס למערכת ).
פתרון:
מנקודת המבט של המצלמות, המערכת הינה מערכת “נייחת”, ניזכר בכלל האופרטור:

כלומר, נחשב רק את . מיקום :

נמצא את נגזרת הבסיס:

שאלה 2

אל מוט טלסקופי , מחוברת טבעת בעלת רדיוס ומרכזה בנקודה . מנגנון המכניזם ניתן לתיאור בצורה הבאה:

• החלק של המוט מסתובב במהירות זוויתית קבועה סביב ציר אנכי.
• הטבעת מסתובבת במהירות זוויתי קבועה סביב הציר .
• מרכז הטבעת , מתרחק מהנקודה במהירות קבועה .

הנקודה הינה חיתוך ציר עם הטבעת. על הטבעת מחליק חרוז כך שמיקומו (זווית ) נתון כפונקציה של הזמן. עבור זמן , מתקיים ו- .

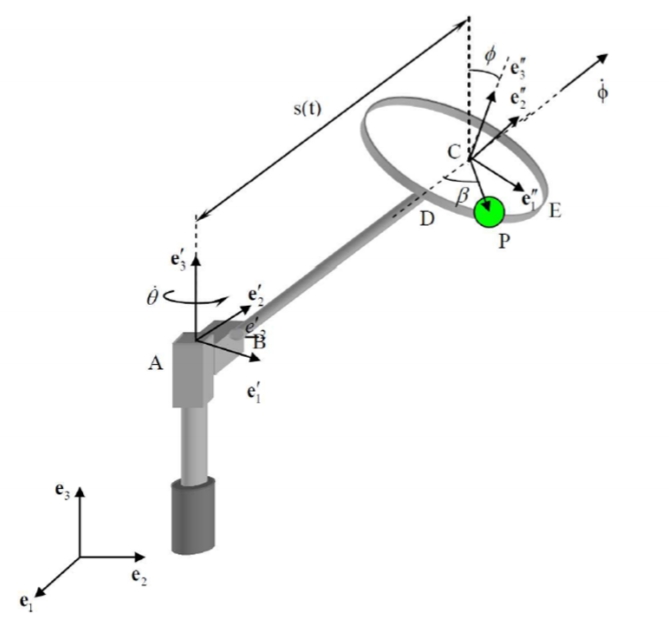
סכמת הבעיה

סעיף א’

מהי המהירות הזוויתית המוחלטת של הטבעת?
פתרון:
אנו יודעים כי צמוד ל-. לכן:

לגבי מערכת הצירים :

לכן המהירות הזוויתית של הטבעת:

כאשר נשים לב ש:

סעיף ב’

מהי התאוצה הזוויתית המוחלטת של הטבעת?
פתרון:
מבקשים למצוא את התאוצה של הטבעת. כלומר, עלינו לגזור את :

נקבל (לאחר טבלה) כי:

סעיף ג’

מהי המהירות המוחלטת והתאוצה המוחלטת של נקודה הצמודה לטבעת? חשבו אותן עבור .
פתרון:
מיקום הנקודה :

נבחר לייצג את המהירות המוחלטת במערכת . נשים לב כי:

לכן:

נגזור לפי כלל האופרטור:

נקבל כי:

נציב את תנאי ההתחלה בזמן :

→ קודם: DYN1_001הבא: DYN1_003 ←