HTF1_E2024WA 2024 חורף מועד א'

שאלה 1

סעיף א’

סכמת הבעיה.

נתונים:

פתרון:
מחוק הראשון של התרמודינמיקה, בהנחה ואין ייצור חום פנימי וההולכה חד-ממדית:

לכן נוכל לרשום גם:

לפי חוק פורייה:

נמצא כי:

ולכן:

אנו יודעים מהו ב-. לכן, נציב זאת ב-(1.1):

סעיף ב’

נתונים:

תכונות המים ב-:

נחשב את צריכת החשמל היומית של המשפחה כתוצאה מחימום המים. לפי משוואה (IH1.12e):

לאחר אינטגרציה לפי זמן:

ולכן המחיר לשנה:

סעיף ג’

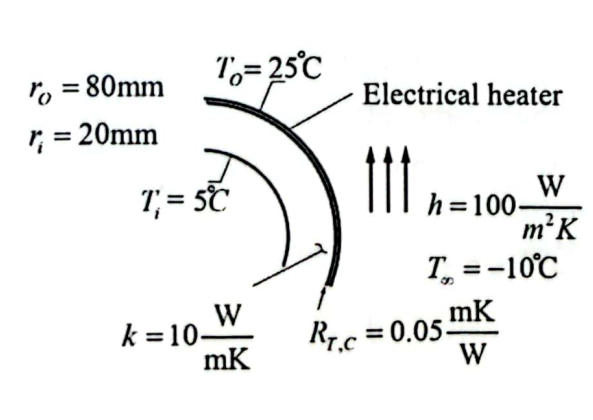
סכמת המערכת.

נתונים:

תרשים נגדים.

לפי התנגדות להולכה, הסעה ומגע, ההתנגדות משמאל למחמם:

מימין:

ולכן הספק החום ליחידת מטר אל הצינור הוא:

סעיף ד’

נתונים:

נחשב תכונות זורם לפי טמפרטורה ממוצעת :

לפי משוואה (IH8.45b) (קראו הערה):

מאחר ופני החלק החיצוני של הצינור רותחים בלחץ אטמוספירי, נסיק כי . בנוסף, מבחינת ההתנגדות, ניקח בחשבון רק את ההתנגדות להסעה הפנימית:

נציב בחזרה ב-(1.2):

נותר לנו רק למצוא את . ריינולדס לפי משוואה (IH8.6):

נסיק שאנו בזרימה טורבולנטית. נניח שאנו בזרימה מפותחת. לפי משוואה (IH8.60), ומאחר והמים מתחממים:

נציב בחזרה ב-(1.3) ונקבל:

נשים לב שמתקיים ולכן אנו באמת בזרימה מפותחת.

סעיף ה’

סכמת הבעיה.

נסמן את הגבולות העליונים:

והגבול הימני:

לפי חוק פורייה, הספק החום ליחידת עומק דרך חתך במיקום הוא:

נבודד את :

אינטגרל מסוים:

נוכל לסדר ולרשום:

נציב גם את תנאי השפה השני:

נציב בחזרה ב-(1.4):

נציב ערכים:

הערה:

אין לי מול מה להשוות את התוצאה הזאת.

סעיף ו’

נתונים:

לפי משוואה (IH11.6b) ומשוואה-(IH11.7b):

נבודד את :

נוכל להניח קיבול חום אחיד:

נציב ערכים ונקבל:

שאלה 2

סכמת הכדור.

נתונים:

סעיף א’

תרשים נגדים.

נחשב את כל אחד מההתנגדויות לפי התנגדות להולכה והסעה, ספציפית בקליפה כדורית.

מאחר ומדובר במצב מתמיד, לפי חוק ראשון, מאחר ו- :

באותו אופן עבור כל אחד מהטמפרטורות:

נשים לב ש- , ונוכל לחשב את כל אחד מהטמפרטורות:

סעיף ב’

נתון:

נניח כי:

1. מדובר במצב מתמיד.
2. ההולכה חד-ממדית, בכיוון הרדיאלי.
3. ייצור החום של הריאקטור לא מתחרש על המעטפת עצמה, כך שאין ייצור חום פנימי בתחום הרלוונטי.

לפי משוואת ההולכה, כאשר נשים לב שהפעם לא קבוע, כך שנצטרך להשתמש בגרסה היותר כללית שלו:

לאחר אינטגרציה:

זוהי משוואה פרידה:

קיבלנו משוואה סתומה. את ו- נוכל למצוא מתנאי שפה.
תנאי שפה על הטמפרטורה ב-:

לגבי תנאי השפה השני, נשים לב שההולכה ב-:

מאחר ו-, על השפה הפנימית של מעטפת הניקל מתקיים:

כך שנוכל לרשום את תנאי השפה על נגזרת הטמפרטורה (חוק פורייה בצורה הבאה):

מהמד”ר (2.1) ותנאי השפה (2.2) ו-(2.3) ניתן למצוא ביטוי ל-.

סעיף ג’

נתונים:

בהנחה והגענו למצב מתמיד לפני הפירוק, נוכל לומר כי ברגע (פירוק המעטפת):

נבדוק מודל חום מקובץ:

לכן נוכל להשתמש במשוואה (IH5.8):

כאשר קבוע הזמן הוא , ו- . כדי לדעת כמה זמן ייקח לליבה לאבד מהאנרגיה האגורה בה:

כבר הראנו ש- בסעיף קודם. נציב ערכים ונקבל:

נוכל לחזור כעת למצוא את בעזרת משוואה (IH5.6):

נציב ערכים ונקבל:

שאלה 3

סכמת הצינור.

נתונים:

סעיף א’

מאחר ומשטח הוא משטח המבודד מצד אחד, נוכל להניח כי , כך שתרשים הנגדים ייראה מהצור הבאה:

תרשים נגדים.

מבחינת ערכי הנגדים, נמצא קודם את מקדמי הראייה. מאחר ומשטח פונה רק כלפי חוץ, . נסיק מסימטריית הבעיה שגם:

מיחס ההדדיות:

כדי למצוא את , נסגור את כדי ליצור משטח פיקטיבי:

משטח פיקטיבי .

מאחר ומשטח ישר, מתקיים . מכלל הסכימה:

מיחס ההדדיות:

לכן מכלל הסכימה:

נחזור למערכת המקורית, ונפעיל שוב את כלל הסכימה:

נציב ערכים ונקבל:

נוכל כעת לחשב את כל הנגדים הרלוונטיים:

סעיף ב’

מהתרשים:

מפתרון מערכת משוואות זה נקבל:

נוכל כעת לחשב את :

סעיף ג’

נתונים:

לפי משוואה (IH1.12e):

מסעיף קודם אנו יודעים שהמעבר חום בקרינה לצינור הוא , ולכן, מחוק ראשון על מעטפת הצינור:

נציב ערכים ונקבל:

סעיף ד’

במקרה המתואר, מקדם מעבר החום הכללי הוא פשוט:

ולכן:

כך שאת משוואה (IH8.45a):

נוכל גם לרשום באופן הבא:

נציב ערכים ונקבל:

סעיף ה’

לפי שיקולים תרמיים בזרימה פנימית:

טמפרטורה ממוצעת (אדום), מקסימלית (כחול), ומינימלית (ירוק) בחתך הצינור.