MCS1_004 Side Pull-In

← Previous: MCS1_003Next: MCS1_005 →

משפעל מקבילי כפול

כפי שראינו בהרצאה הראשונה, לפי משוואה (1.14):

נקרא לדרגת החופש כי ככה רשום בסיכומים של אילתה (הסיבה תבוא בהמשך):

לאחר נרמול (והתעלמות מהמטען הקבוע ):

כאשר:

נשרטט את עבור ערכי שונים (דיאגרמת קווי גובה של ):

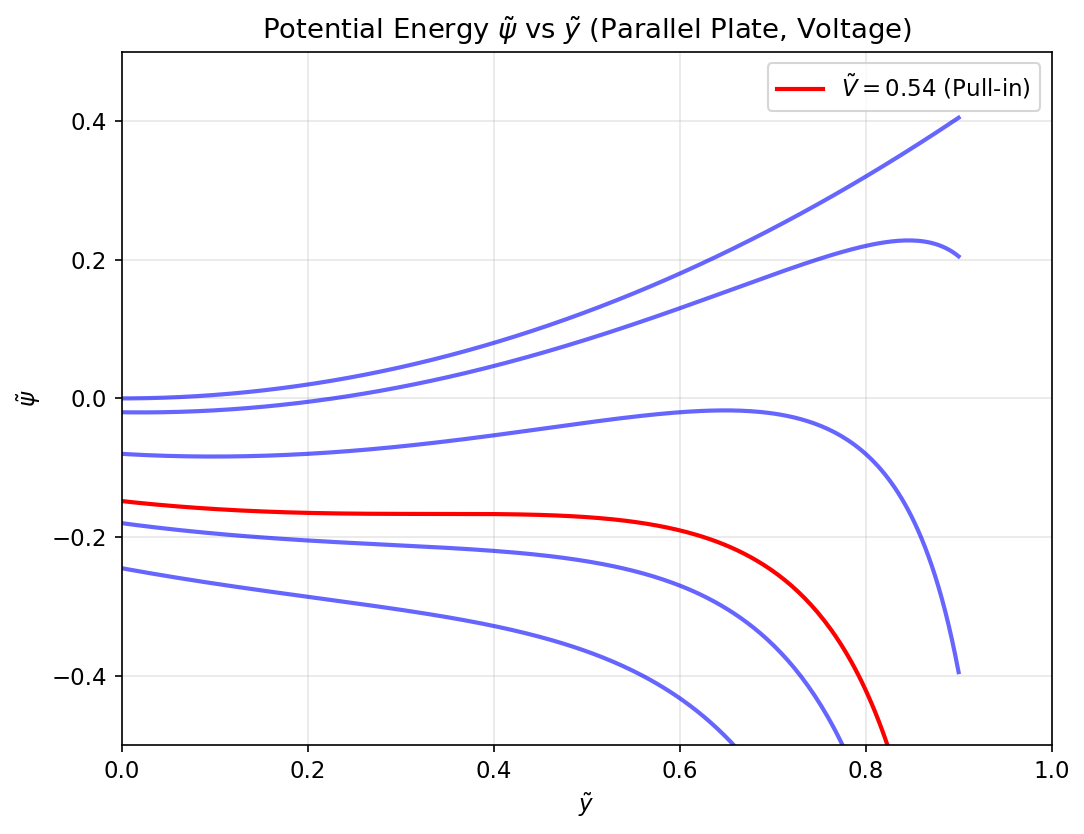
איור 4.1: אנרגיה פוטנציאלית כתלות בהעתק עבור מתחים שונים במפעיל לוחות מקביליים.

עבור ערכי שונים, אנו מצפים לקבל התנהגות שיווי משקל שונה. למשל, עבור (העקומה הכי עליונה), אנו רואים שהעקומה קמורה כלפי מעלה, כך שהיא יציבה ב-. זוהי ההתנהגות הצפויה כי כאשר רק הקפיץ המכני משפיע על מצב המערכת, ואכן הוא יציב כאשר הוא רפוי.
ככל ש- גדל, אנו מקבלים עוד נקודת שיווי משקל לא יציבה בערכים גדולים של , כי בגדלים אלו האלקטרודה הצפה קרובה מספיק לאלקטרודה המוארקת כדי להתגבר על הכוח המכני של הקפיץ.
עבור , נקודת שיווי משקל זו הופכת לאדישה (העקומה האדומה), כפי שראינו בהפעלת מתח.

הכוח הריאקטיבי הוא:

שיווי משקל מתקבל כאשר הכוח הריאקטיבי מתאפס:

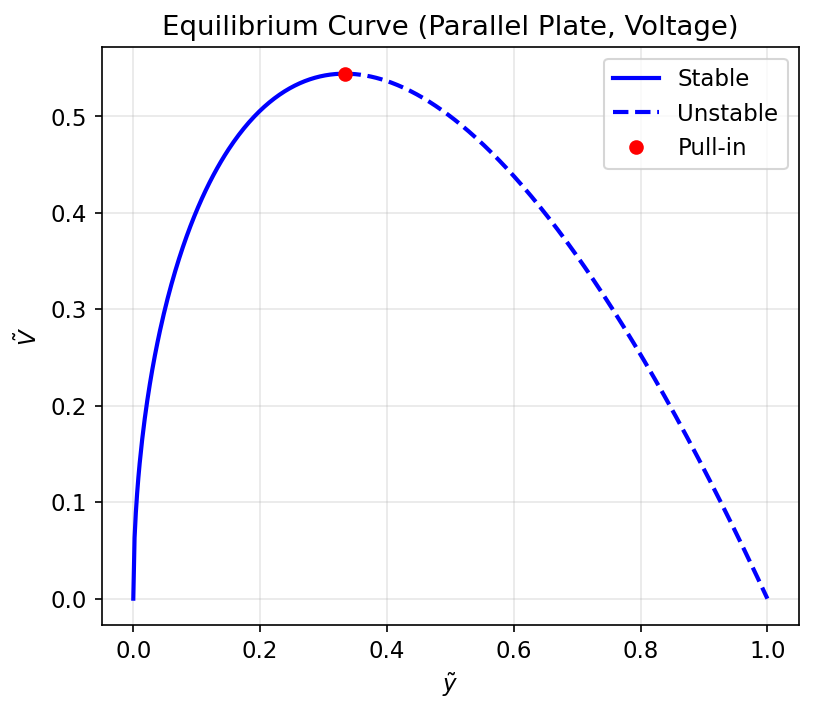
איור 4.2: עקומת שיווי משקל של מפעיל לוחות מקביליים.

הקשיחות:

הקשיחות בשיווי משקל:

הפעלת מתח

נביט כעת במערכת של משפעל מקבילי כפול וסימטרי:

איור 4.3: משפעל מקבילי כפול סימטרי עם כדרגת חופש.

מערכת זו סימטרית (אנו מניחים שאין כבידה) ולפיכך נצפה שעבור כל מתח , הפלטה האמצעית תהיה בשיווי משקל במרכז ().

הקיבול של המערכת (שני קבלים מחוברים ב-מקביל):

ולכן:

ולכן האנרגיה הפוטנציאלית:

לאחר נרמול:

כאשר:

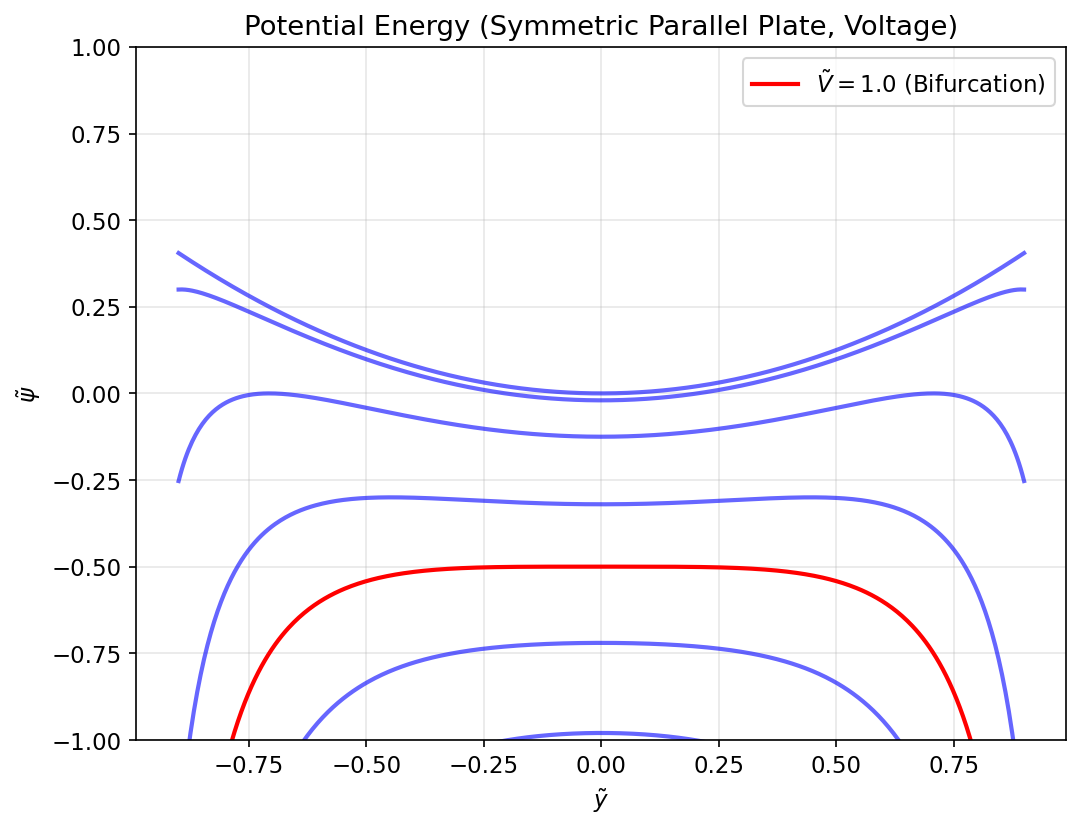
איור 4.4: אנרגיה פוטנציאלית כתלות בהעתק עבור מתחים שונים במפעיל לוחות מקביליים סימטרי.

דיאגרמה זו היא למעשה השלמת מראה של איור 4.1. אנו רואים שמ-, כבר נהיית לא יציבה, ואנו מגיעים למצב של ביפורקציה - אי-יציבות שיכולה להוביל לאחד משני מצבים. במקרה שלנו, pull-in לאלקטרודה העליונה או pull-in לאלקטרודה התחתונה.

כוח התגובה הוא:

שיווי משקל יתקבל כאשר:

הפתרונות הפיזיקליים הם:

כיוון שלא יכול להתקיים .

נגזור כדי למצוא את הקשיחות:

הקשיחות בשיווי משקל:

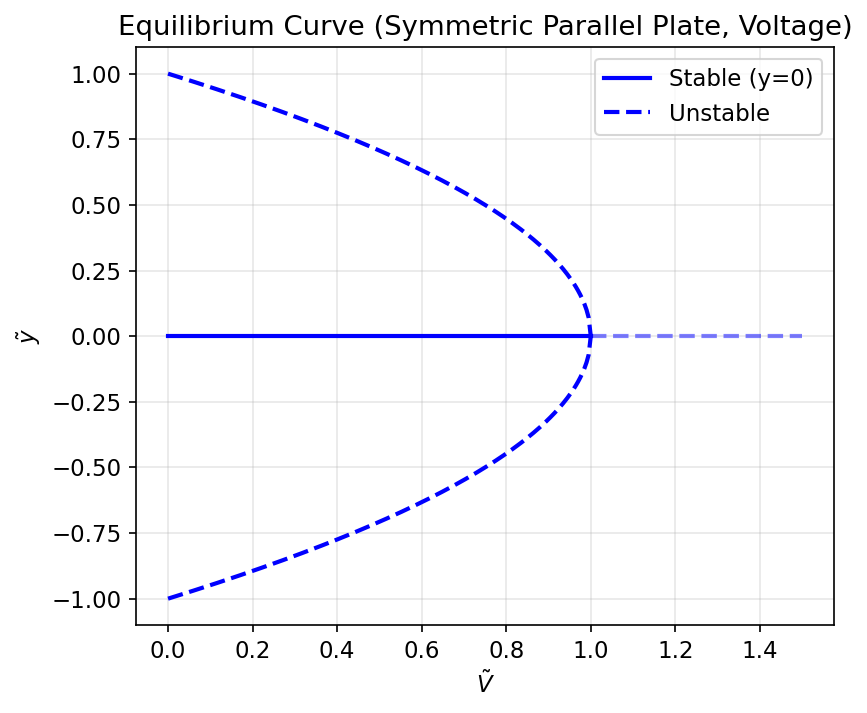
איור 4.5: עקומת שיווי משקל של מפעיל לוחות מקביליים סימטרי.

באיור לעיל ניתן לראות את הביפורקציה - הפיצול לשני מצבי ה pull-in השונים.

הפעלת מטען

בהפעלת מטען, הקבלים עדיין מחוברים במקביל, הרי האלקטרודות הצדדיות מוארקות, והמטען ולפיכך המתח על האלקטרודה האמצעית קבועה.

לכן הקיבול זהה ל-(4.1):

סך האנרגיה הפוטנציאלית:

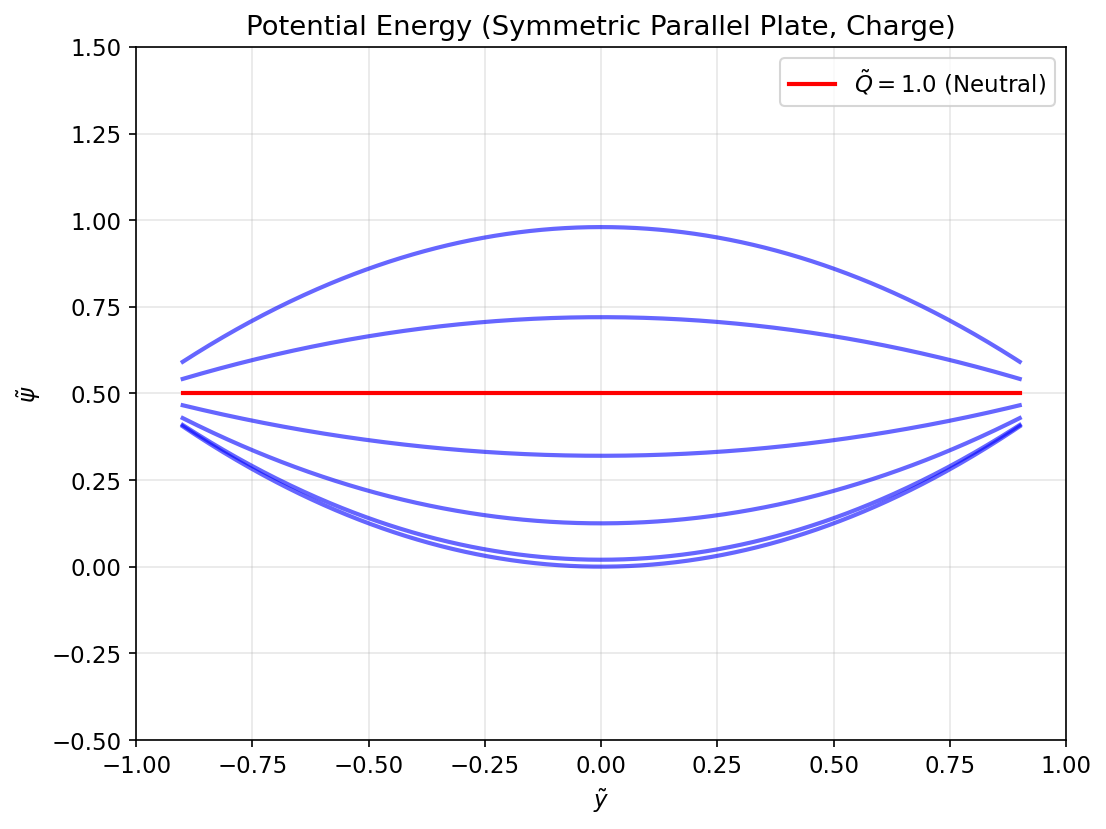
איור 4.6: אנרגיה פוטנציאלית כתלות בהעתק עבור מטענים שונים במפעיל לוחות מקביליים סימטרי.

לאחר נרמול:

כאשר:

הכוח הריאקטיבי:

נקבל שיווי משקל כאשר:

הקשיחות של המערכת:

הקשיחות בשיווי משקל:

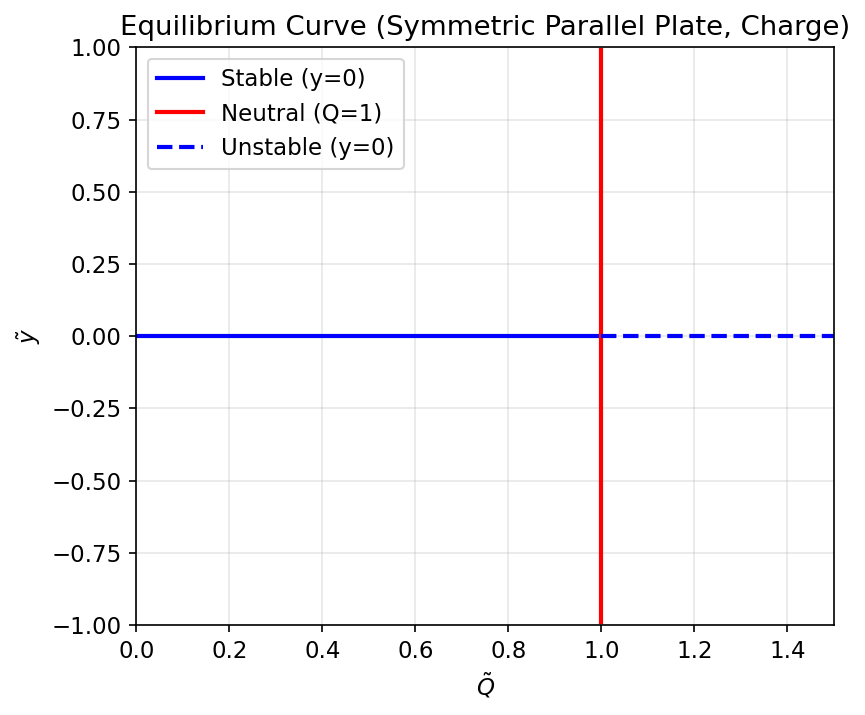
איור 4.7: עקומת שיווי משקל של מפעיל לוחות מקביליים סימטרי בהפעלת מטען.

קיבלנו מערכת שהיא אדישה עבור .

Side Pull In במשפעל מסרק

משפעל מסרק חד-צדדי

נביט כעת מה קורה כאשר במשפעל מסרק ישנה גם דרגת חופש אנכית:

איור 4.8: סכמה של משפעל מסרק חד-צדדי בהתחשבות החופש האנכי.

כעת הקיבול הוא פונקציה של ו-:

לאחר סידור:

כאשר הוא מספר ראשי המסרק על הרוטור (החלק השמאלי המחובר לקפיץ).

כאשר המשפעל מופעל מתח, הפוטנציאל נתון ע”י:

לאחר נרמול:

כאשר:

ו- הוא טווח התנועה הצפוי בכיוון הראשי ().

כוח התגובה:

השיווי משקל של המערכת מתקבל כאשר:

משתי משוואות אלו נסיק שתי פתרונות:

• עבור , משוואה (4.17b) מתקיימת, ומ-(4.17a) נסיק שגם .
• עבור , כדי לקיים את (4.17b) צריך ש: נציב את (4.17a): ולכן:

נסכם:

הפתרונות (4.18a) ו-(4.18b) מוצגים בדיאגרמה הבאה, עבור המקרה המיוחד של ו-:

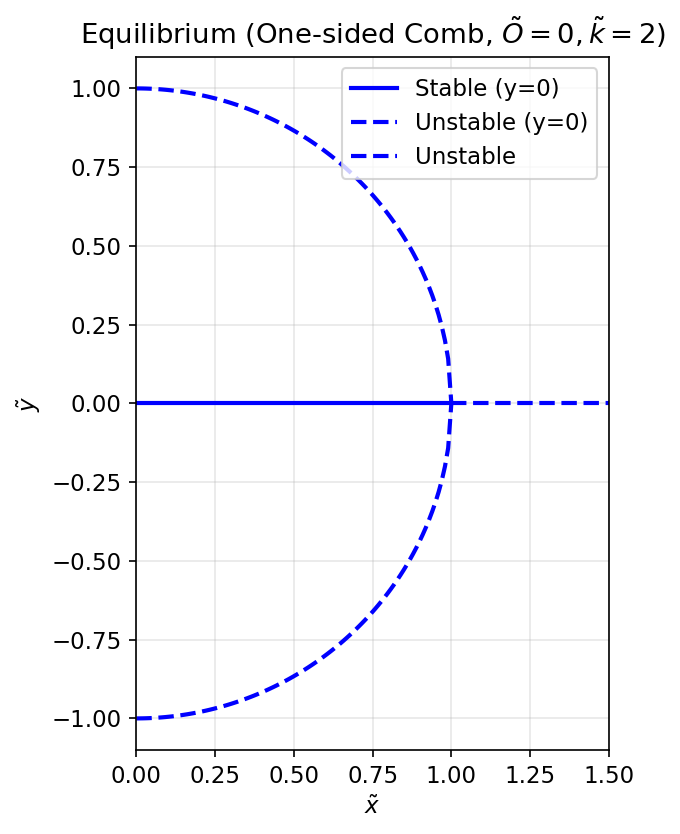
איור 4.9: עקומת שיווי משקל של משפעל מסרק חד-צדדי.

כלל תכן:

טווח תנועה מלא מתקבל ע”י הפעלת מתח , ו-pull in צדדי ניתן למניעה בתוך טווח ע”י קיום .

משפעל מסרק דו-צדדי

במקרה הדו-צדדי:

איור 4.10: סכמה של משפעל מסרק דו-צדדי בהתחשבות החופש האנכי.

סך הפוטנציאל של המערכת הוא:

לאחר סידור:

לאחר נרמול:

כאשר:

ההזזה בכיוון הראשי מוגבלת לטווח כדי להבטיח שהרוטור לא יתנתק מהסטטור.

הכוחות הריאקטיביים:

שיווי משקל:

משתי משוואות אלו נסיק שתי פתרונות:

• עבור , משוואה (4.22b) מתקיימת, ומ-(4.22a) נסיק שגם .
• עבור , כדי לקיים את (4.22b) צריך ש: נציב את (4.22a) ונבודד את לקבלת:

נסכם:

לפני שנשרטט את העקומות שיווי משקל של המשפעל, נשים לב שעבור יישום פרקטי של משפעל מסרק כפול נרצה שכאשר ההזזה מקסימלית בכיוון הראשי (), גודל המתח המנורמל הוא יחידה ().

ממשוואה (4.23a) זה אומר שנרצה לעבור ב- . מהצבה של ערך זה ב-(4.23b) נקבל את עקומות שיווי המשקל (הלא יציבות) באיורים הבאים. עקומות אלו חושבו עבור ערכים שונים של פרמטר הקשיחות , והחיתוך בין עקומות אלו והפתרון הראשון (4.23a) (כלומר, הקו ) הם שתי נקודות pull-in. נסיק מכך שטווח פעולה מלא של אפשרי אך ורק אם . עבור ערכין קטנים יותר של , אי-יציבות של ה- side pull-in יגביל את טווח התנועה.

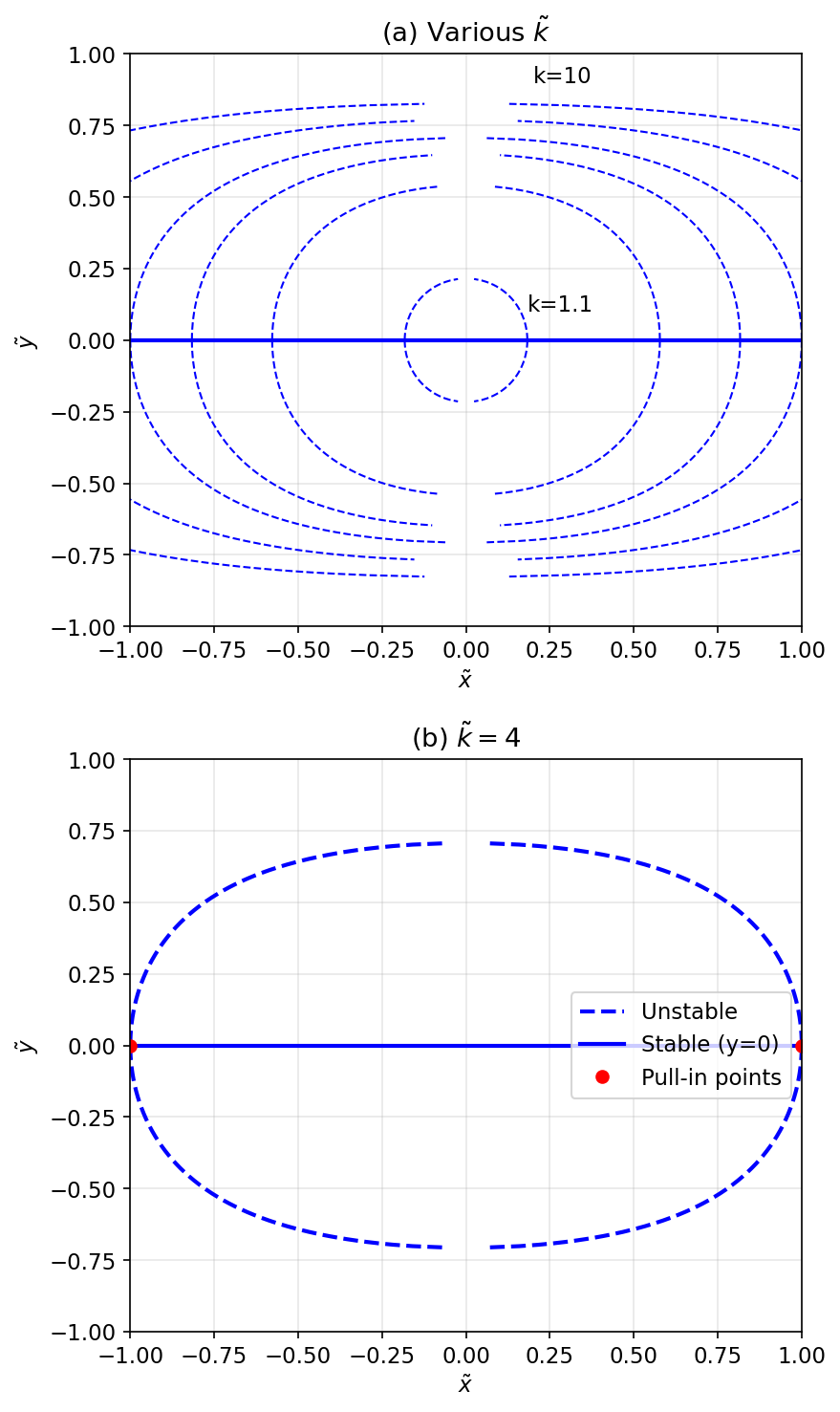
איור 4.11: עקומות שיווי משקל של משפעל מסרק דו-צדדי המציגות מצבי שיווי משקל יציבים (קו רציף) ולא יציבים (קו מקווקו). (א) פתרון משוואה (5) עבור (מהעקומות הפנימיות לחיצוניות). (ב) עקומות שיווי משקל עבור .

פתרונות לטיפול ב- Side Pull-In

הקטע הבא מתבסס על המאמר “Design of Large Deflection Electrostati Actuators” ¹.

בשנות ה-2000, עם העלייה הדרמטית בביקוש להעברת מידע בממדים עצומים, הואצה פריסת תשתיות הסיבים האופטיים ברחבי העולם. בצמתי התקשורת, האותות האופטיים נדרשים להיות מנותבים ליעדם. השיטה המסורתית לביצוע מיתוג זה כרוכה בהמרת האות מאופטי לחשמלי, ביצוע הניתוב האלקטרוני, והמרה חזרה לאות אופטי (O-E-O). תהליך זה הוא יקר, צורך אנרגיה רבה ומהווה צוואר בקבוק בקצבי העברת מידע גבוהים. פתרון יעיל יותר הוא מיתוג אופטי ישיר (All-Optical Switching), המאפשר לנתב את אלומות האור ללא צורך בהמרה חשמלית. מערכות MEMS, ובפרט משפעלים אלקטרוסטטיים המזיזים מראות או חוסמים, מציעות פתרון קומפקטי ויעיל למימוש מתגים אופטיים אלו.

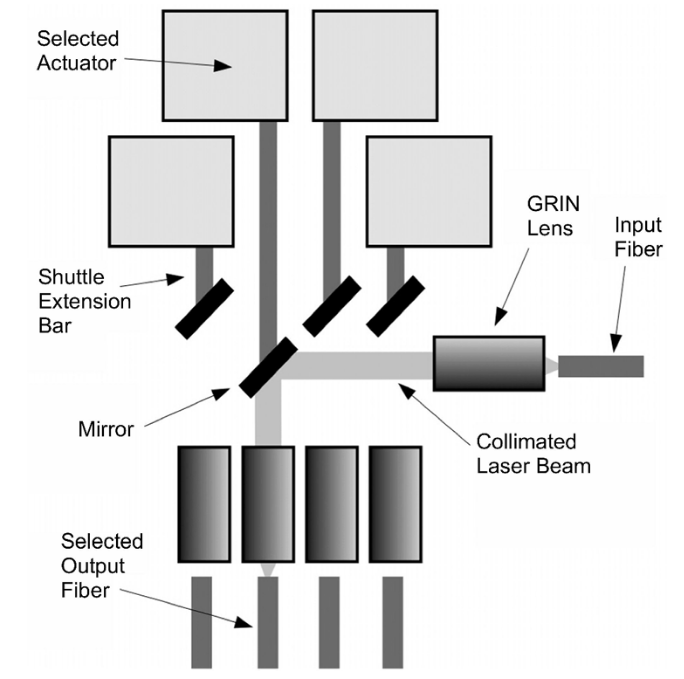
איור 4.12: תרשים סכמטי של מתג אופטי המשתמש במספר משפעלים לינאריים. קרן לייזר, המיושרת ע”י עדשת GRIN, נע שמאלה עד שהיא נחסמת ע”י מראה מוסטת וממוקדת לסיב מוצא ¹.

במאמר פורטו בעיות תכן של side pull-in, ומספר פתרונות עבורן.

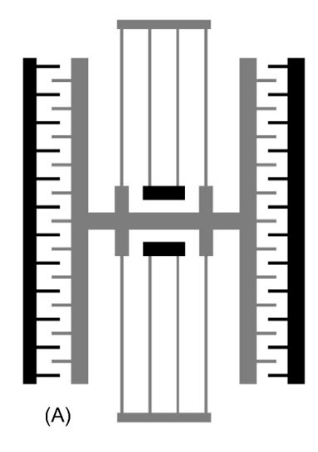
איור 4.13: שרטוט סכמטי של משפעל מסרק מסורתי.¹

במשפעל לעיל, אחת הבעיות האפשריות היא סיבוב של כלל הרוטור - בעיה שמתעצמת ככל שהמסרק גדל בגובהו. בסכמה הבאה, מוצע הפתרון בו העוגנים יוצאים החוצה מהמסרק, והמסרק מתהפך, כך שהרוטור בחוץ והסטטור בפנים. מערך זה הרבה יותר קשיח אנכית, ומאחר והמסרק קרוב יותר לציר הסיבוב, הוא יסתובב פחות:

איור 4.14: שרטוט סכמטי של משפעל מסרק עם חלק נע (shuttle) בצורת U ושני קפיצים מקופלים בלבד.¹

עוד בעיה שעולה היא הקשיחות האנכית של קורות ה-suspension כאשר הן מכופפות. עד כה בחנו את הקשיחות האנכית (צירית) שלהן כאשר הן ישרות, אבל קשיחות זו קטנה בהרבה לאחר הכיפוף שלהן - וכאשר הן מכופפות מדובר בשילוב המקסימלי של המסרק, זהו הרגע הכי קריטי ל- side pull-in!

הפתרון שמציעים במאמר הוא גאוני: נייצר את הקורות מכופפות מלכתחילה בכיוון ההפוך, כך שכאשר מגיעים לשילוב מלא, הקורות ישרות.
בנוסף, מתואר באיור הבא גם פתרון להקטנת כוח ה-side pull-in כתלות בשטח השילוב. אם מקטינים חלק מהשיניים של המסרק (הזווית שרואים בשרטוט) שטח השילוב קטן, ולפיכך כוח ה- side pull-in. למה אז כבר לא לקצר את כל השיניים? כי עדיין חייבים כמה שיניים שיתחילו את תהליך השילוב כדי שבכלל נקבל קיבול אלקטרוסטטי.

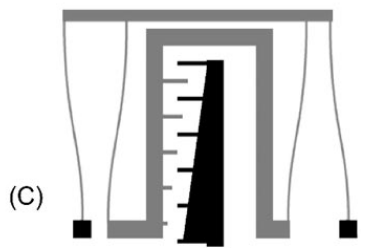
איור 4.15: שרטוט סכמטי של משפעל מסרק משופר, בו הקפיצים ושיני המסרק שונו על מנת לאפשר תזוזות גדולות.¹

איור 4.16: תמונת SEM של משפעל מסרק עם שילוב לינארי של השיניים וקפיצים עם עיקום מוקדם (prebent).¹

איור 4.17: תמונת SEM המראה קפיץ של משפעל עם סדרה של סנפירים בצורת H (etch fins) שנועדו לשלוט בפרופיל דופן הצד (sidewall) מבלי להשפיע על קשיחות הקפיץ.¹

תרגילים

תרגיל 1

שן הרוטור היא בעלת אורך רוחב ועובי , המרחק בין שן סטטור לשן רוטור הוא ואנו מניחים כי הוא אחיד.
מתח מופעל על הרוטור וגורם לתנועה המשנה את שטח החפיפה ההתחלתי בשיעור . בהנחה שהמבנה סימטרי, תופעת ה- side pull-in של שן בודדת, תרחש רק כאשר נגיע לאי-יציבות.

איור 4.18: סכמה של הבעיה הנתונה.

המשתנה קובע את המיקום של הרוטור, בעוד המשתנה הוא משתנה רץ לאורך הקורה שניעזר בו לחישוב השקיעה בקורה. שני המשתנים האלו באותו הכיוון.

נשים לב שניתן להסתכל על הבעיה כקורה רתומה עם עומס מפורס:

איור 4.19: בעיית קורה רתומה עם עומס מפורס לא לאורך כל הקורה.

מבחינת מהמשוואה השולטת בכיוון האנכי, העומס המפורס כתוצאה מהשדה החשמלי נותן לנו את המשוואה הבאה:

התחום הראשון הוא מחוץ לשטח החפיפה לכן לא פועל בתחום זה כוח. התחום השני הוא באזור חפיפת השיניים לכן על השן יש עומס מפורס.

הביטוי לעומס המפורס הינו הכוח הריאקטיבי השקול ליחידת אורך. ניתן לקבל אותו מגזירה הביטוי לאנרגיה האלקטרוסטטית לשן בודדת, לפי דרגת החופש הרלוונטית .

לאחר נרמול:

כאשר:

על סף ה pull-in השקיעה קטנה, לכן ניתן לפתח את הכוח המנורמל באגף ימין לטור טיילור:

אם ניקח קירוב ראשון, המשוואות נהיות הרבה יותר פשוטות:

נפתור את הבעיה בכל אחד מהתחומים. התחום הראשון פשוט ונקבל:

בתחום השני יש לנו מד”ר לינארית עם מקדמים קבועים ולכן הפתרון נתון ע”י פולינום אופייני ושורשיו:

נגדיר כך שנוכל לרשום:

לפיכך הפתרון:

השן רתומה בקצה אחד (לבסיס הרוטור) ובעלת קצה חופשי ב-. לכן תנאי השפה של הבעיה:

בנוסף, יש לנו את תנאי הרציפות בין שני התחומים:

לאחר הצבת תנאי השפה ותנאי הרציפות נקבל בצורה מטריצית את מערכת המשוואות הבאה עבור וקטור המקדמים (כאשר בשל תנאי השפה באפס):

נרצה למצוא פתרון לא טריוויאלי. דרך אחת לעשות זאת לחשב מתי הדטרמיננטה שווה לאפס. במקרה הכי קיצוני בו ישנה חפיפה מלאה בין השיניים ():

לאחר חישוב סימבולי נקבל שהדטרמיננטה מתאפסת כאשר:

מאחר ונרצה פתרון לא טריוויאלי:

שורשי משוואה זו הם למעשה הע”ע העצמיים של הבעיה. נראה את פונקציה זו על הגרף כדי למצוא את השורשים שלה (ישנם אינסוף, אכפת לנו רק מהראשון):

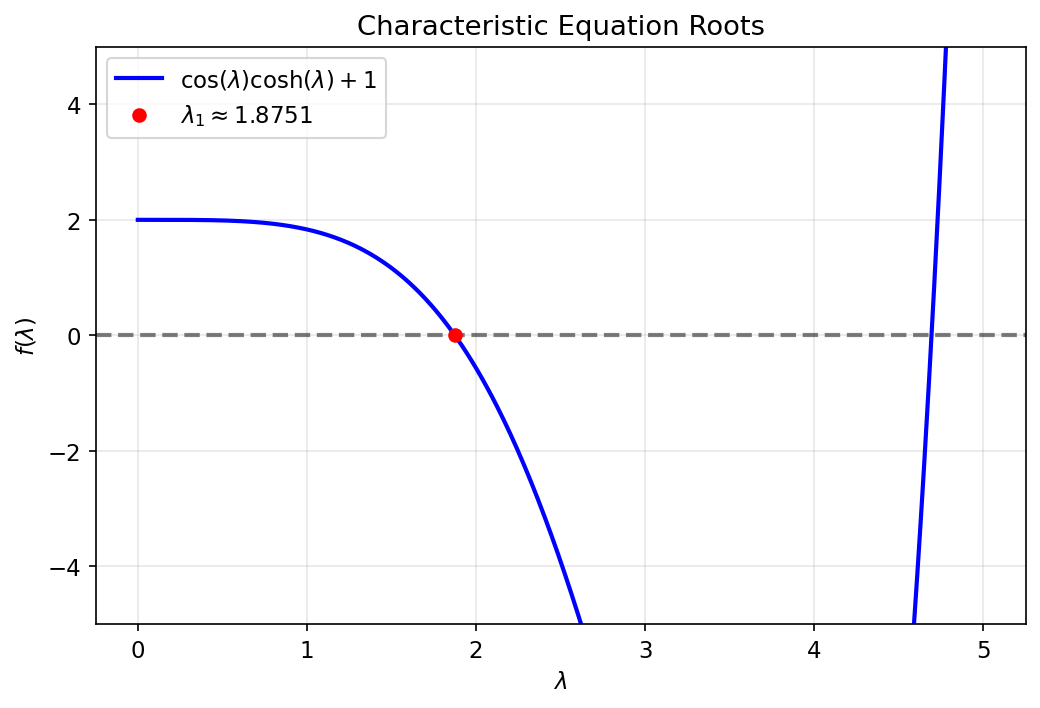
איור 4.20: פתרון גרפי לשורשי המשוואה האופיינית.

השורש הראשון הוא .

ריבועי השורשים (הערכים העצמיים) נותנים לנו את המתח הדרוש על מנת להגיע למצב הביפורקציה - . ניתן לראות כי עבור השורש הראשון שקיבלנו המתח הוא:

אם נסתכל על הביטוי המנורמל למתח שהשתמשנו בו קודם, נרצה לשמור שהמתח לא יגיע למתח ה-pull-in:

בדרך כלל המתח נקבע מתוך דרישות המערכת לתזוזה מסוימת. לאחר שנקבע ערכו של המתח נוכל להשתמש בפרמטר זה כדי לקבל מגבלה על הרוחב :

אם אנו מניחים (כמו במרבית ההתקנים) שמתקיים נקבל

הערות שוליים

1. Grade, J. D., Jerman, H., & Kenny, T. W. (2003). Design of large deflection electrostatic actuators. Journal of Microelectromechanical Systems, 12(3), 335–343. https://doi.org/10.1109/JMEMS.2003.811750] ↩ ↩² ↩³ ↩⁴ ↩⁵ ↩⁶ ↩⁷

← Previous: MCS1_003Next: MCS1_005 →