שדות שוליים
כפי שלמדנו במוצקים 2 ומבוא לחומרים, בקצוות החומר ובפינות חדות אנו עלולים לקבל מאמצים השואפים לאינסוף (אנליטית). מאמצים אלו נובעים מפתרון משוואת לפלס. נוכל לומר אותו הדבר עבור משוואת ההולכה וטמפרטורה. מאחר וגם באלקטרוסטטיקה אנו פותרים את משוואת לפלס:
נסיק שנקבל תופעות דומות למשל במקרה של קבל לוחות מקבילים:
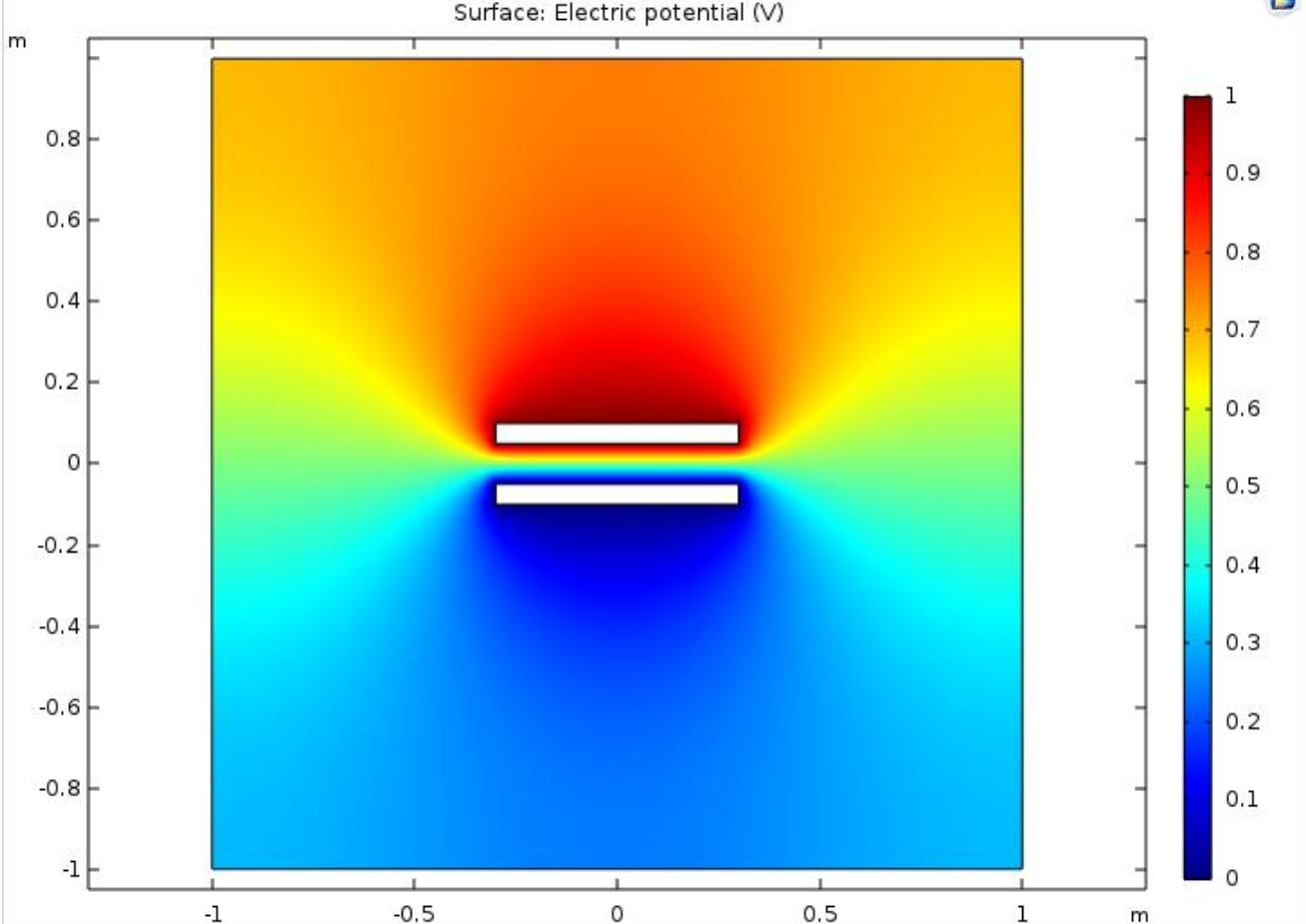
פתרון בעיית קבל לוחות מקבילים באלמנטים סופיים COMSOL. בגרף מוצג הפוטנציאל החשמלי.
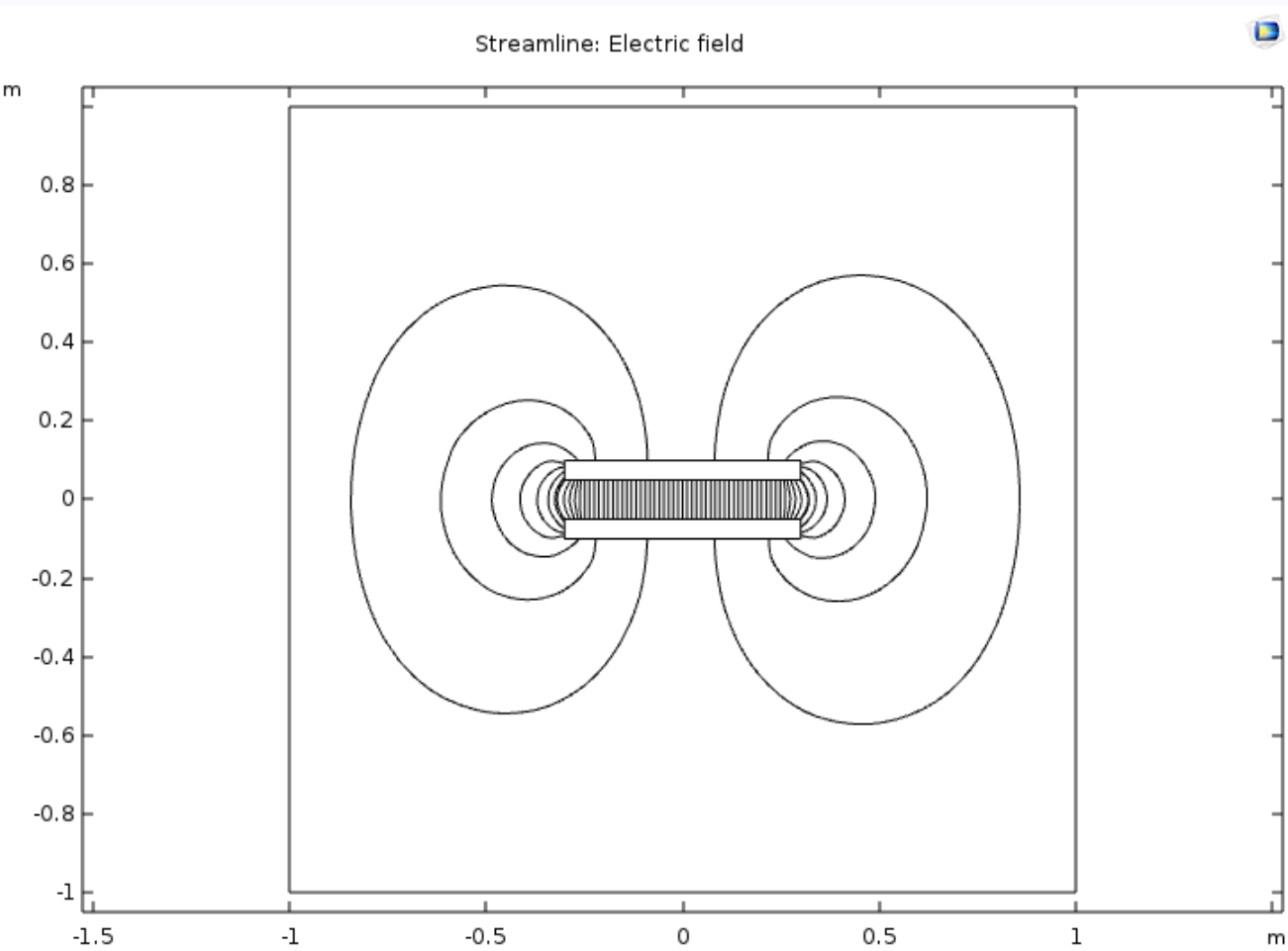
קווי הזרם של השדה החשמלי בפתרון לעיל.
למה המטענים מסתדרים באופן כזה שהוא מתפרס לשוליים?
למה המטענים מתרכזים בצדדים? אם יש כל כך הרבה “מקום” למטענים להתפרס, מדוע הם מתקבצים בשוליים?
הסבר אחד הוא שאנרגטית, מטענים בקצוות יוצרים שדה מגנטי אמנם חזק יותר, אבל משמעותית קטן יותר (מבחינת הנפח שהוא תופס). כלומר, בתצורה שבה המטענים בקצוות, האנרגיה ליחידת נפח במערכת היא מינימלית.
משפעל מסרק
מסרק חד-צדדי
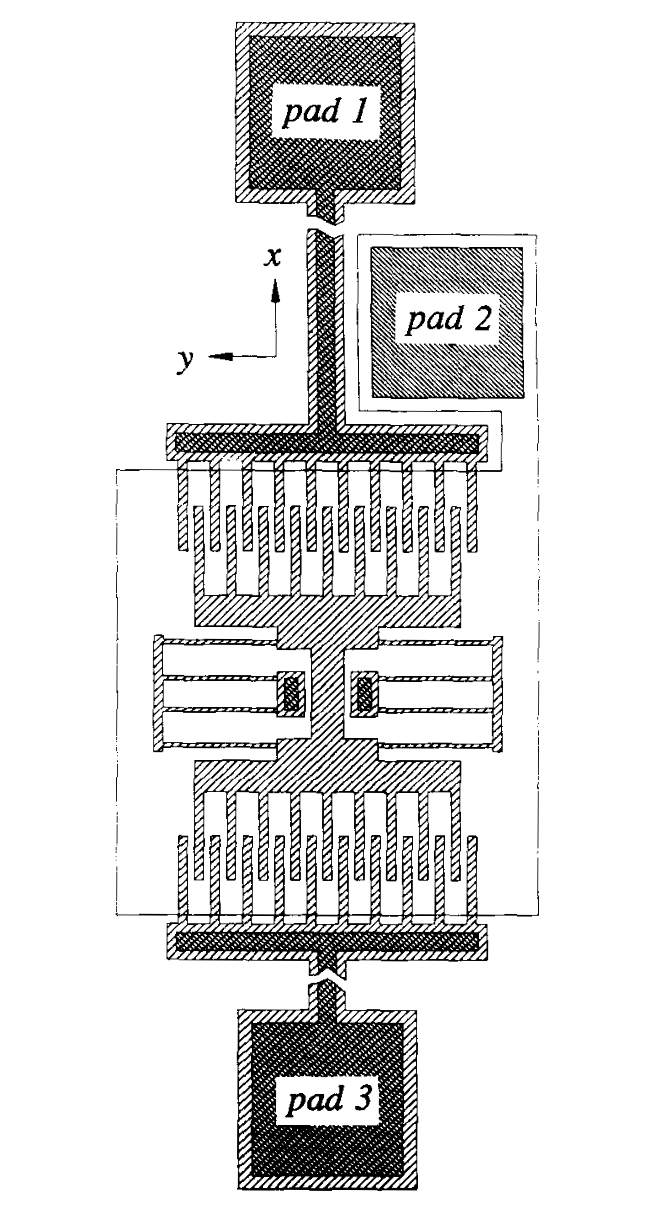
איור 2.1: Layout of a linear resonant plate with comb struchms on both ends and a 50 pn-long folded-beam on each side. (Tang et al., n.d.)
משפעל לוחות מקבילים הוא מערכת שהיא לא לינארית. תכן אלטרנטיבי שמאפשר טווח תנועה גדול יותר הוא comb-drive, הנקרא גם comb actuator.
איור 2.2: סכמה של משפעל מסרק.
במשפעל שתי גאומטריות, כל אחת בצורת מסרק המשלימה זו את זו. צד אחד מחובר לקפיץ לינארי
נשים לב שהקיבול מתרחש אך ורק קרוב לקצוות המסרק - באזור החפיפה ביניהם. בכל שאר האזורים הקיבול זניח - הוא שואף לאפס ככל שמתקרבים לבסיס הפלטות. אמנם עדיין יש קיבול משמעותי קרוב לקצה ראשי הסרגלים (משורטט בסגול מקווקו באיור 2.2) שנסמנו
הקיבול הרלוונטי שנתמקד בו מתרחש בין ראשי המסרק (משורטט בירוק מקווקו באיור 2.2). מאחר ואורך אזור זה הוא
לפיכך, סך הפוטנציאל של המערכת היא:
כאשר
נוכל לחשב את הכוח הריאקטיבי:
תנאי ש”מ:
שימו לב שהכוח המכני לינארי עם
מסרק דו-צדדי
איור 2.3: סכמה של משפעל מסרק דו-צצדי.
במסרק דו-צצדי אנו קוראים למסרק האמצעי הרוטור (ולכן מסמנים את המתח שלו
סך האנרגיה של המערכת:
נקבל:
נגזור לקבלת הכוח הריאקטיבי:
נקבל ש”מ כאשר:
נשים לב שהכוח המכני הוא לינארי עם
תרגילים
שאלה 1
נתון משפעל מסרק חד-צדדי זוויתי:
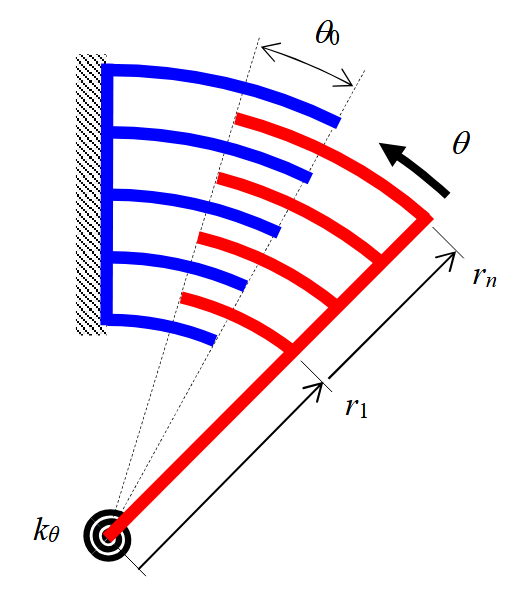
משפעל מסרק חד-צדדי זוויתי.
הזווית הנומינלית של החפיפה בין המסרקים היא
נתחו את תגובת המערכת עבור הפעלת מתח.
פתרון:
האנרגיה הפוטנציאלית היא:
נרצה לחשב כעת את
אמנם האורך של הקבל העליון ארוך יותר מהקבל התחתון, אבל בממוצע האורך של הקבל הוא
אורך הקשת
לפיכך סך הקיבול (שוב, קבלים מחוברים במקביל):
לפי סכום סדרה חשבונית (המרחקים בין כל
ולכן הפוטנציאל:
נגזור כדי למצוא את המומנט הריאקטיבי:
נקבל שיווי משקל כאשר:
ע”מ למצוא את קשיחות המערכת, נגזור לפי
ניתן לראות כי הקשיחות בש”מ קבועה. לכן אין איבוד של יציבות, כלומר אין pull-in.

איור 2.4: Layout of a torsional resonant plate with 4 pairs of balanced concentric comb structures supported by two spirals. (Tang et al., n.d.)
