פנגייה

MCS1_005 חומרים דיאלקטריים

• זמן קריאה: 8 דק'

קבלים דיאלקטריים

דיאלקטרי הוא מבודד חשמלי המסוגל לאגור אנרגיה כאשר מופעל עליו שדה חשמלי. לעומת מוליכים, דיאלקטריים מונעים זרימה של זרם חשמלי כי האלקטרונים שלהם צמודים היטב לגרעין. כאשר מופעל עליהם שדה חשמלי, המטענים השליליים והחיוביים בתוך החומר הדיאלקטרי מוזזים במעט, מה שיוצר שדה חשמלי המתנגד לשדה הקיים.

בחומרים דיאלקטריים, לעומת חומרים מוליכים, ה-תזוזה החשמלית (צפיפות הזרם) מוגדרת כ:

כאשר היא הפרמביליות האלקטרוסטטית בריק, עם יחידות , ו- היא פרמיביליות יחסית - חסרת יחידות.

במובנים של חוק קולון, הכוח שמופעל על מטען סטטי הממוקם ב- ע”י מטען נוסף הממוקם ב- נתון ע”י:

הפרמביליות המוגברת מקטינה את הכוח בין שני המטענים. באותו אופן, הקיבול בין שתי אלקטרודות גדל. הפולריזציה בתוך התווך הדיאלקטרי מקטינה את השדה האלקטרוסטטי האפקטיבי. מאחר והפרש המתח בין האלקטרודות קבוע, המטען חייב לעלות. הקיבול של קבל הממולא בחומר דיאלקטרי עם פרמיביליות יחסית , היא:

חוק גאוס למטען מפורס עם צפיפות , בתוך דיאלקטרי לינארי ואיזוטרופי, על הגבול בין שני דיאלקטריים, הוא:

משימור אנרגיה נסיק כי:

או:

מחוק גאוס (5.4) נסיק כי:

כאשר הוא צפיפות המטען המשטחית על הגבול בין החומרים. אם אין מטען משטחי, אז:

מתגים קבליים

נביט במשפעל מקביל בו האלקטרודה התחתונה מצופה בשכבה דקה של חומר דיאלקטרי בעובי , ופרמביליות יחסית .

איור 5.1: משפעל מקביל עם ציפוי דיאקלטרי.

מאחר ו- הוא גודל רציף, השדה במרחב החופשי הוא , ובדיאלקטרי הוא . המתח בין האלקטרודה העליונה וההארקה נתון ע”י:

נסמן ונוכל לרשום:

המטען על האלקטרודה יהיה:

נציב את (5.8):

נסיק שהקיבול הוא:

נגדיר וגם :

ניתוח של התגובה של המערכת:

נציע נרמול מהצורה:

נקבל:

מאמץ מקסוול

ראינו במשוואה (1.3) שהאנרגיה ליחידת נפח בשדה אלקטרוסטטי נתונה ע”י:

והיחידות שלו הן או . זה אומר שכאשר אנו מעמיסים מרחב מסוים באנרגיה אלקטרוסטטית זה כאילו אנו מפעילים מאמץ.

הגדרת טנזור מאמץ מקסוול היא:

עבור דיאלקטריים עם (כלומר, דיאלקטריים איזוטרופיים):

אז טנזור מקסוול הוא:

עבור המקרה הפשוט של :

מהו הקשר בין מאמץ מקסוול והמאמץ המכני? כאשר למדנו על עיבור תרמי אמרנו שסך העיבור הוא סופרפוזיציה של עיבור שיורי, תרמי, ומכני:

בנוסף, ראינו במוצקים את משוואות שיווי המשקל המוכללות למוצקים אלסטיים:

כאשר הוא סך כוחות הגוף הפועלים על הגוף. נכליל את משוואה זו להכיל גם את מאמץ מקסוול :

בכתיב אינדקסי:

משוואה זו אומרת שאם אין כוחות גוף, סך המאמץ חייב להיות רציף. אם סך המאמץ רציף, אבל מאמץ מקסוול לא רציף, אז יש אי רציפות ב-מאמץ המכני שמפצה עליו.

במכניקה, האי רציפות במאמץ מכני אומרת שחייב להיות כוח מרוכז הפועל על המערכת, אבל כעת כשהכללנו את הקונספט של מאמץ, אי-רציפות במאמץ המכני עשוי להיות כתוצאה מאי-רציפות במאמץ מכני.

נביט בתווך דיאלקטרי בתוך שדה אלקטרוסטטי אחיד:

איור 5.2: תווך דיאלקטרי בתוך שדה אלקטרוסטטי אחיד.

קיבול המערכת הוא (חיבור בטור) הוא:

לאחר סידור והצבת :

כתוצאה מכך, צפיפות המטען לאורך האלקטרודה היא:

מחוק גאוס אנו יודעים שההזזה החשמלית (צפיפות השטף החשמלי) ליד האלקטרודה זהה לצפיפות המטען. נסיק מכך שעוצמת השדה במרווח מחוץ לחומר הדיאלקטרי הוא:

עבור הבעיה החד ממדית הזאת,

מאמץ מקסוול במרווח האוויר ובחומר הדיאלקטרי הוא:

איור 5.3: מיקום המאמצים במערכת.

מרציפות המאמץ הכללי, נסיק:

כלומר, הדיאלקטרי נושא גם מאמץ מכני וגודלו הוא:

לפיכך, החומר הדיאלקטרי נמצא תחת מתיחה.

כפיפת קורות עבים

כאשר אנו דנים בקורות ארוכות ועבות, ישנם מספר סוגים שונים של כיפוף שאנו עלולים לקבל כתוצאה מחומר הקורה ותנאי השפה שמופעלים עליה.

איור 5.4: קורה עבה.

bookhue

איור 5.5: משטחים מונוקלסטיים (או יוניקלסטיים) הם משטחים בעלי עקמומיות אחת, המתאפיינים בכך שהם מתעקמים לכיוון אחד בלבד בכל פעם.

bookhue

איור 5.6: עקמומיות סינקלסטית היא עקמומיות שבה שני כיווני העקמומיות הם מאותו הסימן; מרכזי העקמומיות נמצאים באותו צד של המשטח.

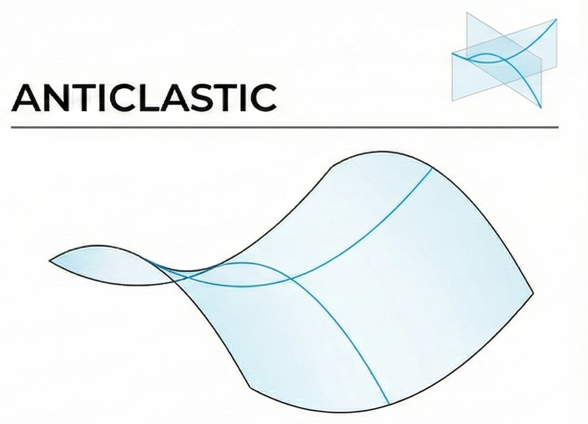
bookhue

איור 5.7: משטחים אנטיקלסטיים הם משטחים שבהם מרכזי העקמומיות נמצאים בצדדים מנוגדים של המשטח.

כפיפה גלילית

עבור כפיפה גלילית (כפיפה מונוקלסטית) של קורה עבה:

בהנחה ו- ו-, נוכל לרשום:

לפיכך, בכפיפה גלילית של קורה עבה, המודול יאנג האפקטיבי הוא:

במציאות, כאשר העקמומיות משמעותית, הפרמטר הרלוונטי הוא

כאשר הוא עקמומיות הקורה. עבור המודול האפקטיבי הוא . עבור המודול האפקטיבי הוא , וביניהם יש מעבר מתון 1.

דוגמה:

הניחו ש- Folded beam suspension עשויה מקורות בגובה , עובי , ואורך .

באיזה עקמומיות נקבל ?
נציב את הגדלים ב-(5.17) ונקבל .

מה תהיה השקיעה?
לפי אויילר-ברנולי לחצי קורה:

בנוסף, אנו יודעים ש:

נציב ונקבל:

באיזה עקמומיות נקבל ?
נציב את הגדלים ונקבל .

מה תהיה השקיעה?
כמו מקודם, רק הפעם נציב :

תרגילים

תרגיל 1

מתוארת הבעיה הבאה:

רוטור דיאלקטרי.

הרוטור עשוי מחומר דיאלקטרי בעל מקדם פרמיטיביות . עובי כל שן הינו , המרווח בין שיניים סמוכות נתון כ- וממד העומק הינו . סה”כ ישנן שיניים ואורך החפיפה ההתחלתי נתון ע”י . על כל שן משיני הסטטור פועלים מתחים קבועים או כך שהפרש הפוטנציאלים בין כל זוג שיני סטטור סמוכות הינו .

נתחיל בלהגדיר את הפוטנציאל של המערכת. מדובר על הפעלת מתח, לכן אנרגיית המערכת, בהתחשב באנרגיית המקור:

יש לנו מבנה מחזורי, לכן ניקח אזור אופייני (מסומן ב- ו- באיור למעלה), נחשב לו קיבול שקול ונסכם. נסתכל ראשית על הקיבול באזור (לא מכיל חומר דיאלקטרי):

אזור מכיל חומר דיאלקטרי, לכן יש לנו שלושה קבלים המחוברים בטור.

נקבל בסוף:

הקיבול הכולל באזור האופייני הינו סכום שני הקיבולים (הפעם חיבור במקביל):

ולכן:

לכן הקיבול הכולל במערכת הינו:

לפיכך:

גישה נוספת לחישוב הקיבול

אפשר לחשב את הקיבול השקול אם מסתכלים על השדה. השדה בחומר הדיאלקטרי הוא ומחוץ לחומר הוא . לכן אם נסתכל על אזור החפיפה, הפוטנציאל החשמלי הוא סכום של השדות כפול רוחב השכבה.

המטען מחוק גאוס:

מאחר ו- , נוכל לרשום:

הקיבול הכולל עבור שן אחת:

לאחר שיש לנו את הביטוי לקיבול הכולל, ניתן להשלים את הביטוי לאנרגיה:

השלב הבא הוא חישוב הכוח הריאקטיבי במערכת:

נוכל לפשט:

הקשיחות תהיה פשוט:

קיבלנו התנהגות שמאוד מזכירה משפעל מסרק סטנדרטי עבור (ראו משוואה (2.2)).

  • ניתן לראות כי קיבלנו כוח אלקטרוסטטי קבוע התלוי ב-ריבוע הפרש המתחים, כמו משפעל מסרק סטנדרטי.
  • בנוסף, כוח זה תמיד חיובי, בדומה למשפעל מסרק רגיל, מכיוון שלפי הגדרה, .

מאחר והמשפעל כל כך דומה למשפעל מסרק סטנדרטי, נשווה בין גודל הכוחות. נזכור כי עבור משפעל מסרק סטנדרטי עם אותם פרמטרים (משוואה (2.1)), הכוח האלקטרוסטטי נתון כ:

נשווה לכוח האלקטרוסטטי שקיבלנו עבור הרוטור הדיאלקטרי:

ניתן לראות כי המכנה גדול מהמונה, בערך בסדר גודל. כלומר הכוח האלקטרוסטטי, במקרה של רוטור דיאלקטרי, קטן יותר תחת אותו הפרש מתחים.

נבדוק רגישות ל- side pull-in. נניח כי הייתה דרגת חופש בכיוון אז הקיבול היה:

ניתן לראות כי הקיבול לא תלוי ב-, ולכן הכוח בכיוון הזה הוא אפס ואיןside pull-in.

הערות שוליים

  1. Kaldor, S. K., & Noyan, I. C. (2002). Differentiating between elastically bent rectangular beams and plates. Applied Physics Letters, 80(13), 2284–2286. https://doi.org/10.1063/1.1459762 ↩

עמודים המציינים את העמוד הזה