פנגייה

SLD2_005 קשרי מאמץ עיבור

• זמן קריאה: 5 דק'

עיבור תלת ממדי

נביט במוט שמורכב מסיבים, תחת מאמץ:

נשים לב שלמרות שיש לנו מאמץ רק בכיוון אחד, לפי תכונות החומר, העיבור יכל לצאת בכיוונים שונים.

נרצה לרשום ביטוי עבור כתלות ב- כמו שעשינו בעיבור עם המודול יאנג, אבל הפעם נרצה להכליל אותו. אנחנו צריכים לקחת בחשבון שלכל מאמץ (נורמלי או גזירה) יכול להיות עיבור שונה בכל אחד מהכיוונים, ויכול גם ליצור הסתובבות של החומר. לכן ה”מודול יאנג” שלנו שונה לכל עיבור שונה:

או בכללי:

הגדרה:

טנזור הקשיחות (Stiffness) הוא טנזור מסדר 4, המוגדר לפי המשוואה הבאה:

למשוואה זו אנו קוראים חוק הוק המוכלל, כאשר הקשר שלה לחוק הוק יוסבר בהמשך.

מאחר והוא טנזור מסדר 4, יש בו רכיבים.
אל דאגה! למרות שיש בו 81 רכיבים, חלקם שווים אחד לשני:

בנוסף, משיקולי אנרגיה, מתקיים .
המסקנה היא שמספר הקבועים הבלתי תלויים יורד ל-21.

לפעמים נהוג להשתמש בטנזור ההפוך, טנזור ההיענות:

הגדרה:

טנזור ההיענות מוגדר כך:

והוא מקיים:

חומר איזוטרופי

הגדרה:

חומר איזוטרופי הוא חומר שאין בו כיוונויות. לא ניתן להבדיל בין דגמים שנלקחו באוריינטציות שונות - כל הדגמים יתנהגו אותו הדבר.

נראה בהמשך כמה תכונות חומר נצטרך כדי להגדיר את הטנזור קשיחות שלו.

חוק הוק המוכלל לחומר איזוטרופי

נביט בחומר הנמצא תחת מאמץ צירי:

ראינו במבוא להנדסת חומרים שניתן למצוא את השפעת המאמץ על העיבור בכיוון הניצב למאמץ - יחס פואסון:

כאשר לא נשכח ש:

משיקולי סימטריה, ניתן להבין שבחומר איזוטרופי הנמצא תחת מאמץ צירי , אין הקטנות בזוויות:

באותו אופן, אם מפעילים רק :

באותו אופן, אם מפעילים רק :

עבור מאמצי גזירה, אם מפעילים רק :

כאשר הוא מודול הגזירה. בעבר הגדרנו אותו כ-, שזה בדיוק אותו הדבר שאנחנו אומרים כאן, כאשר , ו- (עבור ).
book

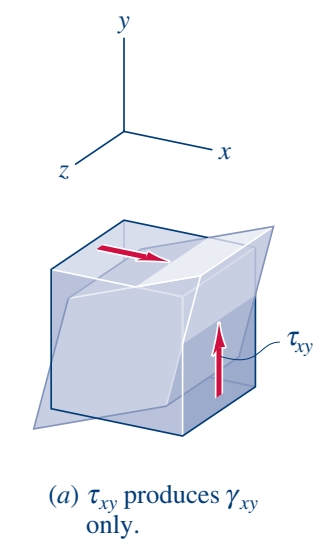
באותו אופן נוכל לעשות עבור .

נרצה להכליל למקרה שבו פועלים כל רכיבי המאמץ :

book

לשלושת הביטויים הראשונים אנו קוראים חוק הוק המוכלל עבור חומר איזוטרופי.

נסיק כי עבור חומר איזוטרופי מספיק לנו 3 תכונות חומר - .

קשר בין המודולים ויחס פואסון

נראה כעת שאפילו בין שלושת תכונות החומר ישנו קשר. נביט למשל במקרה הבא:

טנזור המאמץ שלנו במצב המתואר באיור:

טנזור העיבור שלנו יהיה:

נבצע כעת טרנספורמציה למערכת המסובבת ב-. אנחנו נקבל כי:

וטנזור העיבור החדש:

אנחנו יודעים שחוק הוק חייב להתקיים, בלי קשר לאיזה מערכת צירים אנחנו. לכן:

נקבל כי:

לכן, כדי לתאר את ההתנהגות של חומר איזוטרופי נדרש להגדיר 2 תכונות חומר.

נוכל לרשום מחדש את חוק הוק המוכלל לחומר איזוטרופי:

נוכל גם לרשום את הקשר ההפוך:

נוכל לרשום בצורה אחרת את קשר זה:

כאשר למקדם הוא אחד משני מקדמי למה (Lamé) (המקדם השני הוא מודול הגזירה ), והקשר בין למודול יאנג ויס פואסון נתון ע”י:

הערה:

מצב מאמצים מישורי איננו גורר מצב עיבורים מישורים:

גם ההפך נכון.

מודול נפחי

בעמיסה הידרוסטטית מתקיים:

נרצה למצוא את השינוי הנפח היחסי, כאשר ניעזר בחוק הוק:

נסמן ונקבל כי:

ל- אנחנו קוראים המודול הנפחי (Bulk modulus). ככל ש- יותר גדול עבור מאמץ מסוים, שינוי הנפח היחסי יותר קטן.

גבולות מקדם פואסון

נשים לב שמתקיים תמיד:

לכן, מהקשר בין , נראה כי:

ולכן:

בנוסף, מתקיים:

ולכן:

אז קיבלנו כי בחומר איזוטרופי:

ישנם מבנים מאוד מיוחדים שעבורם , למשל ספירת הוברמן:

תרגיל:
נתון חומר איזוטרופי בעל הקבועים ו-. קבעו האם ההיגדים הבאים נכונים/לא נכונים:

  1. הכיוונים הראשיים של המאמצים והעיבורים בחומר זה זהים.
    פתרון:
    מאחר ומתקיים: אז ההיגד נכון.
  2. מתקיים .
    פתרון:
    לפי הגדרת טנזור ההיענות: טזור העיבור סימטרי, ולכן: נסיק כי: בנוסף, מאינווריאנט: ולכן: לכן הטענה נכונה:
  3. מתקיים .
    פתרון:
    נכון: גם ידוע מחוק הוק המוכלל: כלומר, תלוי רק ב-, ולא ב-, כך שהמקדם שלו לא תורם בכלל:
  4. מתקיים .
    פתרון:
    לפי חוק הוק המוכלל: לפי הגדרת טנזור ההיענות: מהשוואת המקדמים ההיגד לא נכון.
  5. מהו ?
    פתרון:
    לפי הגדרת ההיענות: נקבל:

עמודים המציינים את העמוד הזה