CAL1_008 אינטגרל מסוים

→ קודם: CAL1_007הבא: CAL1_009 ←

האינטגרל המסוים

הקדמה:
בהינתן פונקציה חיובית קטע נרצה להגדיר את השטח בין הגרף של וציר :

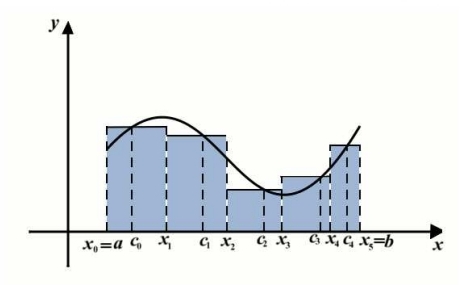
לפי הסימונים בגרף, השטח של כל המלבנים הוא סכומם:

(גובה המלבן נקבע ע”י שנמצא בין שני -ים, והאורך נקבע ע”י המרחק בין שני ה--ים).
ככל שנוסיף עוד -ים, כלומר עוד מלבנים, המלבנים עצמם יהיו יותר צרים, אבל גם ייצגו בצורה מדויקת יותר את השטח מתחת לגרף.

הערות:

1. כאשר הפונקציה שלילית, נגדיר את השטח בינה לבין ציר ה- שלילי.
   נניח כי פונקצייה חסומה ב-. חלוקה של היא:

שנותן תתי קטעים:

נסמן:

ונסמן:

והוא נקרא הפרמטר של החלוקה .
ניקח בחירה של נקודות:

כלומר ניקח איזשהו בין .
נרחיב לעוד:

סכום רימן

הגדרה:

סכום רימן (שהוא סכום המלבנים) המתאים לחלוקה ולבחירת הנקודות הוא:

אינטגרביליות והאינטגרל המסוים

הגדרה:

תהי פונקצייה חסומה ב-. נאמר כי אינטגרבילית ב- אם קיים מספר כך שלכל קיים כך שלכל חלוקה המקיימת ולכל בחירה של נקודות מתקיים:

נסמן:

ערך זה נקרא האינטגרל המסוים של בקטע .

הערות:

1. אם לכל אז לכל חלוקה ולכל בחירה מתאימה של נקודות:

ולכן:

תכונות האינטגרל המסוים

משפט:

1. לינאריות: אם אינטגרביליות ב- אזי גם אינטגריבילית ב- ומתקיים:

ולכן:

(למעשה, גם האינטגרל המסוים הוא ט”ל).
2. אדיטיביות: תהי חסומה ב- ויהי . אינטגרבילית ב- אמ”ם אינטגרבילית בקטעים , ובמקרה זה:

3. אם אינטגרביליות ב- אז גם אינטגרבילית ב-.
4. מונוטוניות: אם אינטגרביליות בקטע וגם לכל אז:

בפרט, אם לכל אז:

בפרט אם לכל אז והוא מוגדר להיות השטח של:

באופן כללי יותר, השטח הכלוא בין הגרפים של שתי פונקציות מעל קטע הוא:

5. אי שוויון המשולש האינטגרלי:
אם אינטגרבילית ב- אז :

לפי סכום רימן:

6. נניח כי מוגדרת ב- פרט למספר סופי של נקודות. נגדיר:

כאשר מוגדרת ב-.
נאמר כי אינטגרבילית ב- ובמקרה זה נגדיר:

למשל:

אז אם נגדיר:

ואז נוכל לומר כי:

תנאים לפונקציה אינטגרבילית

משפט:

1. אם רציפה ב- אז אינטגרבילית ב-.
2. אם חסומה ב- פרט למספר סופי של נקודות, אז אינטגרבילית ב-.
3. אם מונוטונית ב- אז היא אינטגרבילית ב-

רציפות למקוטעין

הגדרה:

נאמר כי רציפה למקוטעין ב- אם קיימות בה מספר סופי של נקודות אי רציפות מסוג סליקה או קפיצה.

המשפט היסודי של החדו”א

פונקצייה צוברת שטח

הגדרה:

תהי מוגדרת בקטע ואינטגרבילית בכל תת קטע חסום וסגור . ניקח ואז לכל נגדיר:

זוהי פונקצייה צוברת שטח.

הערות:

1. אם רציפה בקטע אז היא רציפה בכל ולכן אינטגרבילית ב-.

פונקצייה צוברת שטח רציפה

משפט:

הפונקצייה הצוברת שטח רציפה בקטע .

הוכחה:
למקרה ש-, נוכיח כי רציפות מימין בנקודה .
הפונקציה אינטגרבילית ב- ולכן חסומה בו שאומר שקיים כך ש-) לכל .
יהי :

(לפי אי שוויון המשולש האינטגרלי).

כאשר ב-(1) לפי מונוטוניות האינטגרל.

לכן לפי סנדוויץ’:

שנותן לנו כי:

(כמובן צריך להוכיח גם עבור אבל אין לי כוח).

מסקנה:

תהי פונקציה צוברת שטח. אם פונקציות רציפות בקטע , ונגדיר:

אז רציפה בקטע .

הוכחה:

שני הגורמים שקיבלנו בסוף הם רציפים, הרי רציפה לפי משפט וגם רציפות לפי נתון, כך ש- וגם רציפות כהרכבה של רציפות (לפי משפט. לכן רציפה.

דוגמאות:

1. מתקיים:

המשפט היסודי של החדו”א

משפט:

נניח כי מוגדרת בקטע אינטגרבילית בכל תת קטע חסום וסגור של . יהי ונגדיר לכל :

אם רציפה ב- אז גזירה ב- ומתקיים:

הוכחה:
נוכיח עבור שאינה הקצה הימני של ורק עבור .
יהי . עבור :

• הסבר ל-(1): אדיטיביות
• הסבר ל-(2):
• הסבר ל-(3): לינאריות
• הסבר ל-(4): אי שוויון המשולש האינטגרלי,

מכיוון ש- רציפה ב-, אז קיים כך שכאשר אז

ניקח . אז לכל מתקיים כי:

ולכן .

ולכן:

כאשר ב-(5) לפי מונוטוניות .
לכן, .
באותו אופן, .

לפונקצייה רציפה יש לפונקציה קדומה

מסקנה:

אם רציפה ב- אז יש לה פונקציה קדומה של ב-.
תהי . הפונקציה רציפה בכל נקודה, ולכן לכל .

הכללה של המשפט היסודי

מסקנה:

אם רציפה ב- וגם פונקציות גזירות, אז הפונקצייה:

גזירה ב- ומתקיים :

הוכחה:
ראינו כי אם אז:

נוסחת ניוטון-לייבניץ

משפט:

נוסחת ניוטון-לייבניץ: אם רציפה ב- ו- פונקצייה קדומה של ב- אז:

נהוג גם לסמן:

הוכחה:
נגדיר . רציפה ב-, ולכן, לפי המשפט היסודי, לכל ולכן פונקציות קדומות בקטע ולכן, קיים קבוע כך שלכל מתקיים . בנוסף , וגם .

דוגמאות:

אלגוריתם : אינטגרצייה בחלקים עבור האינטגרל המסוים

נניח כי רציפות. אז:

הערות:

1. אינטגרל לא מסויים:

2. אינטגרל מסויים:

וזה נכון כאשר רציפה. נשים לב כי יש מצבים בהם היא אינה חסומה, ולכן הוא אינו מוגדר.

דוגמאות:

1. עבור:

נסמן:

נציב:

אלגוריתם: שיטת ההצבה באינטגרל מסויים

נניח כי רציפה בקטע ונניח כי גזירה ברציפות (כלומר גזירה וגם רציפה. ומקיימת . אז:

---

הסבר:
נגדיר . לפי המשפט היסודי, לכל .
בנוסף:

אז:

הפונקצייה פונקצייה קדומה של בקטע . לפי ניטון לייבניץ:

דוגמאות:

1. עבור:

נסמן:

ולכן:

תרגילים:

1. חשבו את שטח מעגל היחידה:
   
   פתרון: נגדיר ונחשב: נציב: עבור (1), בתחום האינטגרל ולכן יכלנו להמשיך בלי לפרק.
2. הוכיחו כי אינטגרל של פונקציה אינטגרבילית אי זוגית על קטע סימטרי שווה ל-.
   פתרון:
   מתקיים . נחשב את :
3. חשבו: כי הצבנו: ומתקיים: ולכן אי זוגית.

תרגילים:

1. גזרו את : הפונקציה רציפה, , גזירות ולכן לפי המשפט היסודי:
2. חשבו את הגבול הבא: חשוב להסביר כי מותר להשתמש בלופיטל.
3. הוכיחו כי למשוואה הבאה יש לכל היותר פתרון אחד. נסמן: אז, לפי המשפט היסודי: לפי רול, יש לכל היותר פתרון אחד.
4. הראו כי: קיים במובן הרחב, ומצאו את הגבול, או הראו כי הגבול אינו קיים במובן הרחב.
   פתרון: הגבול קיים במובן הרחב.
   לכל , מתקיים . בנוסף, כאשר . לכן, לכל , מתקיים .
   לפי מונוטוניות של האינטגרל המסוים: לפי גבול של פונקציה|משפט הסנדוויץ’ והפיצה:

→ קודם: CAL1_007הבא: CAL1_009 ←