DVI1_002 רטט חופשי של מערכת בדרגת חופש אחת

→ קודם: DVI1_001הבא: DVI1_003 ←

מבוא

המערכת המכנית הכי בסיסית היא מערכת עם דרגת חופש אחת, שמאופיינת ע”י העבודה שתנועתה מתוארת ע”י קואורדינטה אחת. תנועה זו מתוארת ע”י מד”ר מסדר ראשון - למשל בעזרת חוק שני של ניוטון, נמצא קשר בין הכוח , לתזוזה . במקרה זה אנו קוראים ל- התגובה, ול- העירור (excitation).

הרטט של מערכת כתגובה לתנאי התחלה כלשהם -עירור, נקרא רטט חופשי. כדי למצוא את התגובה לעירורים התחלתיים, אנו צריכים לפתור מד”ר הומוגנית, כלומר אחת עם אפס כוחות מופעלים עליו.
לעומת זאת, הרטט של מערכת כתוצאה מכוחות המופעלים עליו נקרא רטט מאולץ, והוא מייצג בעיה הרבה יותר כללית מהבעיית רטט חופשי, וזאת מכיוון שיש מגוון סוגים שונים של כוחות שיכולים לפעול על המערכת.

• כדאי להסתכל שוב על פונקציות תמסורת ממעלה ראשונה ושנייה.

רטט סביב נקודות שיווי משקל

אנו מכירים מדינמיקה, פיזיקה וכמובן גם ממערכות לינאריות שסביב נקודות שיווי משקל אנו יכולים לפשט משמעותית את משוואות התנועה של מערכת מסוימת.
נביט במערכת הבאה עם דרגת חופש אחת:

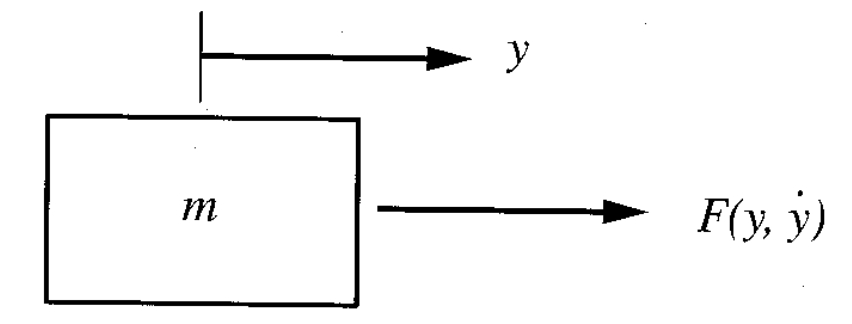
מסה תחת כוח לא-לינארי. (Meirovitch, 2001).

משוואת התנועה של מערכת זו היא מהצורה:

כאשר הוא המסה ו- הוא כוח לא-לינארי כללי שיכל להיות תלוי בתזוזה והמהירות .
אנו מניחים שאין פתרון כללי למשוואה זו, ואנו מעוניינים רק בפתרונות המיוחדים שעשויים לתת תנו תמונה בהירה יותר על התנהגות המערכת. לכן, אנו מחפשים פתרונות למערכת בהם

כיוון שהמהירות והתאוצה הם אפסיים, הפתרונות הקבועים המקיימים את התנאים לעיל מתארים נקודות שיווי משקל. ניתן לקבל אותם ע”י המשוואה:

כאשר מערכת מופרעת מהנקודות שיווי משקל, אנו מסווגים את התנהגותה ליד נקודת שיווי המשקל כיציבה אסימפטוטית, יציבה, או לא-יציבה.

כדי למצוא את סוג היציבות של הנקודת שיווי משקל, נבצע לינאריזציה למערכת - נבחר לרשום את הפתרון של משוואת התנועה באופן הבא:

כאשר היא תזוזה יחסית קטנה מהנקודת שיווי משקל. הנגזרות של פתרון זה:

נפתח טור טיילור ל- סביב הנקודת שיווי משקל :

את כל הביטויים ממעלה שנייה - נבחר להזניח. בנוסף, נבחר את הסימונים:

אנו נקבל משוואה מהצורה הבאה:

זוהי משוואת התנועה החדשה של המערכת תחת הנחות הזזות קטנות. נוכל לסווג את יציבות הנקודות שיווי משקל של מערכת זו ע”י הפרמטרים ו-, ששונים עבור כל נקודת שיווי משקל שונה.
נשים לב שמשוואה זו היא מד”ר עם מקדמים קבועים, כך שפתרונה היא מהצורה:

כאשר הוא קבוע שניתן למצוא מתנאי התחלה ו- הוא קבוע מרוכב. כדי למצוא את נוכל להציב אותו בחזרה במשוואת התנועה החדשה כדי לקבל:

מה שנקרא גם המשוואה האופיינית של המד”ר. פתרונה:

כך שפתרון המד”ר הוא:

נשים לב ש- הם מרוכבים. אופן התנועה בסביבת הנקודת שיווי משקל תלוי בערכים אלו של . תלות זו ניתנת לתיאור ע”י מישור לפלס (נקרא גם מרחב מצב, או מישור-):

יציבות במישור לפלס. (Meirovitch, 2001).

מפתרון המד”ר אנו יכולים לראות שאם הם ממשיים ושליליים, הפתרון שואף לאפס אסימפטוטית.

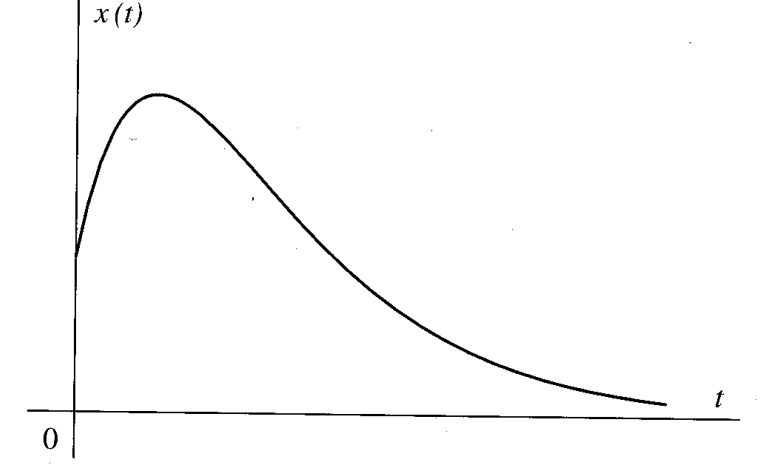
תנועה לא מחזורית דועכת (aperiodically decaying motion). (Meirovitch, 2001).

אם השורשים ו- מרוכבים, הם צמודים אחד לשני, ואז אם החלק הממשי שלהם שלילי, הפתרון גם שואף לאפס אסימפטוטית, אבל הפעם באופן מותנד ככל ש- .

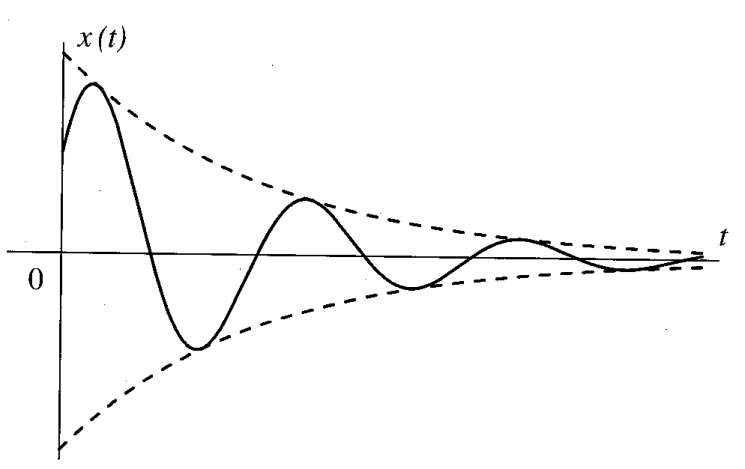
תנועה דועכת באופן מותנד (oscillatory decay motion). (Meirovitch, 2001).

כלומר, נקודת השיווי משקל יציבה אם השורשים נמצאים במישור השמאלי הפתוח של מישור לפלס.

נוכל גם לתאר את יציבות המערכת ישירות ע”י הפרמטרים ו-, דרך מה שנקרא לו המישור הפרמטרי:

יציבות במישור הפרמטרי. (Meirovitch, 2001).

רטט חופשי ללא ריסון

נביט ברטט החופשי של המערכת הלא מרוסנת הבאה:

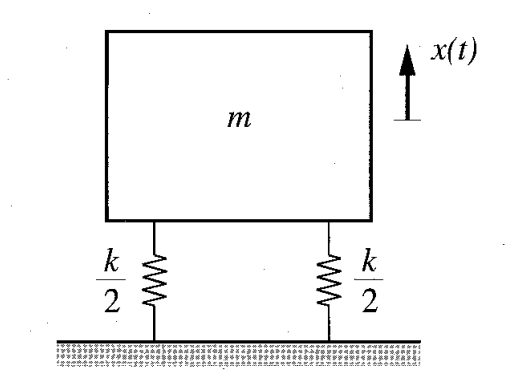
מערכת ללא ריסון וללא כוחות. (Meirovitch, 2001).

משוואת התנועה של מערכת זו היא:

כאשר הוא התזוזה מהנקודת שיווי משקל הסטטית; הוא המסה; ו- הוא קבוע הקפיץ. אם נחלק ב- נקבל את הצורה:

כאשר

הוא קבוע ממשי. הפתרון למשוואה זו תחת התנאי התחלה

הוא אקספוננציאל מהצורה:

אם נציב פתרון זה בחזרה במד”ר, ואז נחלק ב- נקבל את המשוואה האופיינית:

למשוואה זו שתי פתרונות מדומים טהורים:

לכן נוכל לרשום את הפתרון גם בצורה:

כאשר הם קבועי אינטגרציה מרוכבים. מאחר ו- הוא ערך ממשי ו- הוא המצומד של , נסיק ש- הוא המצומד של . אבל, כל מספר מרוכב ניתן לביטוי כהמכפלה של הגודל שלו והאספוננציאל של מספר מדומה. לנוחיות, אנו בוחרים:

כאשר ו- הם קבועים ממשיים. כאשר נציב את בחירות אלו, עם הזהות , אנו מקבלים את התגובה שאנו מכירים למערכת הרמונית פשוטה:

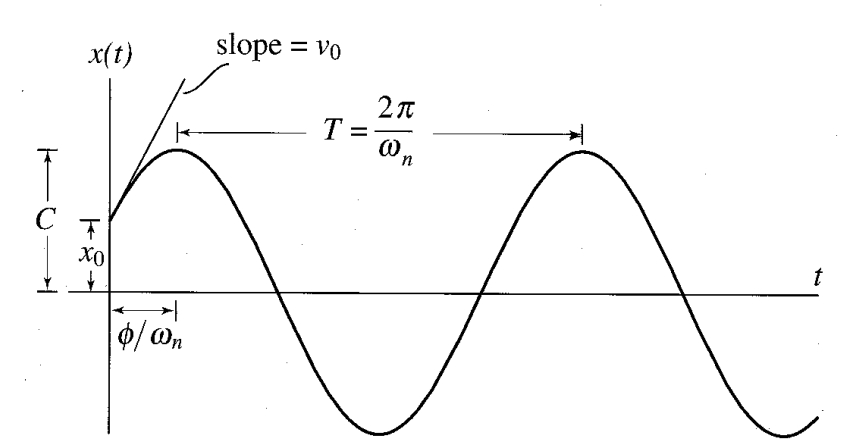
תגובה של מתנד הרמוני לעירור התחלתי. (Meirovitch, 2001).

כאשר נציב את תנאי ההתחלה, נמצא כי:

כך שהפתרון הוא:

רטט חופשי עם ריסון צמיגי

מערכת פשוטה עם ריסון צמיגי מוצגת באיור הבא:

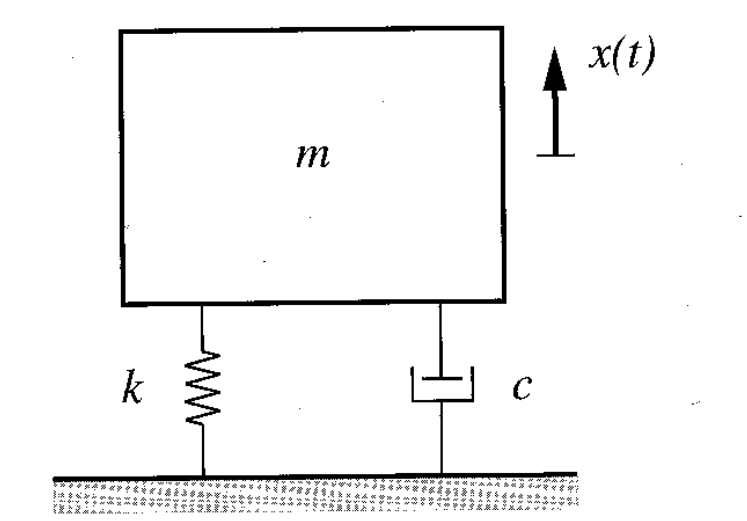
מערכת ללא כוחות, עם ריסון צמיגי. (Meirovitch, 2001).

משיווי משקל נקבל את משוואת התנועה:

כאשר הוא מקדם הריסון הצמיגי. נהוג לחלק ב- כדי לקבל את המשוואה מהצורה:

כאשר הוא התדירות הטבעית של התנודה הלא מרוסנת, ו-

הוא גודל חסר ממד הנקרא מקדם הריסון הצמיגי. הפתרון שלה הוא גם מהצורה:

אבל הפעם:

אופן התנועה סביב נקודת שיווי המשקל של המערכת תלויה בשורשים ו-, שהם בעצמם תלויים בערכי הפרמטר . אנו יכולים להשתמש במישור לפלס (מישור-) כדי לתאר את תלות זו:

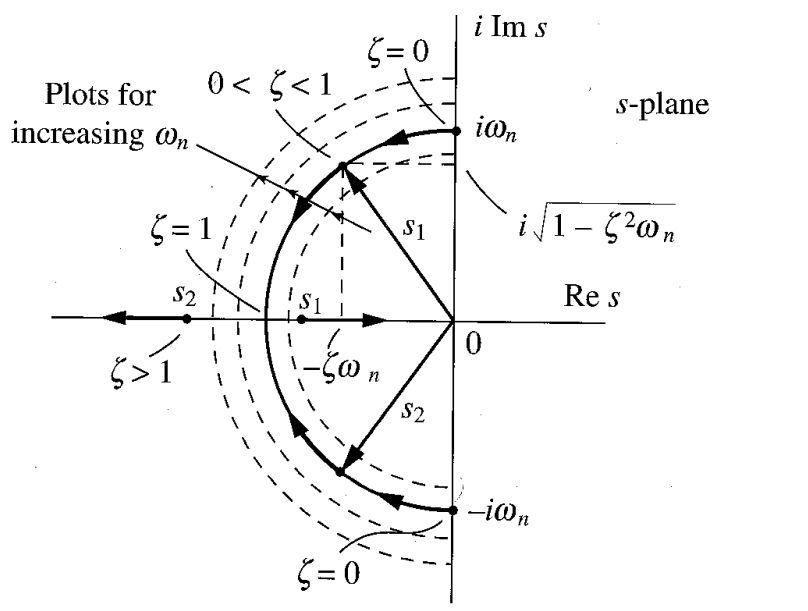
דיאגרמת מג”ש למערכת מרוסנת צמיגית. (Meirovitch, 2001).

נשים לב שמעצם הגדרת , מתקיים , כך שאנו יכולים לצייר את המיקום של השורשים ו- כפונקציות של הפרמטר עבור ערך מסוים של . דיאגרמת מישור- זו נותנת תמונה מלאה לאופן בהם השורשים ו- משתנים עם .

נוכל גם לקשר בין ו-:

מישור פרמטרי למערכת מרוסנת צמיגית. (Meirovitch, 2001).

• עבור , השורשים ו- תואמים לנקודות ו- על הציר המדומה של המישור לפלס, ולכל הציר האופקי של המישור הפרמטרי. מקרה זה מתאר תנודה הרמונית עם תדירות טבעית , כפי שראינו בפרק הקודם.
• עבור , השורשים ו- הם מרוכבים צמודים והם תואמים לזוג הנקודות במישור לפלס שממוקמים באופן סימטרי יחסית לציר הממשי. כאשר משתנה, הזוג נקודות נעים על החצי מעגל בעל רדיוס . נקודות אלו תואמות גם לאזור במישור הפרמטרי בין הציר האופקי לפרבולה . מהאיור לעיל של המישור הפרמטרי אנו יכולים להסיק כי מדובר בדעיכה תנודתית. המקרה של מוכר כתת-ריסון (underdamping).
• עבור , השורשים ו- מתלכדים לנקודה ב- על הציר הממשי של מישור לפלס, והם תואמים לפרבולה במישור הפרמטרי. מקרה זה נקרא ריסון קריטי והתנועה מתארת דעיכה לא-מחזורית.
• לבסוף, עבור , שני השורשים ו- ממוקמים על החלק השלילי של הציר הממשי במישור לפלס, עם בין הנקודה והמקור, ו- משמאל ל-. ככל ש- גדל, נוטה לשאוף ל-, בעוד נוטה לשאוף ל-. מקרה זה תואם לאזור בין הפרבולה והציר האנכי במישור הפרמטרי, ומתואר ע”י דעיכה לא-מחזורית. מקרה זה נקרא ריסון-יתר (overdamping).

עם סיווגים אלו אנו מקבלים תמונה איכותית על אופי המערכת, אבל אם אנו רוצים לקבל תמונה יותר כמותית, עלינו לפתור את המד”ר. אנו יודעים שהפתרון הכללי הוא מהצורה:

כאשר ו- הם קבועי אינטגרציה שנמצא מתנאי ההתחלה:

לאחר פתרון מערכת משוואות זו נקבל ש:

ולכן הפתרון הכללי הוא:

נשים לב מה קורה בכל אחד מהסוגים השונים של הריסון:

• עבור תת-ריסון, , נהוג לרשום את השורשים בצורה הבאה:

  כאשר

  נקרא תדירות הרטט המרוסן, מסיבות שיהיו ברורות בהמשך.
  כאשר נציב את השורשים בפתרון הכללי, וניזכר ש- וגם , נקבל:

  כאשר הוא האמפליטודה ו- הוא הפאזה של התגובה, עם הערכים:

  כדי לשרטט את התגובה של כפונקציה של זמן, נהוג לפרק את הפתרון לשני גורמים, ו-. הגורם מתאר פונקציה דועכת אקספוננציאלית, והגורם הוא פונקציה הרמונית עם אמפליטודה ותדירות (במקום ), מה שמסביר את השם תדירות רטט מרוסן עבור .
  

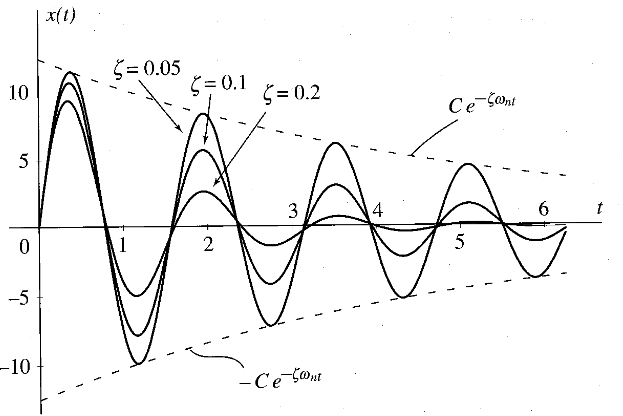
  תגובה של מערכת תת-מרוסנת . (Meirovitch, 2001).

• עבור ריסון-יתר, , השורשים ו- נתונים לפי הביטוי שראינו עבורם במקרה הכללי:

  נשים לב ששני השורשים ממשיים ושליליים. לאחר הצבת שורשים אלו בחזרה בפתרון הכללי, נקבל את הגרף הבא עבור ערכים שונים של :
  

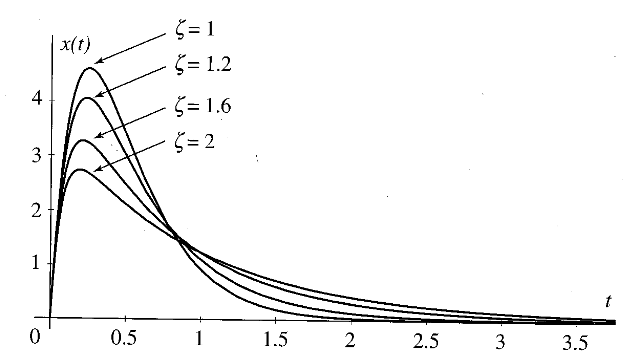
  תגובה של מערכת מרוסנת קריטית () ומרוסנת יתר (). (Meirovitch, 2001).

• במידה והמערכת מרוסנת קריטית, , היא מאופיינת ע”י השורשים:

  במקרה זה, התגובה יכולה להימצא יחסית די בקלות ע”י התמרת לפלס, מה שיוביל אותנו לתגובה:

  שמתאר דעיכה לא-מחזורית. תגובה זו מתוארת גם בגרף לעיל.

שיטת האיזון האנרגטי

בהינתן מערכת עם ריסון שהוא לא בהכרח לינארי, למשל מהצורה:

למרות האי-לינאריות, בעזרת שיטות אנרגיה, נוכל בכל זאת לאפיין את המערכת, בערך. כאשר אנו מביטים ברטט חופשי של המערכות לעיל, אנו רואים שעבור תתי-ריסון אנו מקבלים תגובה סינוסואידית דועכת. הציר האנכי, , מתאר את מיקום המסה, והנגזרת שלו, שהיא המהירות, גם כן סינוסואידית דועכת. נשים לב שהאמפליטודה של המהירות (בריבוע) פרופורציונית לאנרגיה הקינטית של המערכת. כלומר, האנרגיה הקינטית של המערכת דועכת עם הזמן, בפרט בין מחזור למחזור. יותר נכון לומר שהאנרגיה הקינטית והאנרגיה הפוטנציאלית של המערכת קטנים עם הזמן, אחרת המעטפת לא הייתה דועכת. האנרגיה שנעלמת מהמערכת היא כתוצאה מהריסון, שהוא כוח לא משמר. אם נוכל לחשב את העבודה של הכוח המשמר במחזור, נוכל לדעת כמה אנרגיה קינטית ופוטנציאלית איבדנו במחזור, ולפיכך למצוא למשל את מעטפת הדעיכה, אפילו עבור ריסון שהוא לא לינארי. בהמשך, נראה גם איך שיטה זו תעזור לנו למצוא קבוע ריסון לינארי שקול לריסון הלא לינארי .

נשים לב שעם שיטה זו אנו מבצעים מספר הנחות:

• ניתן לקרב את התגובה המרוסנת של המערכת באמצעות פונקציה סינוסואידית:
• תדירות המערכת המרוסנת היא בקירוב תדירות המערכת הלא מרוסנת, .
• אמפליטודת התנודות דועכת לאט - , כאשר הוא זמן מחזור ( עבור period). מה שאומר:

ממאזן אנרגיה בחלקיק, אנו יודעים שהעבודה של כוח לא משמר היא ההפרש בין האנרגיות:

עבור העבודה הלא משמרת שנסמן ( עבור damping), יש לנו רק את הריסון הלא לינארי:

הביטוי בצד ימין הוא במינוס, כי אם נסדר את (2.1) כך שכל הכוחות יהיו בצד ימין, כמו במאזן תנע קווי, כוח הריסון הוא למעשה בכיוון השלילי, שזה הגיוני כי הוא תמיד פועל נגד כיוון התנועה.
נביט בפרק זמן של מחזור, מרגע כללי, ל-:

שאת ביטוי זה שלפנו מההגדרה לעבודה . נקבל:

עבור השינוי באנרגיה, נניח שהזמן כללי שבחרנו הוא בדיוק ברגע שבו אין אנרגיה קינטית, כלומר מהירות המסה היא בדיוק . זה קורה כאשר הגענו לשיא באמפליטודה בתגובה , והאנרגיה הפוטנציאלית גם כן בשיאה. לכן השינוי באנרגיה הכללית של המערכת הוא רק השינוי באנרגיה הפוטנציאלית:

במערכת הנתונה, משוואה (2.1), יש רק קפיץ שיכול לתרום לאנרגיה הפוטנציאלית, כלומר, :

נפתח את האמפליטודה לאחר זמן מחזור בטור טיילור:

הפרש האנרגיות המתקבל:

כאשר הזנחו ביטויים ממעלה שנייה ומעלה.
נציב את (2.4) ו-(2.5) ב-(2.2) ונקבל:

זוהי משוואה דיפרנציאלית שיש לפתור וממנה נקבל קירוב ל-מעטפת התגובה, . דוגמה מפורטת לכן נמצאת בסעיף ד’ בתרגיל 2.

אינטגרלים נפוצים בשיטת איזון האנרגטי

מאינטגרלים אלו ניתן להסיק שעבור ו- :

עבור זמן לא מנורמל, כאשר ו- :

תזוזות קטנות משיווי משקל של מערכת עם דרגת חופש אחת

נביט במערכת עם דרגת חופש אחת, שמשוואת התנועה שלה לאחר לינאריזציה היא מהצורה:

כאשר ו- הם קבועים. נבחר ו- , ונקבל את משוואת המצב:

או, באופן מטריצי:

כאשר הוא וקטור המצב ו-

הוא מטריצת המקדמים. כפי שראינו, אופי התנהגות המערכת סביב נקודת שיווי המשקל תלוי ב- ו-. אנו גם יודעים שפתרון המשוואה הוא מהצורה:

כאשר הוא ע”ע של - מערכות לינאריות. המשוואה האופיינית של היא בדיוק מהצורה של המשוואת תנועה:

והפתרון:

מפירוק מודלי נסיק שהמודלים (חלקי הפתרונות) של המערכת כך ש-

הם:

כאשר ו- הם תנאי ההתחלה של ו- בהתאמה.

במקרים שראינו (מערכת עם דרגת חופש אחת), המערכת הייתה חופשיה - לא פעלו עליה כוחות, כך שלא הייתה אפשרות למערכת להתבדר, והמקדמים חנו רק ברביע הראשון. לפיכך, המקרים הפשוטים שעסקנו בהם כללו רק מערכות יציבות או יציבות אסימפטוטית.

הערה:

הגרפים הבאים מתארים את התנהגות הנקודות שיווי משקל עבור ע”ע שונים במישור- או מישור-, שהינם פשוט טרנספורמציות לינאריות של מישור- שאנו בדרך כלל רגילים אליו. אין צורך להתעמק יותר מדי במה זה או , פשוט הספר מתייחס לזה ככה כי הוא אוהב להיות מדויק בתיאורים הגרפיים שלו. ההבדל היחיד בין האיורים למישור- שאנו מכירים זה שצורת המסלולים אלוי תשתנה, אבל אופי ההתכנסות/התבדרות יישאר זהה.

כדי לאפיין מערכות יותר כלליות, נסווג את כלל האפשרויות של , שמהם ניתן להכליל עוד יותר עבור ערכים עצמיים:

• הע”ע ו- ממשיים ובאותו הסימן:
  המודלים של המערכת הם:

  נוכל לקשור בין ו- כדי לקבל את המשוואה הסתומה:

  שעבור תנאי התחלה ו- שונים נוכל לשרטט אותה באופן הבא (במקרה שבו שני הע”ע העצמיים שליליים):
  

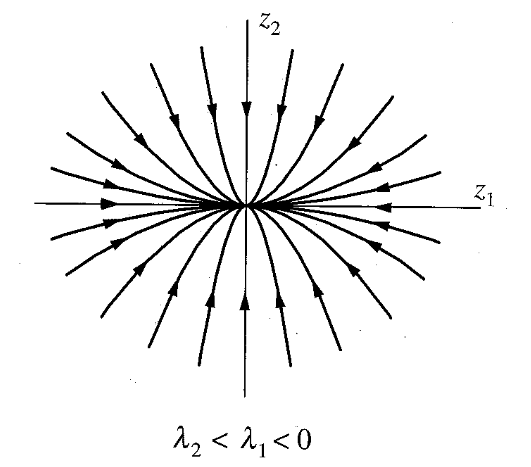
  מסלולים במקרה של צומת יציב. כל מסלול הוא תנאי התחלה שונה - כמו בפתרון כללי למד”ר. (Meirovitch, 2001).

  נקודת השיווי משקל המתוארת לעיל נקראת צומת. מכיוון שהמסלולים שואפים לשיווי משקל כאשר , צומת זה הוא צומת יציב (SN - stable node). מהגדרה, צמתים יציבים הם יציבים אסימפטוטית. במידה ו- ו- חיוביים, ומקיימים , החיצים באיור לעיל פשוט הופכים כיוונים, והנקודה הופכת להיות צומת לא-יציבה (UN - unstable node).

• הע”ע ו- ממשיים ובכיוונים שונים:
  נניח ש- חיובי ו- שלילי. במקרה זה המסלולים מתוארים ע”י

  אם נשרטט אותם עבור תנאי התחלה ו- שונים:
  

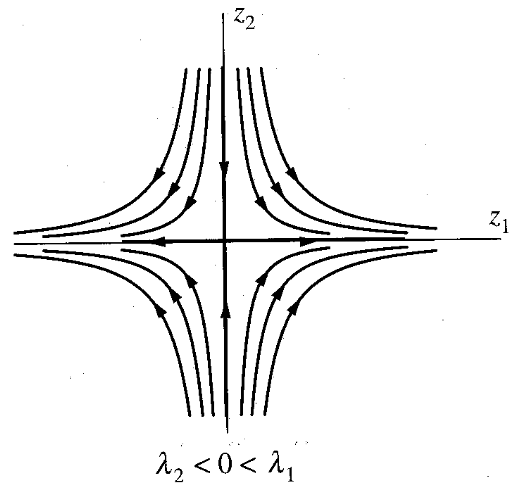
  מסלולים במקרה של נקודת אוכף. (Meirovitch, 2001).

  במקרה זה הנקודה נקראת נקודת אוכף (SP - saddle point), שהיא לא יציבה.

• הע”ע ו- מרוכבים צמודים, :
  בהנחה ונסמן:

  המסלולים יהיו בצורה של ספירלה. עבור , המסלולים מתכנסים לנקודת שיווי משקל, ואילו עבור ו-, המסלולים מתבדרים.
  

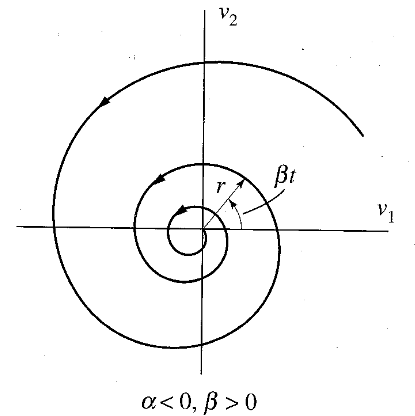
  מסלולים במקרה של פוקוס יציב. (Meirovitch, 2001).

  בשני המקרים, הנקודת שיווי משקל נקראת נקודת ספירלה, או פשוט פוקוס (focus). במקרה הראשון, , הפוקוס הוא יציב אסימפטוטית (SF - stable focus), ובמקרה השני, , הפוקוס לא יציב (UF - unstable focus).

• הע”ע ו- מדומים צמודים, :
  זהו מקרה מיוחד של המקרה הקודם, במקרה בו . אנו נקבל קבוצה של עיגולים שמרכזם בנקודת המשקל. נקודה כזאת נקראת מרכז (C - center), שהיא רק יציבה.
  

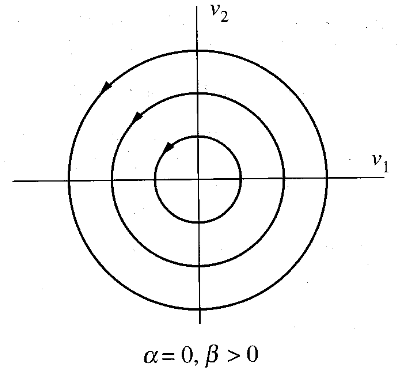
  מסלולים במקרה של פוקוס מרכז. (Meirovitch, 2001).

נוכל לסווג את הסוגים השונים של נקודות שיווי המשקל גם על המישור הפרמטרי:

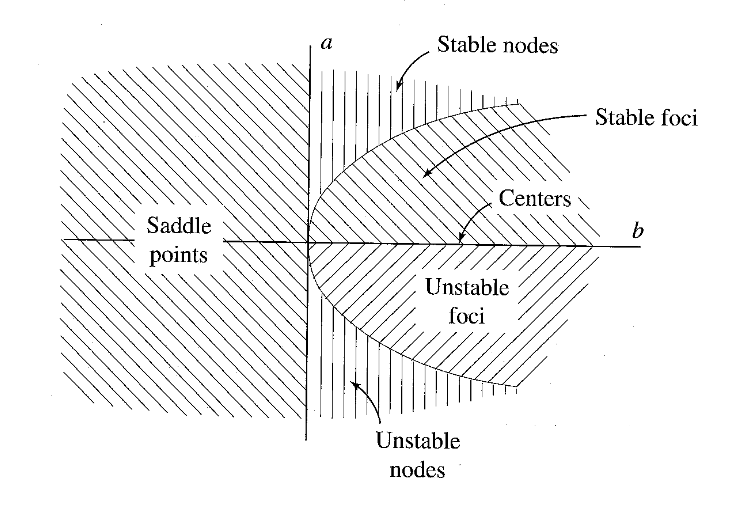
נקודות שיווי משקל במישור הפרמטרי. (Meirovitch, 2001).

ריסון קולון - חיכוך יבש

ריסון קולון מתרחש כאשר גופים מחליקים על מישורים יבשים. כדי שתנועה תחל, חייב להיות כוח הפועל על הגוף שמתגבר על ההתנגדות לתנועה הנוצרת ע”י החיכוך. החיכוך היבש מקביל למשטח ופרופורציונלי לכוח הנורמלי למשטח. במקרה של מסה-קפיץ באיור הבא, הכוח הנורמלי שווה למשקל :

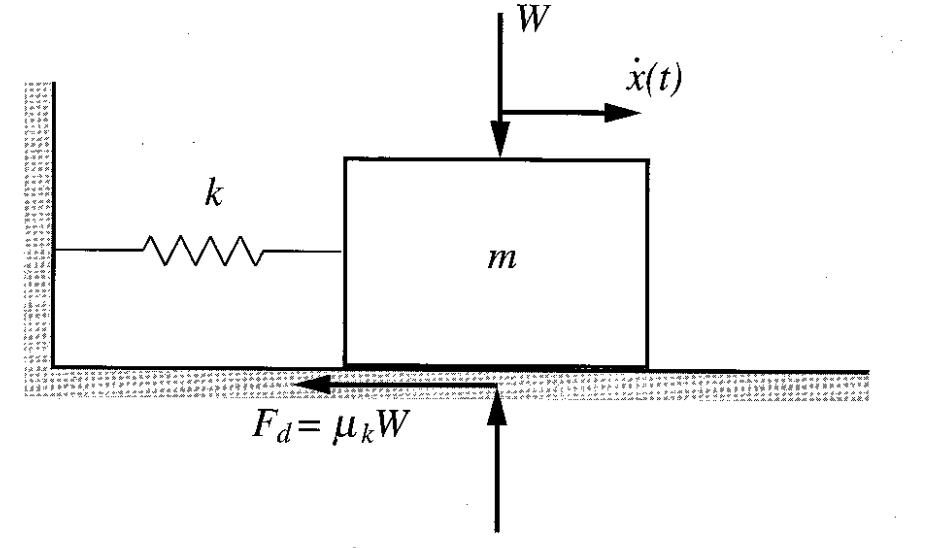
מערכת מסה-קפיץ הנתונה לריסון קולון. (Meirovitch, 2001).

קבוע הפרופורציה הוא מקדם החיכוך הסטטי , מספר שנע בין ו- כתלות בחומרי המשטחים. ברגע שתנועה החלה, הכוח יורד ל-, כאשר הוא מקדם החיכוך הקינטי, שגודלו לרוב קטן מ-.
כיוון כוח החיכוך הוא מנוד בכיוונו למהירות, ונשאר קבוע בגודלו כל עוד הכוחות שפועלים על המסה מספיק גדולים כדי להתגבר על החיכוך היבש. אחרת, התנועה תיפסק.

נסמן ב- את גודל כוח הריסון, כאשר . לכן משוואות התנועה:

כאשר הסימון הוא בעצם ה- signum function, או sign of - פונקציה שיש לה את הגודל אם הערך שניתן לה הוא חיובי והערך אם הוא שלילי.

מתמטית, ניתן לתאר את הפונקציה הזאת כ:

המד”ר שקיבלנו לעיל היא לא לינארית, אבל נוכל להפריד אותה לשתי משוואות לינארית, אחת לערכים חיוביים של ואחת לערכים שליליים של :

הפתרון למשוואות אלו ניתנות למציאה בפרקי זמנים, כל פעם פרק זמן אחד, כתלות בסימן של . ללא פגיעה בכלליות הבעיה, נניח שהתנועה מתחילה ממנוחה עם המסה בנקודה , כאשר ההעתק ההתחלתי גדול מספיק בשביל הקפיץ כדי להתגבר על כוח החיכוך הסטטי. נסיק שהתנועה תהיה מימן לשמאל, והמהירות תהיה שלילית, כך שנפתור את המד”ר עם קודם. נוכל לרשום את מד”ר זו בצורה:

כאשר ו- . הפתרון של מד”ר זה הוא:

שמייצג תנודה הרמונית על תגובה ממוצעת . פתרון זה תקף רק עבור כאשר הוא הזמן בו המהירות יורדת לאפס והתנועה עומדת להתחיל בכיוון השני.
נמשיך כעת לפתור עבור פרק הזמן הבא, עבור ועם התנאי התחלה המתאימים. נקבל ש:

ביחס לפתרון הקודם, האמפליטודה של הגורם ההרמוני קטן יותר ב- והתגובה הממוצעת היא . פתרון זה נכון עבור פרק הזמן .
נוכל להמשיך את תהליך זה, אבל מהר מאוד נמצא תבנית לכל פרקי הזמן. לאורך כל חצי מחזור התנועה מורכבת מגודל קבוע השווה לערך הממוצע של הפתרון ומגורם הרמוני עם תדירות השווה לתדירות הטבעית . הגודל הממוצע של הפתרון מתחלף בין ו-, ובסוך כל חצי מחזור גודל זה קטן ב- . נסיק כי עבור ריסון קולון הדעיכה היא לינארית עם הזמן, לעומת הדעיכה האקספוננציאלית לריסון צמיגי.

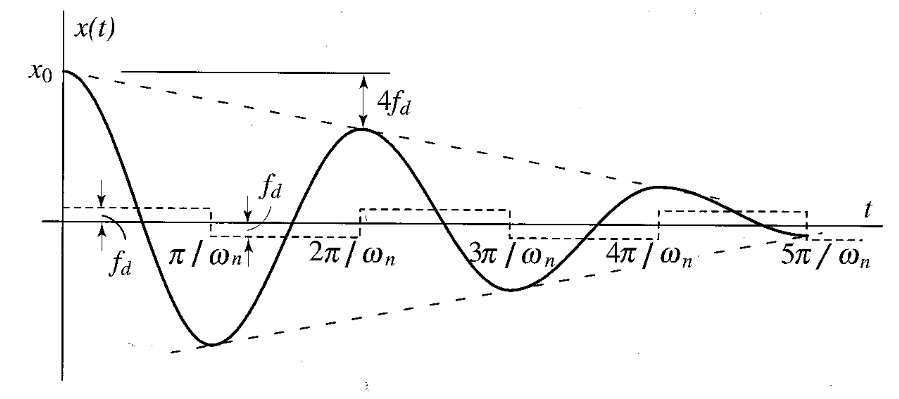
תגובה של מערכת הנתונה לריסון קולון. (Meirovitch, 2001).

התנועה מפסיקה בפתאומיות כאשר ההעתקה בסוף של חצי מחזור לא גבוהה מספיק בשביל הקפיץ כדי להתגבר על החיכוך הסטטי. זה מתרחש בסוף חצי מחזור עבורו האמפליטודה של הגורם ההרמוני קטן יותר מ-. אם נסמן ב- את החצי מחזור לפני הפסקת התנועה, נסיק ש- הוא המספר הקטן ביותר המקיים את אי השוויון:

תרגילים

תרגיל 1

נתון חרוז בעל מסה הנע בחופשיות על גבי חישוק אנכי בעל רדיוס . החישוק מסתובב סביב ציר אנכי במהירות זוויתית קבועה . מיקום החרוז מתואר באמצעות קואורדינטה מוכללת .

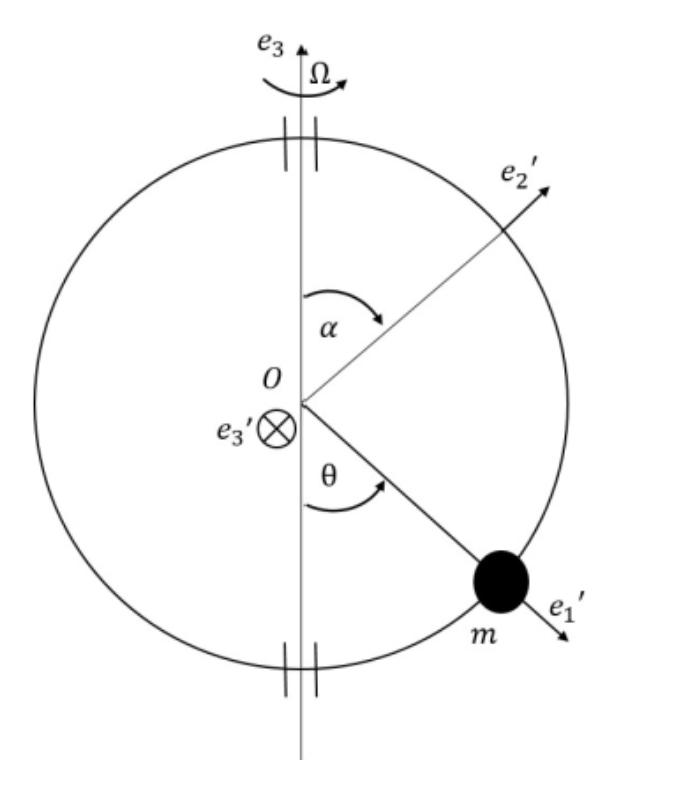
סכימת המערכת

סעיף א’

הרכיבו את משוואות התנועה של המערכת באופן לגראנז’י.

פתרון:
נגדיר מערכת צירים מקומית שראשיתה בציר החישוק ו- בכיוון החרוז. לכן:

נשים לב ש:

ולכן:

המיקום של החרוז:

נגזור לפי כלל האופרטור:

הלגראנז’יאן:

נציב במשוואות לגראנז’:

נקבל את משוואת התנועה:

סעיף ב’

נרמלו את משוואות התנועה.

פתרון:
נגדיר את הגדלים הבאים:

• תדירות עצמית של החרוז בעקבות אילוצי הכבידה ורדיוס הסיבוב:
• הזמן הנדרש להשלמת מחזור אופייני:
• יחס המהירות הזוויתית הכוללת של החרוז לתדירות העצמית שלו: נפתח את משוואת התנועה המנורמלת: נשים לב ש- הוא הנגזרת השנייה של לפי , שאנו מעוניינים לנרמל גם אותו (לפי ). נראה כי: כאשר .
  נציב בחזרה במשוואת התנועה כדי לקבל:

סעיף ג’

חשבו את נקודת שיווי המשקל של המערכת.

פתרון:
נדרוש ש- :

ערכי המקיימים את משוואה זו מהווים את נקודות שיווי המשקל והם:

סעיף ד’

חקרו את יציבות המערכת סביב נקודות שיווי המשקל.

פתרון:
נבטא את משוואת התנועה כמערכת משוואות לא-לינאריות מסדר ראשון. נבחר:

ולכן מערכת המשוואות:

נרצה לבצע לינאריזציה למערכת. נסמן:

היעקוביאן שלו:

ולכן:

כדי לסווג את נקודות שיווי המשקל נרצה למצוא את הע”ע שלהם:

נבחן את יציבות נקודות השיווי משקל:

• אם :
  נקבל ש נפרק למקרים:
• אם , כאשר :
  נקבל ש נשים לב ש- הוא הוא , אבל עבור .

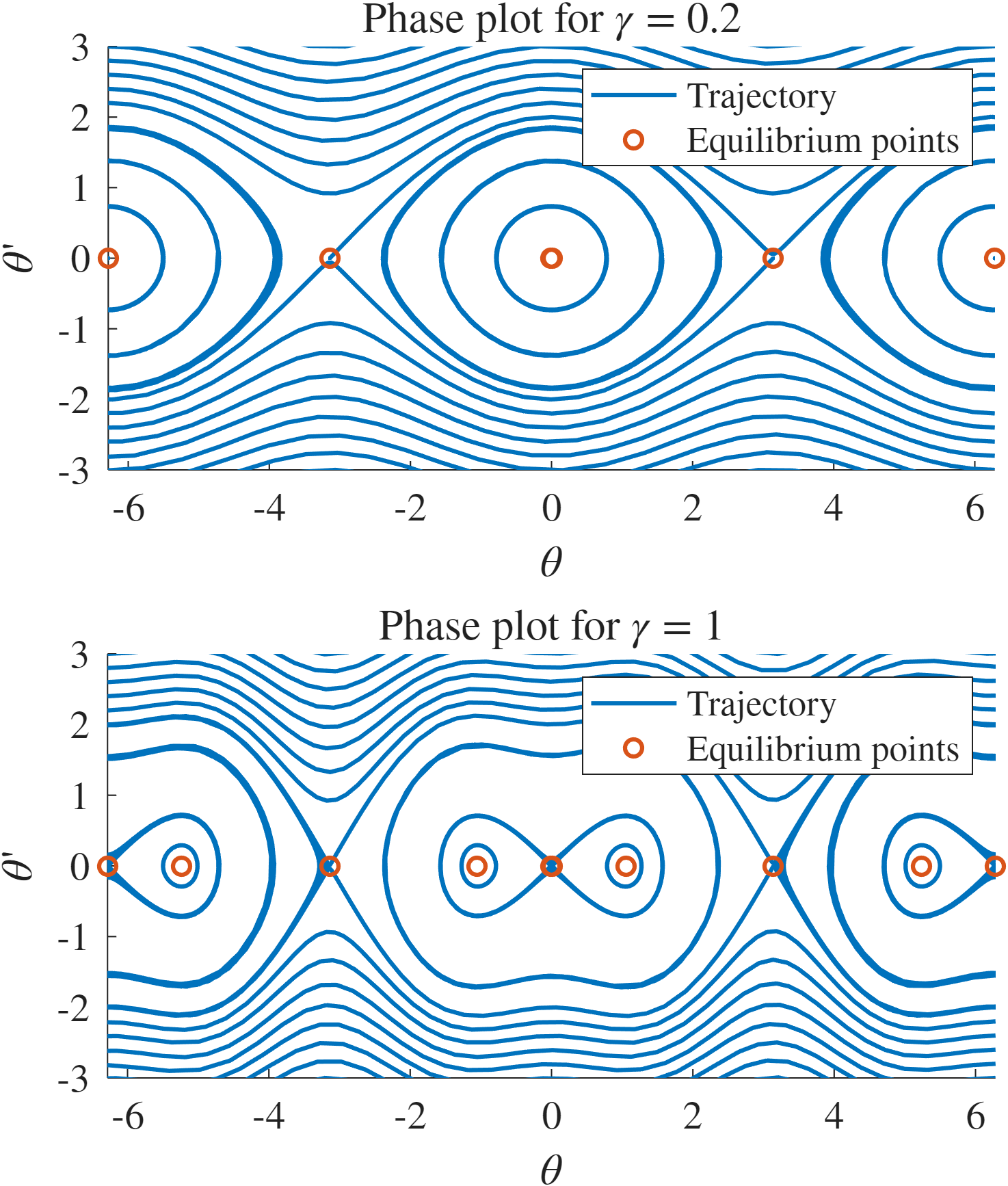
דיאגרמת פאזות עבור ערכי שונים של המערכת.
הקוד נמצא בGitHub.

תרגיל 2

נתון חרוז מאולץ לנוע על מוט ומחובר לשני קפיצים עם אורך חופשי ושני מרסנים צמיגיים סימטרית:

סכמת הבעיה.

סעיף א’

מצא את משוואות התנועה של המערכת.

פתרון:
נשים לב כי כל הכוחות סימטריים יחסית ל- ולכן מסכום כוחות פשוט:

כאשר האורך הוא:

וגם:

נציב ונקבל את משוואת התנועה:

סעיף ב’

נרמל את משוואות התנועה.

פתרון:
נגדיר קבועים אל-ממדיים:

• תדירות עצמית של המערכת - .
• זמן מנורמל, הזמן להשלמת מחזור - .
• יחס הממדים הגאומטריים של המערכת - .
• יחס כבידה לקשיחות המערכת .

בנוסף, לנוחיות:

נקבל:

מכלל השרשרת:

ולכן:

סעיף ג’

מצא נקודות שיווי משקל של המערכת ובצע לינאריזציה.

פתרון:
את משוואת התנועה אנו יכולים לרשום באופן:

כאשר את צד ימין אנו מסמנים בפונקציה .

נאפס את הנגזרות לפי משתנה הזמן המנורמל, כלומר, , ונקבל:

נפתור נומרית (MATLAB). נקבל שאחת מנקודות השיווי משקל היא ולכן נבצע לינאריזציה סביבה:

לכן המשוואה הלינארית היא פשוט:

הערכים העצמיים:

עבור נקבל .
עבור נקבל .

סעיף ד’

חקור את תגובת המערכת ומצא את מעטפת התגובה.

פתרון:
משוואת התנועה שלנו:

מפני שהריסון לא לינארי לא ניתן לחשב פתרון אנליטי מדויק של התגובה. לכן נבצע מספר הנחות ונבטא את מעטפת התגובה בעזרת שיטת האיזון האנרגטי.

נניח כי:

• בהזנחת כבידה והנחת קפיץ קצר, כלומר, וגם :
• אמפליטודת התנודות היא קטנה - , ולכן:
• ניתן לקרב את התגובה המרוסנת של המערכת באמצעות פונקציה סינוסואידית:
• תדירות המערכת המרוסנת היא בקירוב תדירות המערכת הלא מרוסנת, .
• אמפליטודת התנודות דועכת לאט - , כאשר הוא זמן מחזור ( עבור period). מה שאומר:

כעת יש לנו:

נסמן את כוח הריסון ב- ( עבור damped):

לפי שיטת האיזון האנרגטי, העבודה שמבצע כוח הדיסיפציה במחזור אחד שווה לאיבוד האנרגיה הקינטית במחזור אחד. נחשב את עבודת כוח הדיסיפציה במחזור אחד, כלומר בין ל- שגם הוא בעצמו שיא:

נציב את צורת הפתרון שהנחנו:

מאחר ואנו מבצעים אינטגרציה על פונקציה מחזורית בזמן מחזור, לפאזה אין השפעה על האינטגרל, כך שנוכל ל”התעלם” ממנה:

מפני שאמפליטודת התנודות דועכת לאט נוכל להוציא אותה מתוך האינטגרל:

כעת נחשב את האנרגיה הפוטנציאלית בתחילת ובסוף המחזור. בהנחה ויש נקודת קיצון ב- כללי, האנרגיה הפוטנציאלית:

נשים לב שמפני שהמערכת מנורמלת מתקבל ביטוי שתלוי באופן פשוט באמפליטודה.
נפתח את האנרגיה הפוטנציאלית לאחר זמן מחזור בטור טיילור:

הפרש האנרגיות המתקבל:

כאשר הזנחנו ביטויים של נגזרת ממעלה שנייה ומעלה.
השינוי באנרגיה הפוטנציאלית הוא כתוצאה מעבודת הכוח הבלתי משמר. כלומר, :

פתרון המשוואה הדיפרנציאלית יניב את מעטפת הדעיכה:

כאשר את ניתן למצוא מתנאי התחלה.

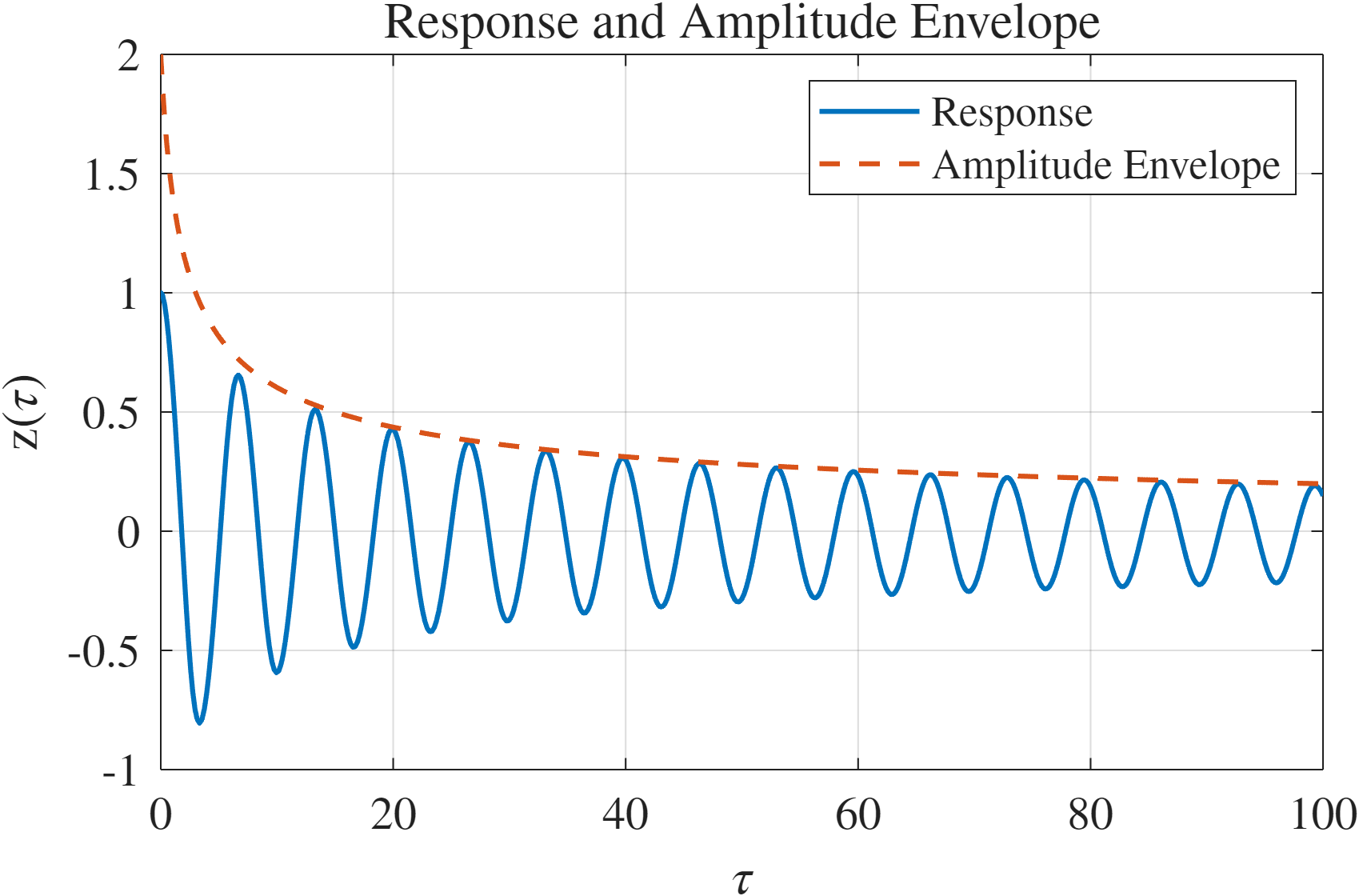
מעטפת הדעיכה עבור , .

הקוד נמצא בGitHub.

→ קודם: DVI1_001הבא: DVI1_003 ←